电子技术——数字逻辑反相器

在学习完如何通过CMOS数字电路实现组合逻辑，接下来我们评估这种数字CMOS电路的性能。首先，我们考虑最基本的部件——反相器。

电压传导特性

下图是一个反相器的原理图：

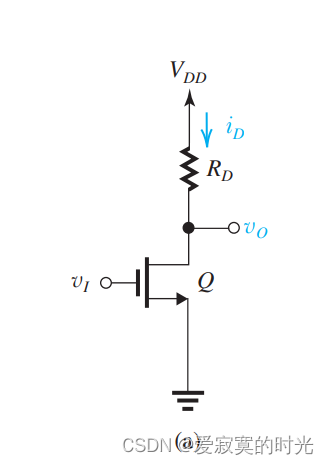
在之前，我们已经介绍了MOSFET的电压传导特性，回忆一下，当输入逻辑0的时候，此时 vI=0v_I = 0vI​=0 小于MOS的阈值电压 VtnV_{tn}Vtn​ 因此MOS管截止（A点），此时 vO=VDDv_O = V_{DD}vO​=VDD​ 输出逻辑1。当输入逻辑1的时候，也就是 vI=VDDv_I = V_{DD}vI​=VDD​ MOS管进入三极管区（D点），输出逻辑0。数字逻辑反相器不想信号放大器，数字逻辑反相器使用MOSFET的非线性区，如图：

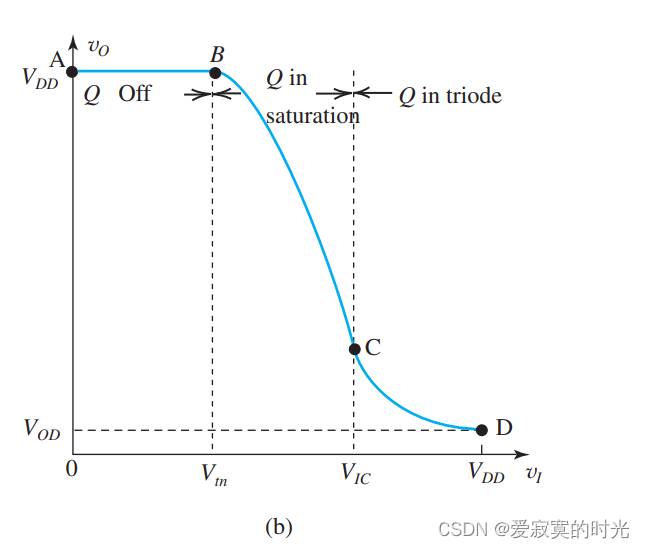
为此，我们可以简化这个模型，如图：

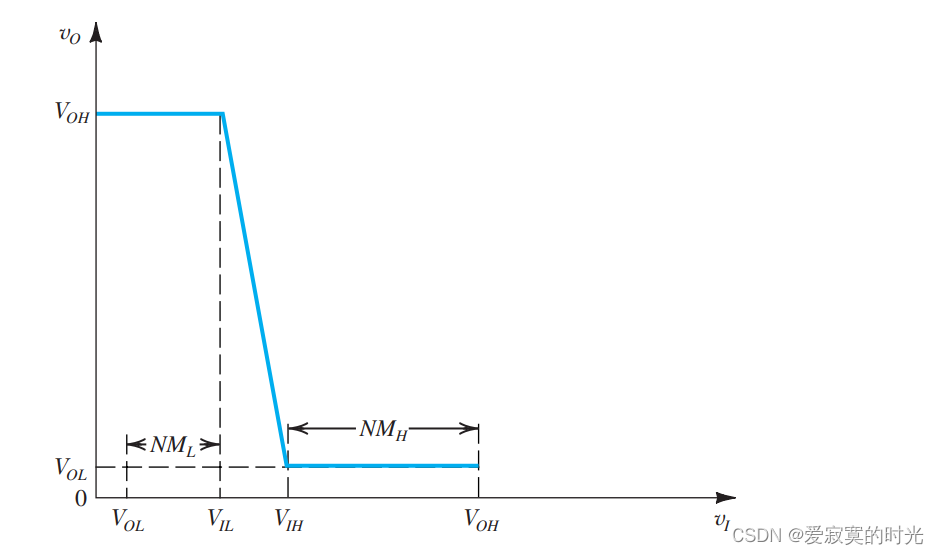
上图中，数字MOS输出的最高电压我们记为 VOHV_{OH}VOH​ 当 vIVILv_I > V_{IL}vI​>VIL​ 的时候，此时数字MOS进入饱和区，在数字MOS中，称为 过渡区 。其中 VILV_{IL}VIL​ 是数字MOS的一个特别重要的参数：它决定了输入 vIv_IvI​ 能够被解释成逻辑0的最大电压值。

同样的，我们观察数字MOS的输出电压最低值 VOLV_{OL}VOL​ 当 vI>VIHv_I > V_{IH}vI​>VIH​ 的时候不依赖于 vIv_IvI​ 。其中 VIHV_{IH}VIH​ 也是数字MOS的一个特别重要的参数：它决定了输入 vIv_IvI​ 能够被解释成逻辑1的最小电压值。

噪声容限

通过上述分析，我们知道，MOS判断逻辑0还是1存在一定的容限区间，这也是对于模拟电路来说数字电路的优点之一。为了量化这种容限性质，考虑下图的一种情况，后面的反相器被前面的反相器所驱动：

这里，我们假设在 G1G_1G1​ 和 G2G_2G2​ 之间存在噪声 vNv_NvN​ ，即：

vI2=vO1+vNv_{I2} = v_{O1} + v_N vI2​=vO1​+vN​

接下来，考虑 vO1=VOLv_{O1} = V_{OL}vO1​=VOL​ 此时 G2G_2G2​ 的输入是逻辑0，我们发现，只要 vI2v_{I2}vI2​ 不超过 VILV_{IL}VIL​ 那么逻辑就不会发生改变，因此 vNv_NvN​ 的最大值可以是 VIL−VOLV_{IL} - V_{OL}VIL​−VOL​ ，我们称 G2G_2G2​ 对于 低电压输入有噪声容限 记为：

NML=VIL−VOLNM_L = V_{IL} - V_{OL} NML​=VIL​−VOL​

同样的，若 vO1=VOHv_{O1} = V_{OH}vO1​=VOH​ ，我们发现，只要 vI2v_{I2}vI2​ 不小于 VIHV_{IH}VIH​ 那么逻辑就不会发生改变，因此 vNv_NvN​ 的最小值可以是 VOH−VIHV_{OH} - V_{IH}VOH​−VIH​ ，我们称 G2G_2G2​ 对于 高电压输入有噪声容限 记为：

NMH=VOH−VIHNM_H = V_{OH} - V_{IH} NMH​=VOH​−VIH​

总之，数字MOS的 VOL,VIL,VOH,VIHV_{OL},V_{IL},V_{OH},V_{IH}VOL​,VIL​,VOH​,VIH​ 参数决定了数字MOS的传导特性，以及噪声容限。换句话说，噪声引起的在噪声容限内的电压改变被数字MOS所拒绝，而且数字MOS又将受噪声影响的电平值恢复成原始电平值继续传播，这也是为什么数字电路在信号质量上优于模拟电路的原因。下表总结了数字MOS的参数：

下图给出了 VILV_{IL}VIL​ 和 VIHV_{IH}VIH​ 的形式化定义：

我们发现 VILV_{IL}VIL​ 和 VIHV_{IH}VIH​ 被定义在曲线斜率为-1的拐点处。除此之外，我们还定义了曲线中点M，在中点M出输出电压等于输入电压。点M可以粗略的看做是数字MOS从一个状态切换为另一个状态。

理想电压传导

什么是理想的反相器电压传导？通过刚才的分析我们知道，一个理想的反相器电压传导应该具有最大的电压摆幅以及噪声容限，对于一个电源电压为 VDDV_{DD}VDD​ 的反相器来说，获得最大的电压摆幅当：

VOH=VDDV_{OH} = V_{DD} VOH​=VDD​

VOL=0V_{OL} = 0 VOL​=0

为了获得最大的噪声容限，则过渡区的宽度越小越好，理想情况下则是零宽度，而且高低电压区各占一半，如图：

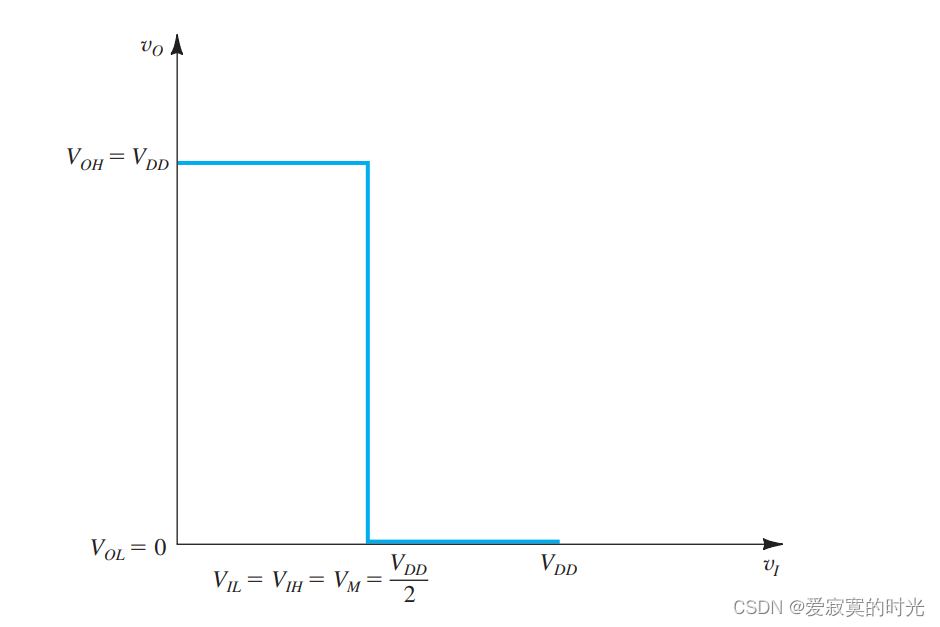
我们有：

VIL=VIH=VM=VDD/2V_{IL} = V_{IH} = V_M = V_{DD}/2 VIL​=VIH​=VM​=VDD​/2

反相器实现

使用晶体管实现的反相器我们称为 压控开关 。最简单的反相器实现如下图：

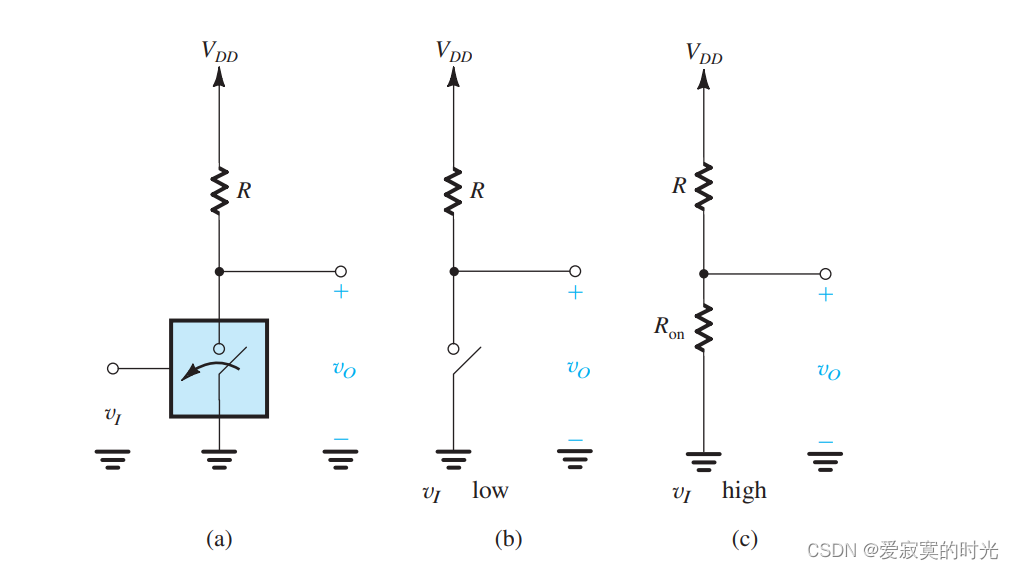
这个开关受到电压 vIv_IvI​ 控制。当 vIv_IvI​ 是低电压的时候，开关打开，此时没有电流通过 RRR ，此时 vO=VDDv_O = V_{DD}vO​=VDD​ 。当 vIv_IvI​ 是高电压的时候，开关闭合，假设开关是理想的，此时输出 vO=0v_O = 0vO​=0 。

晶体管开关，例如MOS和BJT开关，并不是理想开关，尽管 开路电阻 是非常高的，可以近似看成是开路，但是 闭合电阻 是有限的 RonR_{on}Ron​ 。这就造成了当晶体管开关闭合的时候，等价于上图的©电路，此时输出电压为：

VOL=VDDRonR+RonV_{OL} = V_{DD} \frac{R_{on}}{R + R_{on}} VOL​=VDD​R+Ron​Ron​​

另外一种更高级的反相器实现如下图：

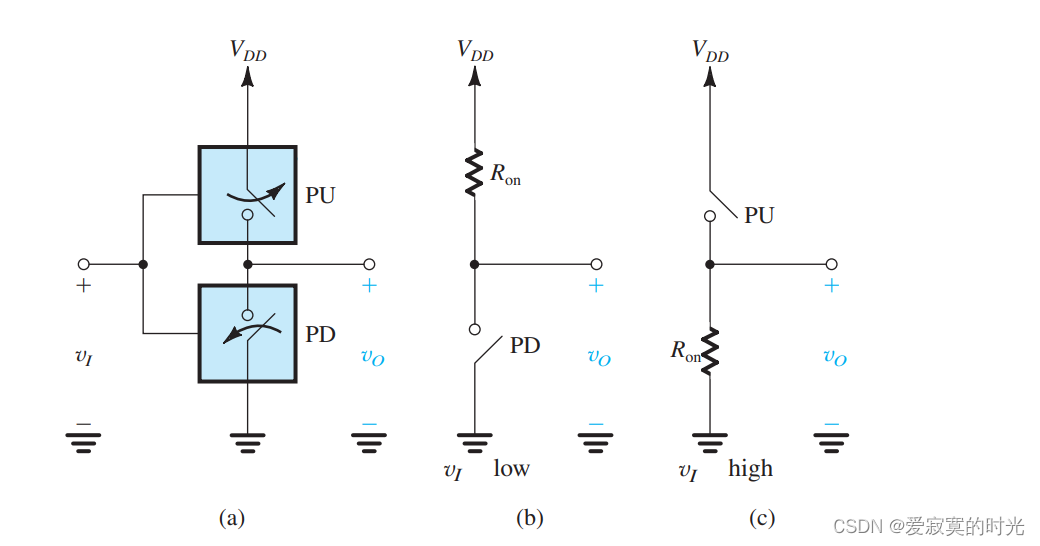
上图我们使用了 互补开关 ，其中 上拉PU开关 负责将输出节点接入 VDDV_{DD}VDD​ ，下拉PD开关 负责将输出节点接入地。当 vIv_IvI​ 低电压输入的时候，PU闭合而PD打开，如图(b)，此时输出 vO=VDDv_O = V_{DD}vO​=VDD​ ，因此 vOH=VDDv_{OH} = V_{DD}vOH​=VDD​ 。同样的，若 vIv_IvI​ 输入高电平的时候，此时PU断开而PD闭合，输出 vO=0v_{O} = 0vO​=0 。观察到该电路中没有电流流过，因此耗散功率为零。这个电路的优势比起使用单下拉开关加上 上拉电阻 来说，具有最大的电压摆幅和零耗散功率。这也是我们之前说的上拉下拉网络的实现。

最后，考虑另外一个反相器实现：

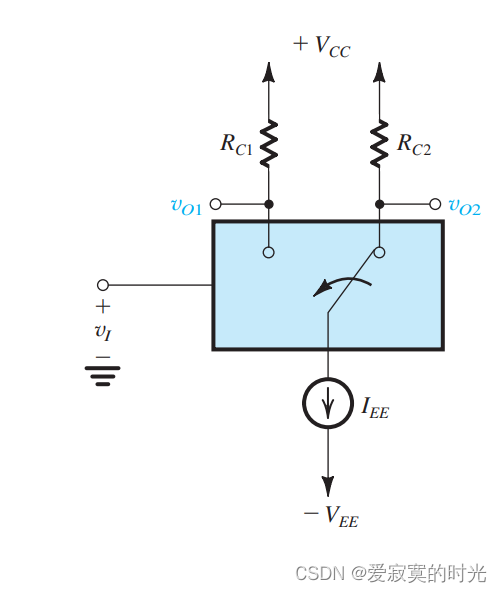
这里由一个双掷开关和一个公共电流源实现，当输入高低电平的时候，开关在两个状态下转换，因为电流是固定的，所以输出值取决于电阻 RC1R_{C1}RC1​ 和 RC2R_{C2}RC2​ 的值，并且输出电压与开关的阻抗无关，他是实现快速逻辑电路的基础，称为发射极耦合逻辑ECL。