【FMCW 04】测角-Angle FFT
在之前的文章中,我们已经详尽讨论过FMCW雷达测距和测速的原理,现在来讲最后一块内容,测角。测角对于硬件设备具有要求,即要求雷达具有多发多收结构,从而形成多个空间信道(channel),我们正是利用这些channel间的差异性来完成对目标的测角。
本节讲述通用的Angle FFT测角的原理。
天线阵列
在一个具有多发多收的天线结构中,我们可以得到一个天线阵列(array)。一个Tx-Rx就构成了一个空间信道。
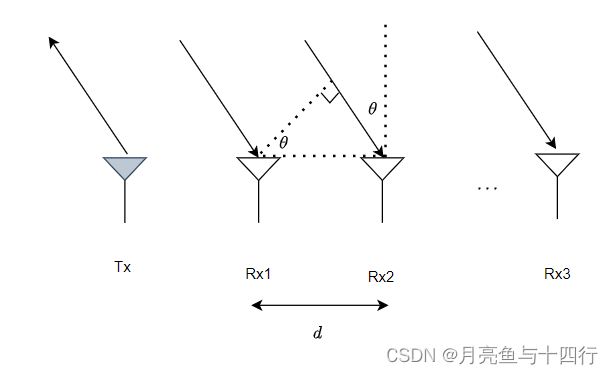
设相邻的两个天线之间排布间距为ddd,到达角(angle of arrival,AoA)为 θ\thetaθ,则相邻的两个天线之间会产生一个固定的光程差 dsinθd \sin \thetadsinθ,这个固定的光程差会造成相邻两个信道间接收回波固定的相位差。即
dsinθλ=Δϕ2π\frac{d \sin \theta}{\lambda}=\frac{\Delta \phi}{2\pi} λdsinθ=2πΔϕ
于是我们就有
sinθ=λ2πdΔϕ\sin\theta = \frac{\lambda}{2 \pi d} \Delta \phi sinθ=2πdλΔϕ
最大测量角度
由于 取天线阵列间距为λ2\frac{\lambda}{2}2λ时,就可得此时测量达到达到角的范围正好在±90°,即 −1 但值得注意的是,虽然sinθ\sin \thetasinθ与我们的Δϕ\Delta \phiΔϕ成正比,但由于sinθ\sin \thetasinθ 函数本身的非线性,θ\thetaθ 在角度小时对Δϕ\Delta \phiΔϕ更敏感,或者说:在低角度范围(如AoA±30°)内测角的精度(或区分度)更高。 可以看下面的函数图来有一个直观的认识:当我们在sinθ\sin \thetasinθ轴取均匀标度,在θ\thetaθ 轴上的标度随角度的增加是越来越粗的。 在之前 测速 的文章中,我们已经讨论过相位差的周期性,及其基于数字域角分辨率下的FFT结果。那么,现在由于N个信道所造成的固定相位差,同样也会形成这个一个相位差的周期性。 借用一幅TI教程的示意图,我们此时对在同一range bin中且又在同一 velocity bin中的两个运动物体进行区分,那么,如果其AoA不同,我们就可以借由 angle FFT 来完成对这两个运动物体的区分。 看得出来,此处的推导与测速中的推导相近。在数字域上的角速度分辨率为 根据导数的定义,我们有 如果取天线阵列间距为 λ2\frac{\lambda}{2}2λ ,且设 θ=0\theta = 0θ=0,就可以得到通常定义下的最精细的角度分辨率为
−π<Δϕ<π-\pi<\Delta \phi < \pi −π<Δϕ<π
所以最大测量角度为
θmax
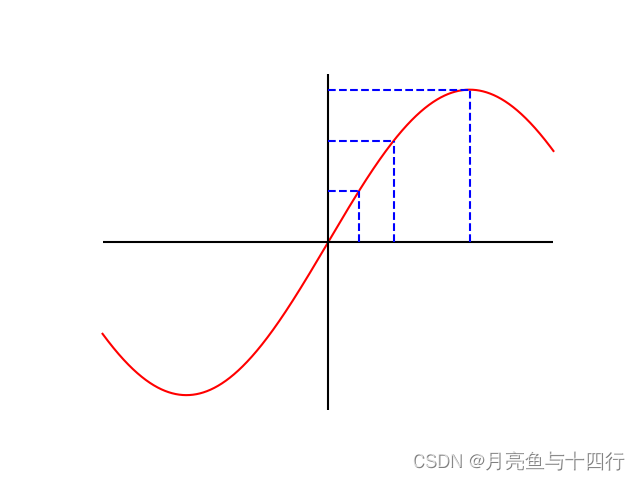
相位差的周期性

角度分辨率
Δω=2πNradians/sampleΔω= \frac{2 \pi}{N} radians/sample Δω=N2πradians/sample
其中N为FFT的点数,继续令Δϕ=w\Delta \phi = wΔϕ=w,则
sin(θ+Δθ)−sin(θ)=λ2πd(Δw+w)−λ2πdw=λ2πdΔw\sin(\theta + \Delta \theta) -\sin(\theta) = \frac{\lambda}{2 \pi d}(\Delta w +w) - \frac{\lambda}{2 \pi d}w = \frac{\lambda}{2 \pi d}\Delta w sin(θ+Δθ)−sin(θ)=2πdλ(Δw+w)−2πdλw=2πdλΔw
sin(θ+Δθ)−sin(θ)Δθ=cosθ\frac{ \sin(\theta + \Delta \theta) -\sin(\theta) }{\Delta \theta}= \cos \theta Δθsin(θ+Δθ)−sin(θ)=cosθ
于是,可进一步推得
cos(θ)Δθ=λ2πdΔw\cos (\theta) \Delta \theta = \frac{\lambda}{2 \pi d}\Delta w cos(θ)Δθ=2πdλΔw
Δθ=λ2πdcos(θ)Δw=λNdcos(θ)\Delta \theta = \frac{\lambda}{2 \pi d \cos (\theta) }\Delta w=\frac{\lambda}{N d \cos (\theta) } Δθ=2πdcos(θ)λΔw=Ndcos(θ)λ
这里同样可对之前低角度范围内测角的精度(或区分度)更高的原因做出解释:cosθ\cos \thetacosθ在低角度时值更大,使得此时的 Δθ\Delta \thetaΔθ 有着更细微的取值。
θres=2N\theta_{res} = \frac{2}{N} θres=N2
可见其将受限于能够完成多发多收的天线数量。