第八章.贝叶斯分析—贝叶斯定理朴素贝叶斯
第八章.贝叶斯分析
8.1 贝叶斯定理&朴素贝叶斯
贝叶斯主要应用与新闻分类,文本分类,评论分析。
1.数理统计学处理的信息
1).贝叶斯方法
- 关于统计推断的系统理论和方法,称为贝叶斯方法。
2).经典统计学
-
总体信息:当前总体样本符合某种分布,比如0-1分布,二项分布,正态分布。
-
样本信息:通过抽样得到的部分样本的某种分布
-
抽样信息=总体信息+样本信息
-
基于抽样信息进行统计推断的理论和方法称为经典统计学
3).贝叶斯统计学
-
先验信息:抽样之前,有关推断问题中未知参数的一些信息,通常来自与经验或历史资料。
-
基于总体信息+样本信息+先验信息进行统计推断的方法和理论,称为贝叶斯统计学。
2.贝叶斯定理
1).贝叶斯定理交换概率中的条件和结果的公式:
-
如果已知P(X|H),求P(H|X):

-
参数解析:
①.P(H|X)给定观测数据样本X,假设H是成立的概率. [比如X是一份具有特定特征的邮件,H是垃圾邮件,它里面包含很多的单词(特征),然后我们判断这封邮件属于垃圾邮件的概率是多少]②.P(H|X)是后验概率 [比如一份特定邮件中,是垃圾邮件的概率]
③.P(H)是H的先验概率 [比如总体邮件中垃圾邮件的概率]
④.P(X)是X的先验概率 [比如总体邮件中带有特定特征的邮件概率]
-
大数定理:
可以通过抽样来计算先验概率。抽样的数量越大,得到的结果越接近于真实的概率分布。
2).示例1:以邮件是否为垃圾邮件为例

-
描述
①.P(H):垃圾邮件的先验概率②.P(X):特定特征的先验概率
③.P(X|H):在垃圾邮件中,包含特定特征(比如“办证”)邮件的概率
④.P(H|X):包含特定特征(比如“办证”)的邮件属于垃圾邮件的概率
-
有一个特定特征的情况:
①.邮件:总体100,正常70,垃圾30,“办证”’在正常邮件中出现10次,在垃圾邮件中出现25次。②.假设X为“办证”,H为垃圾邮件。
· P(X|H)=25/30=5/6
· P(H)=30/100=3/10
· P(X)=35/100=7/20
· P(H|X)=5/7③.包含“办证”这个词的邮件属于垃圾邮件的概率为5/7。
-
有多个特定特征的情况:
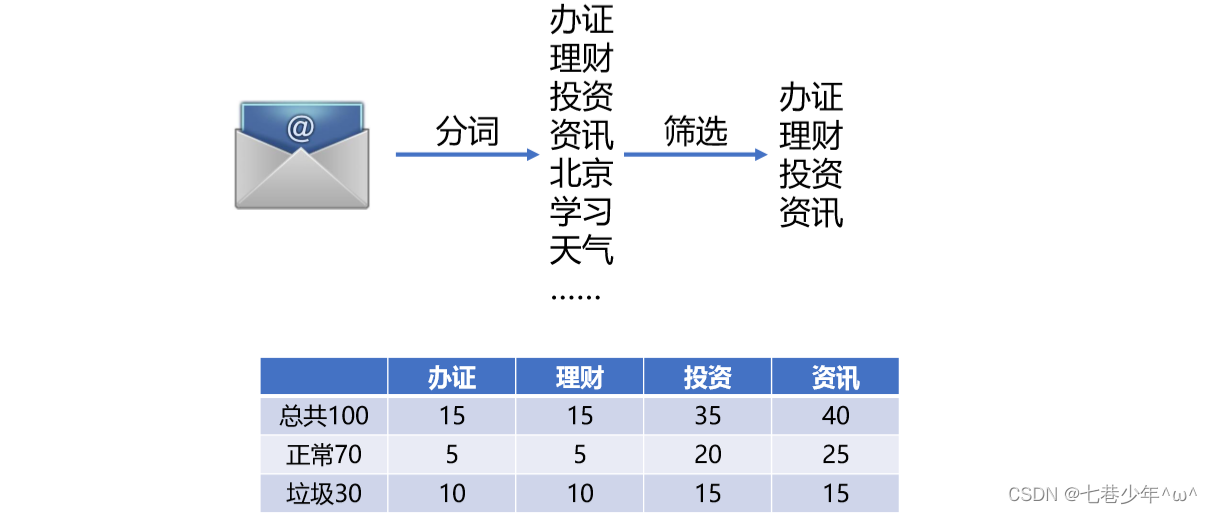
①.在有多个特征的情况下会使得统计量巨大。②.比如需要计算办证对于垃圾邮件的影响
③.计算办证+理财对于垃圾邮件的影响 计算办证+理财+投资对于垃圾邮件的影响
④.计算办证+理财+投资+资讯对于垃圾邮件的影响
⑤.……
⑥.所有特征需要计算2n-1次,n是特征数
3.朴素贝叶斯 (Naive Bayes)
有多个特定特征的情况下,若继续使用上述公式,计算将会变得很复杂,故可以使用朴素贝叶斯。
1).公式
- 假设:特征X1,X2,X3……之间都是相互独立的
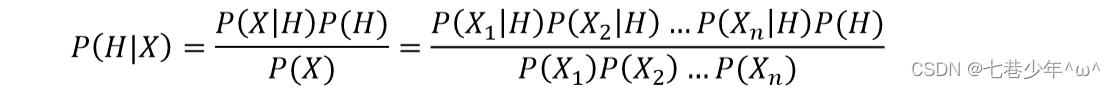
2).常见的朴素贝叶斯模型
①.多项式模型(MultinomialNB)
-
以垃圾邮件分类为例:
1).特定特征:“代开发票”,“增值税发票”,“正规发票”
2).分词后为向量:(“代开”,“发票”,“增值税”,“发票”,“正规”,“发票”)
3).重复的词语我们视为其多次出现:
4).计算:

②.伯努利模型(BernoulliNB)
-
以垃圾邮件分类为例
1).特定特征:“代开发票”,“增值税发票”,“正规发票”
2).分词后为向量:(“代开”,“发票”,“增值税”,“发票”,“正规”,“发票”)
3).重复的词语我们视为其出现一次:
4).计算:

③.混合模型
- 在计算句子概率时,不考虑重复词语出现的次数,但是在统计计算词语的概率P(“词语”|S)时,却考虑重复词语的出现次数,这种模型叫做混合模型。
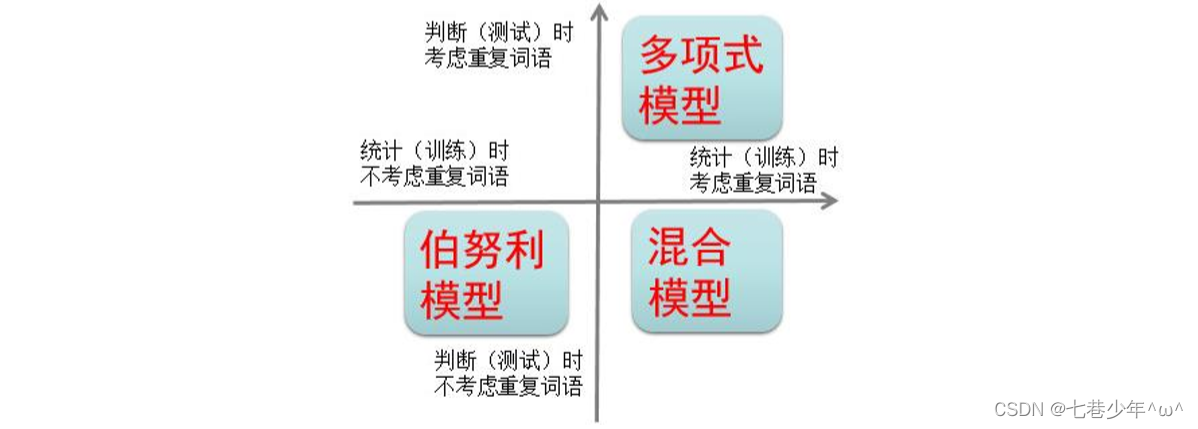
④.高斯模型 (GaussianNB)
- 有些特征可能是连续型变量,比如说人的身高,物体的长度,这些特征可以转换成离散型的值.
- 比如身高在160cm以下,特征值为1;在160cm和170cm之间,特征 值为2;在170cm之上,特征值为3。
- 也可以这样转换, 将身高转换为3个特征,分别是f1、f2、f3,如果身高是 160cm以下,这三个特征的值分别是1、0、0,若身高在 170cm之上,这三个特征的值分别是0、0、1。不过这些 方式都不够细腻,高斯模型可以解决这个问题。
⑤.词袋模型 (Bag of Words)
1).概念:
Bag-of-words model (BoW model)最早出现在自然语言处理(Natural Language Processing)和信息检索 (Information Retrieval)领域。该模型忽略掉文本的语 法和语序等要素,将其仅仅看作是若干个词汇的集合,文档中每个单词的出现都是独立的。BoW使用一组无序的 单词(words)来表达一段文字或一个文档。
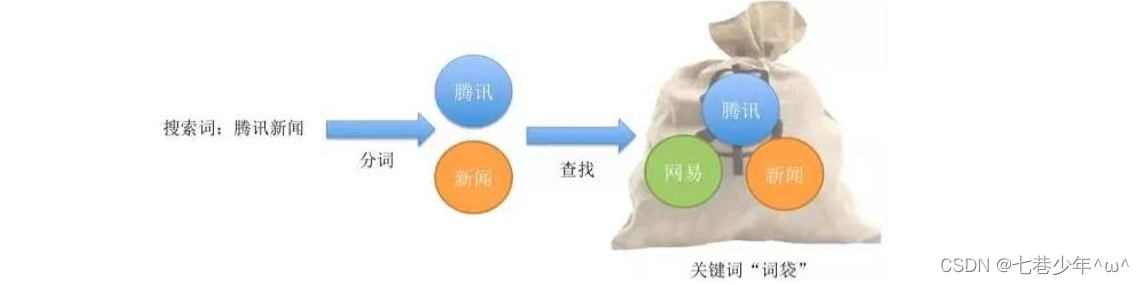
2).示例:
①.首先给出两个简单的文本文档.

②.基于上述两个文档中出现的单词,构建一个词典:
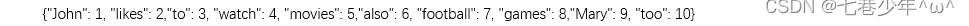
③.上面的词典中包含10个单词, 每个单词有唯一的索引,那么每个文本我们可以使用一个10维的向量来表示。如下:
·[1, 2, 1, 1, 1, 0, 0, 0, 1, 1]
·[1, 1,1, 1, 0, 1, 1, 1, 0, 0 ]
④.注意:该向量与原来文本中单词出现的顺序没有关系,而是词典中每个单词在 文本中出现的频率。
4.示例1—贝叶斯(iris)
1).代码实现
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.naive_bayes import MultinomialNB, BernoulliNB, GaussianNB# 加载数据
iris = load_iris()
x_data = iris.data
y_data = iris.target# 数据切分
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data)# 创建模型
mul_nb = GaussianNB() # 高斯模型
mul_nb.fit(x_train, y_train)# 预测函数
prediction = mul_nb.predict(x_test)print(classification_report(y_test, prediction))
print(confusion_matrix(y_test, prediction))2).结果展示
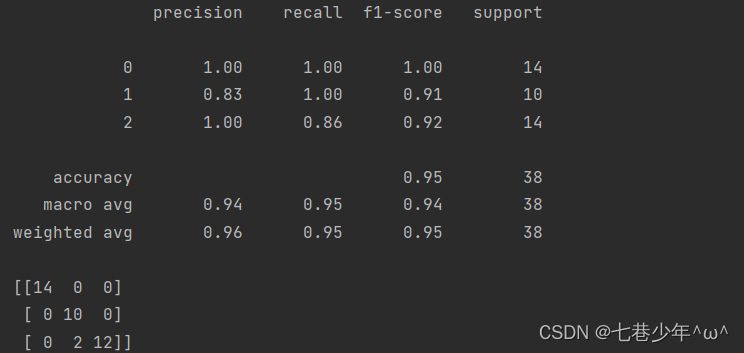
5.示例2—词袋模型构建单词的字典
1).代码实现
from sklearn.feature_extraction.text import CountVectorizertexts = ['dog cat fish', 'dog cat cat', 'fish bird', 'bird']
cv = CountVectorizer()
cv_fit = cv.fit_transform(texts)print(cv.get_feature_names_out())
print(cv_fit.toarray())
print(cv_fit.toarray().sum(axis=0))2).结果展示
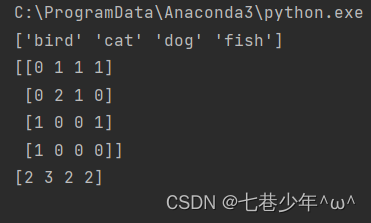
6.TF_IDF算法 —自然语言处理中比较重要的算法
提取词频(Term Frequency,缩写TF),
1).TF_IDF算法的思想:
-
假设我们把停用词都过滤掉了,只考虑有意义的词。可能会遇到 这样一个问题,“中国”,“蜜蜂”,“养殖”这三个词的TF一样。 作为关键词,它们的重要性是一样的吗?
-
用统计学语言表达,就是在词频的基础上,要对每个词分配 一个"重要性"权重。最常见的词(“的”、“是”、“在”)给予 最小的权重,较常见的词(“中国”)给予较小的权重,较少 见的词(“蜜蜂”、“养殖”)给予较大的权重。这个权重叫做 “逆文档频率”(Inverse Document Frequency,缩写为 IDF),它的大小与一个词的常见程度成反比。
2).常见计算词频(TF)的方法:

3).计算逆文档(IDF)频率的方法:

4).TF_IDF的计算公式:
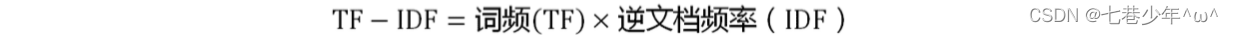
5).公式示例分析
· 题干:
以《中国的蜜蜂养殖》为例,假定该文长度为1000个词, “中国”、“蜜蜂”、“养殖"各出现20次,则这三个词的"词频” (TF)都为0.02。然后,搜索Google发现,包含"的"字的网页 共有250亿张,假定这就是中文网页总数。包含"中国"的网页共 有62.3亿张,包含"蜜蜂"的网页为0.484亿张,包含"养殖"的网 页为0.973亿张。则它们的逆文档频率(IDF)和TF-IDF如下:
· 结果:
| 关键词 | 包含该次的文档数(亿) | TF | IDF | TF_IDF |
|---|---|---|---|---|
| 中国 | 62.3 | 0.02 | 0.603 | 0.0121 |
| 蜜蜂 | 0.484 | 0.02 | 2.713 | 0.0543 |
| 养殖 | 0.973 | 0.02 | 2.410 | 0.0482 |
6).示例
· 代码实现:
from sklearn.feature_extraction.text import TfidfVectorizertext = ['The quick brown fox jumped over the lazy dog.', 'The dog.', 'The fox']# 创建变换函数
Tfdif = TfidfVectorizer()
# 词条化以及创建词汇表
Tfdif.fit(text)# 总结
print(Tfdif.vocabulary_)#词的字典
print(Tfdif.idf_)# 编码文档
vector = Tfdif.transform([text[0]])
# 总结编码文档
print(vector.toarray())· 结果展示:
