这节的内容需要一些线性代数基础知识，如果你没听懂本文在讲什么，强烈建议你学习【官方双语/合集】线性代数的本质 - 系列合集

文章目录

• 奇异值分解
• • 线性变换
  • 特征值和特征向量的几何意义
  • 什么是奇异值分解？
  • 公式推导
  • • SVD推广到任意大小矩阵
  • 如何求SVD分解
• 非负矩阵分解（NMF)
• 主成分分析PCA
• • 我们为什么需要PCA？
  • 来找坐标原点
  • 来找坐标系
  • 怎么理解PCA
  • 什么是协方差矩阵
  • • 公式推导
    • 重要思考！
    • 置信椭圆
    • PCA的缺点
  • PCA主成分与SVD的关系

奇异值分解

这段看的视频是【学长小课堂】什么是奇异值分解SVD–SVD如何分解时空矩阵

线性变换

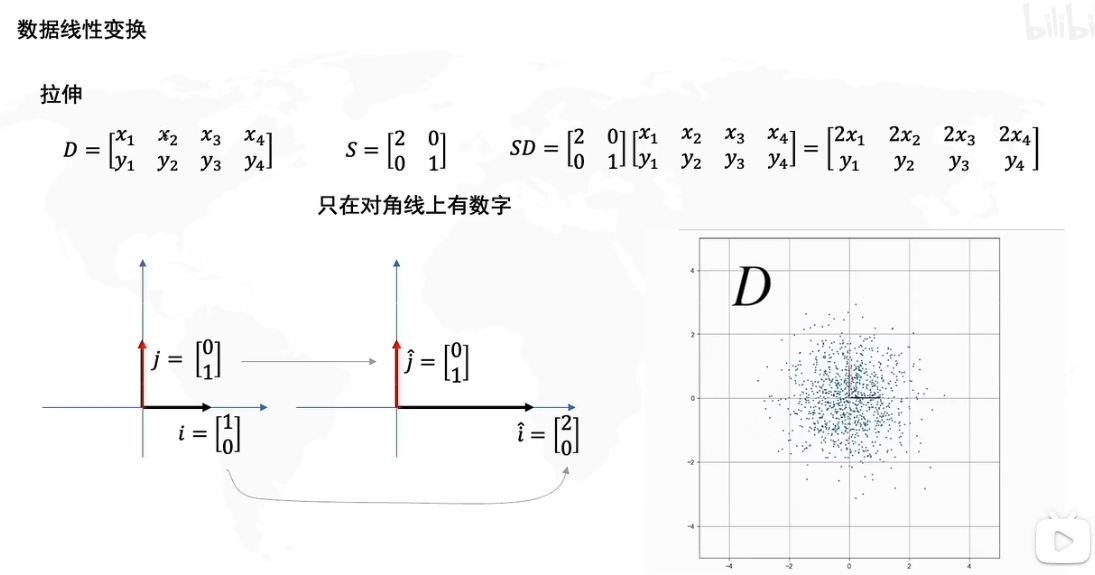
大多数本科生接触的线性代数可能只是矩阵的运算，如果我们从几何意义上来理解会发现一个崭新的世界。

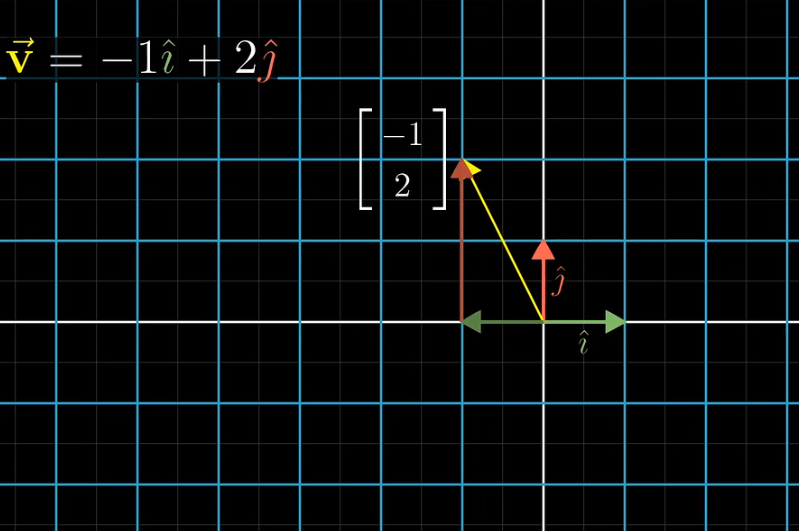
假设我们给出一个原矩阵D，D的矩阵如上所示，D由四个向量[x1,y1]T...[x4,y4]T[x_1,y_1]^T...[x_4,y_4]^T[x1​,y1​]T...[x4​,y4​]T构成。矩阵D的基（基底）是数轴正方形上的单位向量j=[0,1]T,i=[1,0]Tj=[0,1]^T,i=[1,0]^Tj=[0,1]T,i=[1,0]T,如图左所示，实际上任何一个向量我们都可以视作基的运算，如下图。


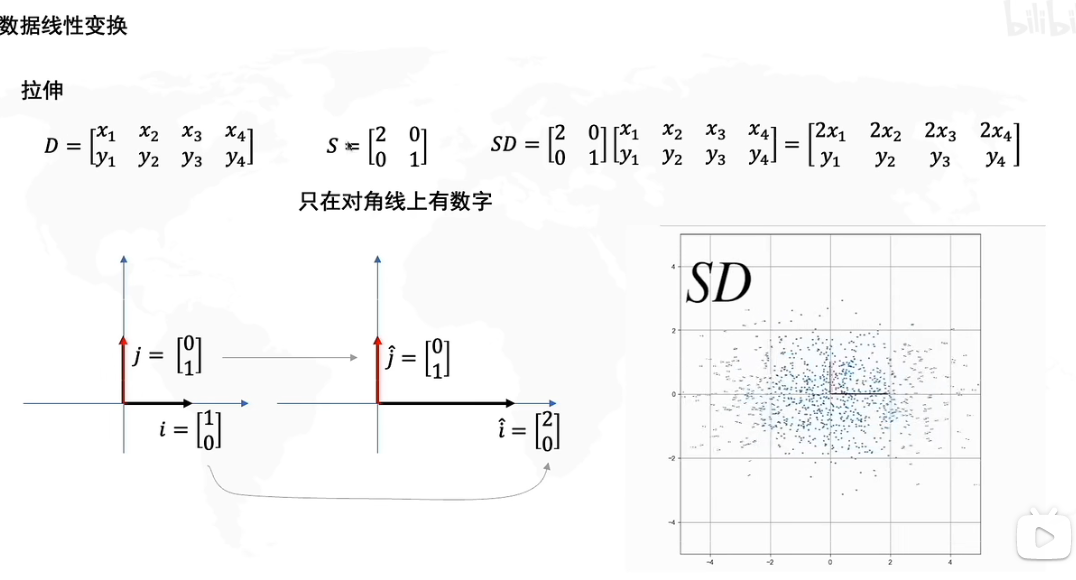
现在我们给出一个矩阵S=[2001]S=\begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix}S=[20​01​]，然后我们将矩阵SD相乘，如果单纯运算我们当然知道SD的结果。现在让我们再看看新矩阵SD，我们会发现其中的向量[2x1,y1]....[2x4,y4][2x_1,y_1]....[2x_4,y_4][2x1​,y1​]....[2x4​,y4​]在x轴上都变为了原来的两倍。
实际上，矩阵运算AB=C，我们可以解读为：对B矩阵应用了A变换从而得到了新矩阵C
我们将D矩阵简写为D=[xy]D=\begin{bmatrix} x\\ y \end{bmatrix}D=[xy​]，也就是说SD=[2001][xy]=x[20]+y[01]SD=\begin{bmatrix} \textcolor{red}{2} & \textcolor{blue}{0} \\ \textcolor{red}{0} & \textcolor{blue}{1} \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}=x\begin{bmatrix} \textcolor{red}{2} \\ \textcolor{red}{0} \end{bmatrix}+y\begin{bmatrix} \textcolor{blue}{0} \\ \textcolor{blue}{1} \end{bmatrix}SD=[20​01​][xy​]=x[20​]+y[01​]
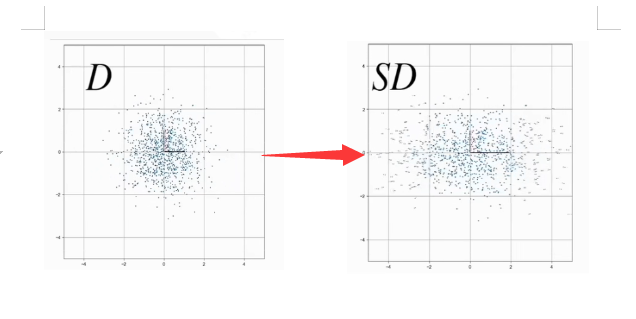
因此S变换相当于将x乘以两倍，y乘以一倍，本质上SSS矩阵对DDD矩阵的基进行了线性变换，j∗1→j^,i∗2→i^j*1 \to \hat j,i*2 \to \hat ij∗1→j^​,i∗2→i^，因此如下图所示，SD会将D横向拉伸两倍。

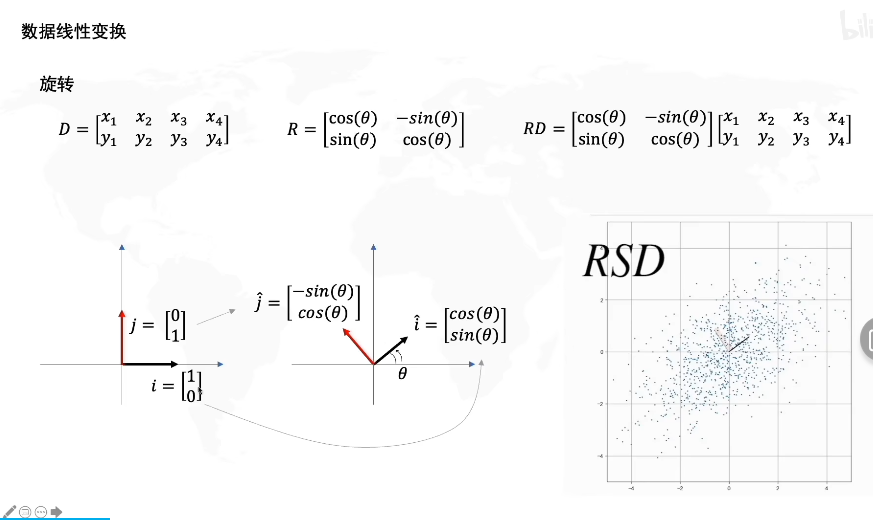
如图我们对矩阵D乘以一个旋转矩阵R，其中R=[cos(θ)−sin(θ)sin(θ)cos(θ)]R=\begin{bmatrix} cos(θ)&-sin(θ) \\ sin(θ) &cos(θ) \end{bmatrix}R=[cos(θ)sin(θ)​−sin(θ)cos(θ)​]，其中θ角代表了旋转的角度，当然这个矩阵代表了整体的旋转，你可以想象整个网格以原点为旋转中心旋转。

矩阵的线性变换就包括拉伸和旋转两种，如果一个矩阵(向量)x在应用了变换矩阵A后，原点位置依旧不变，且基向量为直线，坐标上的网格线保持平行，我们就称这种变换为线性变换。

一种更直观的变换方式，就是将基向量移动到变换矩阵对应的坐标，想象整个网格随之运动。

在乘以R矩阵后，RSD相当于在SD的图像上应用了线性旋转得到了新的图像。

特征值和特征向量的几何意义

矩阵乘法核心思想(6)：特征向量与特征值的几何意义
先说结论，其实我们刚才已经讲过了。

• 矩阵乘法即线性变换——对向量进行旋转和长度伸缩，效果与函数相同;
• 特征向量指向只缩放不旋转的方向;
• 特征值即缩放因子;
• 旋转矩阵无实数特征向量和特征值。
  

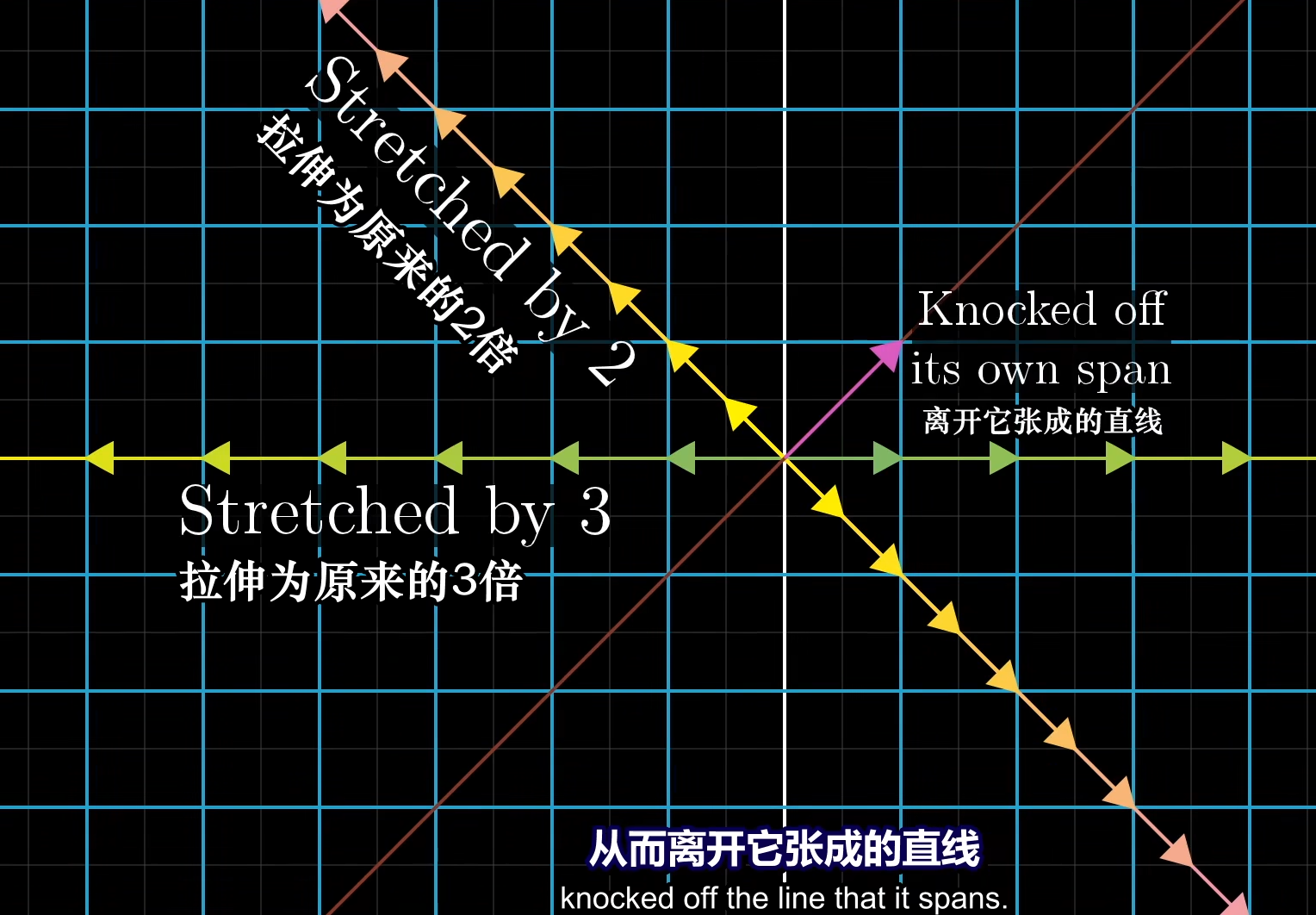
单个向量的张成空间是一条直线，在大部分时候，线性变换后的向量会偏移原来的张成空间，然而某些时候一些向量仅仅只是将进行了拉伸，因此就被留在了原张成空间中，或者说所有处于这条直线上的向量都仅仅只是被拉伸。我们把这些应用了线性变换后仍然留在原张成空间的向量称为特征向量，其被拉伸的比例因子我们称为特征值，因此，拉伸为三倍的那个直线就是一个属于特征值3的特征向量。

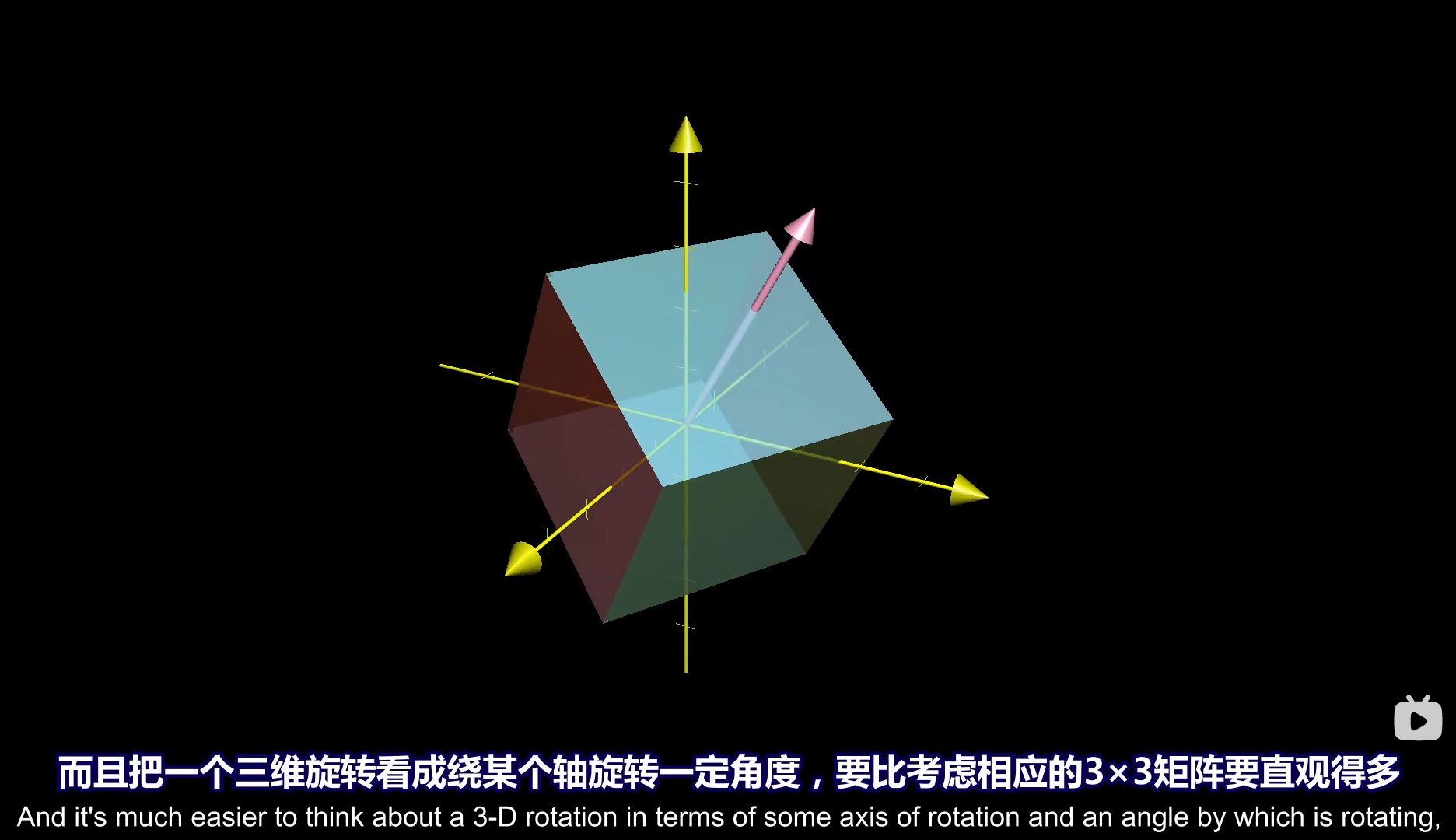
那么假设我们找到了这个特征向量，然后对一个三维矩阵（我们将其看作一个三维空间）进行了一次旋转，我们知道特征向量经过旋转这种线性变换仍然留在原张成空间上，因此特征向量线性变换前后的位置保持不变，那么我们就可以视为对这个矩阵以特征向量为旋转轴进行了一次旋转。

计算特征值的公式就是AV⃗=λV⃗A\vec V=\lambda \vec VAV=λV,其中λ\lambdaλ是特征值矩阵，寻找特征向量V⃗\vec VV就是求解(A−λE)V⃗=0(A-\lambda E)\vec V=0(A−λE)V=0,这是一个齐次线性方程组，当det(A−λE)=0det(A-\lambda E)=0det(A−λE)=0或(A−λE)(A-\lambda E)(A−λE)这个矩阵非满秩的时候存在非零解。

现在让我们重新审视一下AV⃗=λv⃗A\vec V=\lambda \vec vAV=λv这个式子：

A代表了一个变换矩阵，v⃗\vec vv代表了特征向量，当矩阵*向量=向量，因此Av⃗A\vec vAv代表了对v⃗\vec vv的一次线性变换，在SVD中，我们可以将矩阵变换拆解为A=DRA=DRA=DR，即旋转和拉伸，因此Av⃗A\vec vAv相当于对向量v⃗\vec vv进行了旋转加拉伸的线性变换，它的结果AV⃗=λv⃗A\vec V=\lambda \vec vAV=λv,相当于对原向量拉伸了特征值λ\lambdaλ倍。也就是说，在特征向量上的线性变换A完全可以由λ\lambdaλ所定义！

那么特征值能不能是复数呢？能，这意味着特征向量缩放了一个虚数倍？在笛卡尔坐标系上实在是太难想象了，而且有些超纲了。

为什么对角矩阵的主元就是特征值？我们可以将基向量视为特征向量，因此主元上的元素就是特征值。

我们能进行SVD分解的基础之一就是特征值的这些特性，实际上SVD公式M=UΣVTM=U\Sigma V^TM=UΣVT中的U,V都代表旋转变换，只有Σ\SigmaΣ代表了缩放，而在后面我们也会知道，原来MMTMM^TMMT的特征值L=Σ2L=\Sigma^2L=Σ2，如果我们对一个非奇异矩阵进行了SVD分解，所得到的奇异值其实就是特征值，因此和我们现在所说的特征值代表缩放因子这一结论是一致的。

什么是奇异值分解？

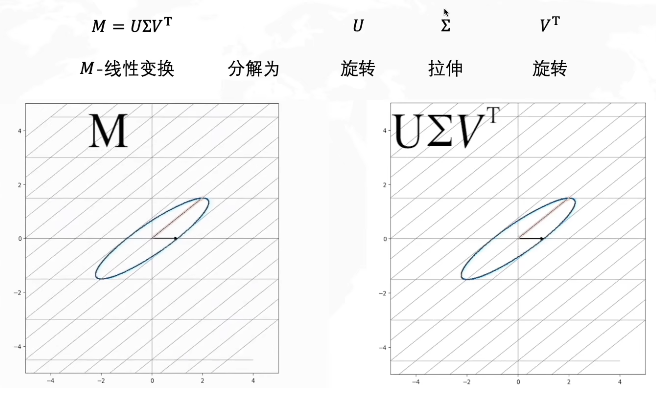
左图中的M是一个线性变换矩阵，想要从一个单位圆达到M这个效果，你可以想象一下，我们就是把这个圆拉长并且旋转。我们可以把整个操作分解为拉伸+旋转。在奇异值分解中，则是分解为了旋转VTV^TVT+拉伸Σ\SigmaΣ+旋转UUU，奇异值分解的公式则是M=UΣVTM=U\Sigma V^TM=UΣVT。

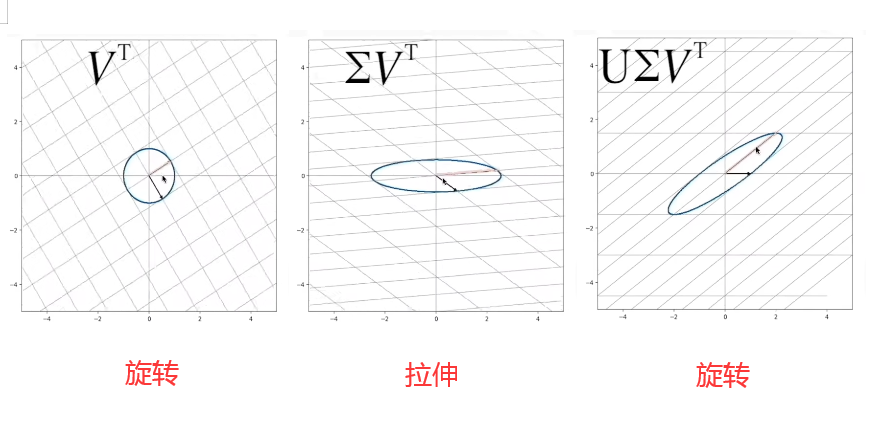
公式推导

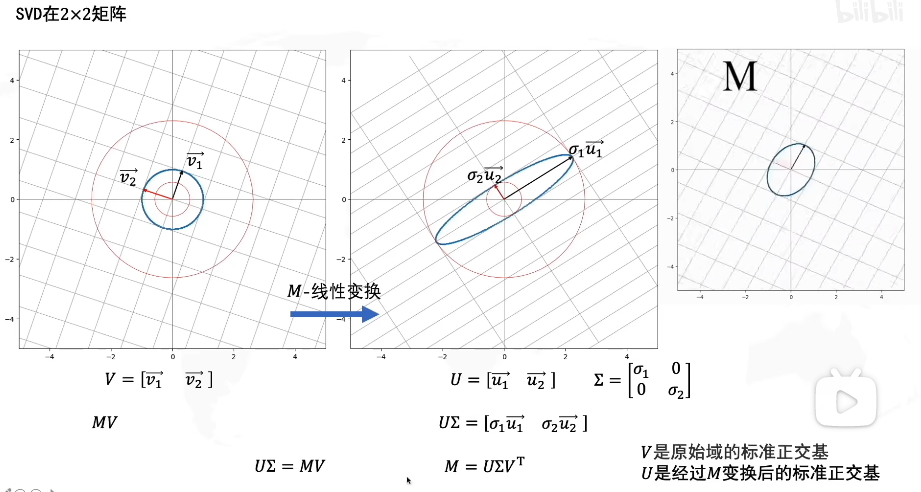
如图，V是原始域的标准正交基（即基为单位长度且正交），我们对其应用线性变换M得到了新的矩阵UΣU\SigmaUΣ，U=[u1→,u2→]U=[\overrightarrow{u_1},\overrightarrow{u_2}]U=[u1​​,u2​​]也是标准正交基（其基为原始域单位长度且正交)，但是我们发现经过线性变换M的新矩阵U，它的基的长度实际上已经不是单位长度了（原始域的单位长度）,相当于在U的基上进行了拉伸，我们用Σ\SigmaΣ表示这个拉伸矩阵，拉伸幅度用奇异值σ\sigmaσ表示。

因此我们可以得到MV=UΣMV=U\SigmaMV=UΣ,其中由于V是正交矩阵，因此VT=V−1V^T=V^{-1}VT=V−1
M=UΣV−1=UΣVTM=U\Sigma V^{-1}=U\Sigma V^TM=UΣV−1=UΣVT

SVD推广到任意大小矩阵

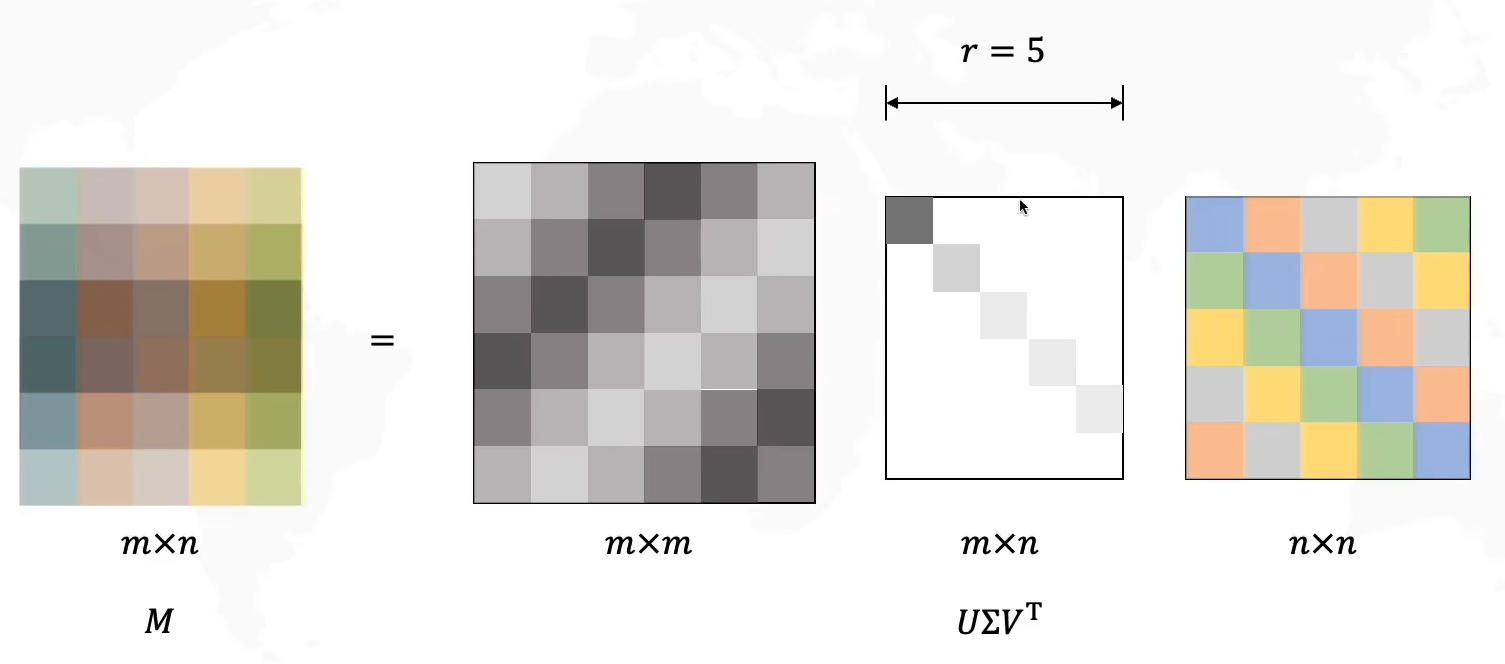
对于任意大小矩阵可化为m×n=(m×m)(m×n)(n×n)

在上图中举出的这个例子中，我们发现Σ\SigmaΣ矩阵中的最后一行是没有信息的，因此这一行可以忽略（在此例子中m=n+1），我们可以少计算一行，将其看作一个(m-1)*n的矩阵，那么UUU矩阵的最后一列也可以消去，因此可以得到一个更简单矩阵计算：

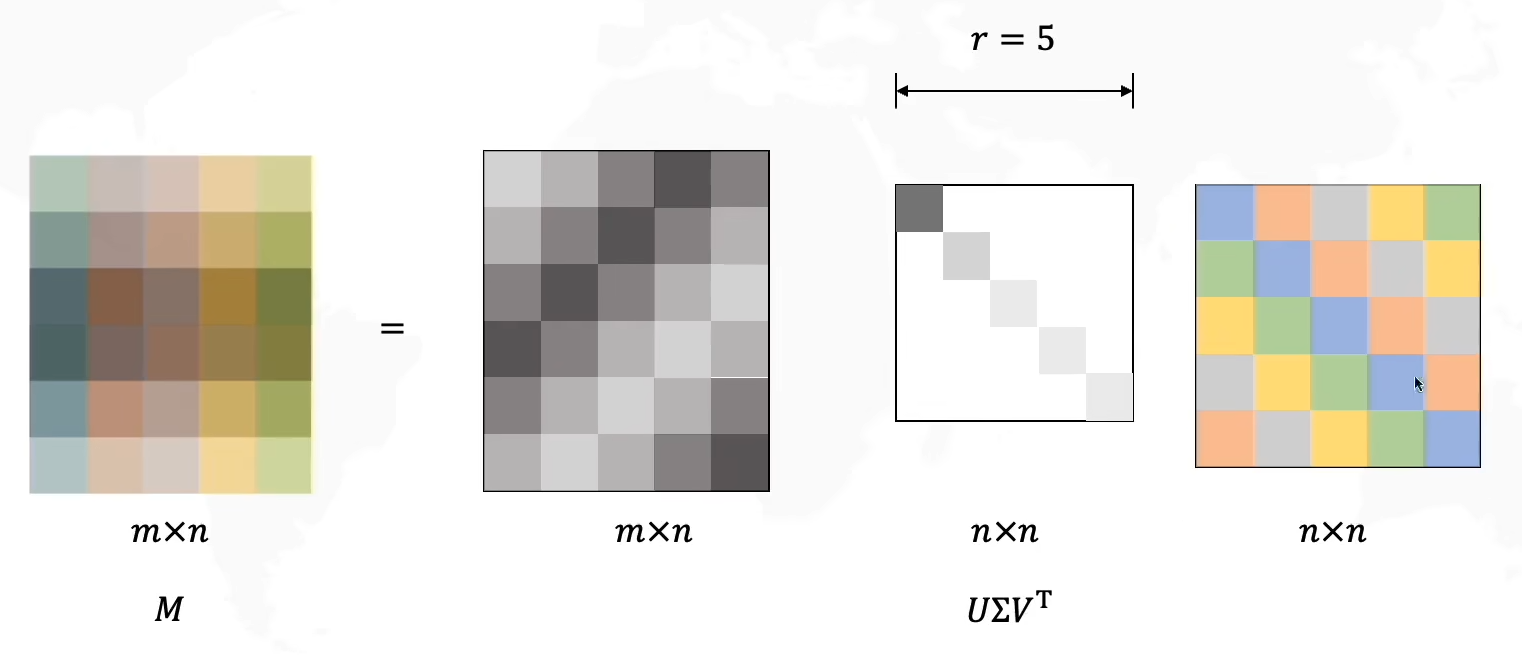
在这里我们稍微提一下后面要讲的主成分分析：其实就是选择主要元素，丢弃非主要元素从而实现信息压缩。
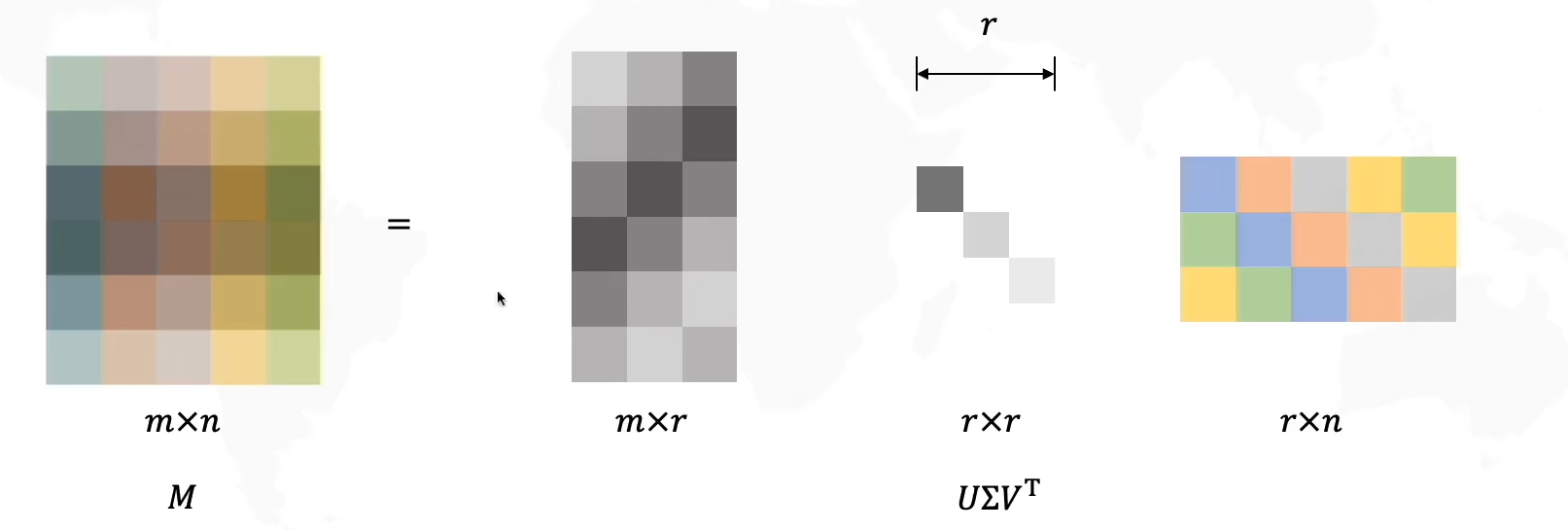现在让我们给Σ\SigmaΣ选择r个主成分，得到新的压缩过的三个矩阵

我们按照Σ\SigmaΣ中奇异值的个数进行模式拆分，由于压缩矩阵是(m×r)(r×r)(r×n),所以我们分别把UUU拆成rrr列，Σ\SigmaΣ拆成rrr个奇异值，VTV^TVT拆成rrr行，依次组合成三个模式(pattern)

将U,VTU,V^TU,VT拆出的成分相乘，得到一个新的矩阵，再分别乘以奇异值，最后将三个矩阵叠加在一起，就得到了原始矩阵M（由于选择了主成分，因此存在信息丢失）

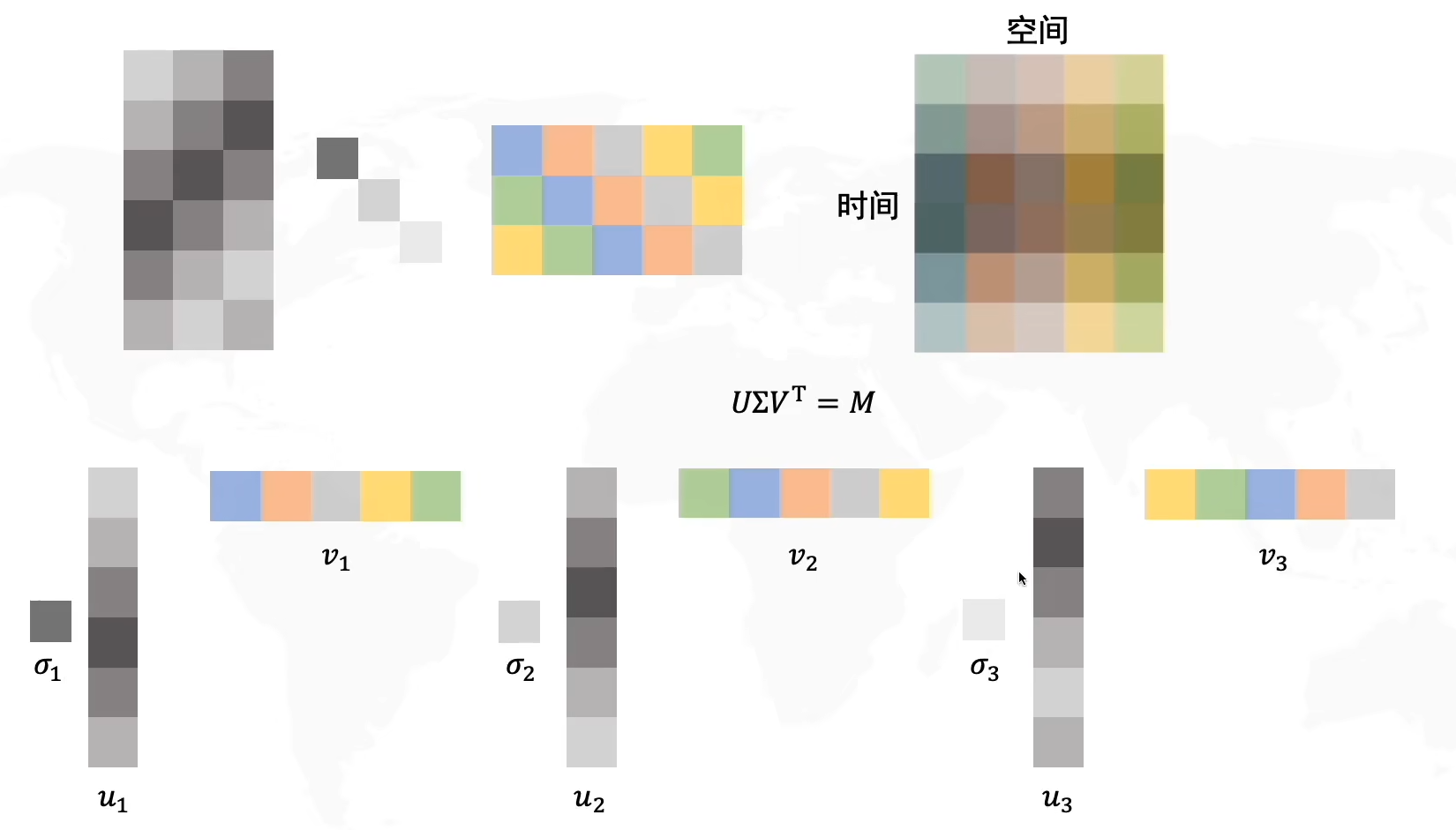
我们再将其拆解出来，就是基向量u∗基向量v∗奇异值σ基向量u*基向量v*奇异值\sigma基向量u∗基向量v∗奇异值σ,因为奇异值有三个，所以我们拆分出了三种模式，我们可以给不同的模式定义不同的信息

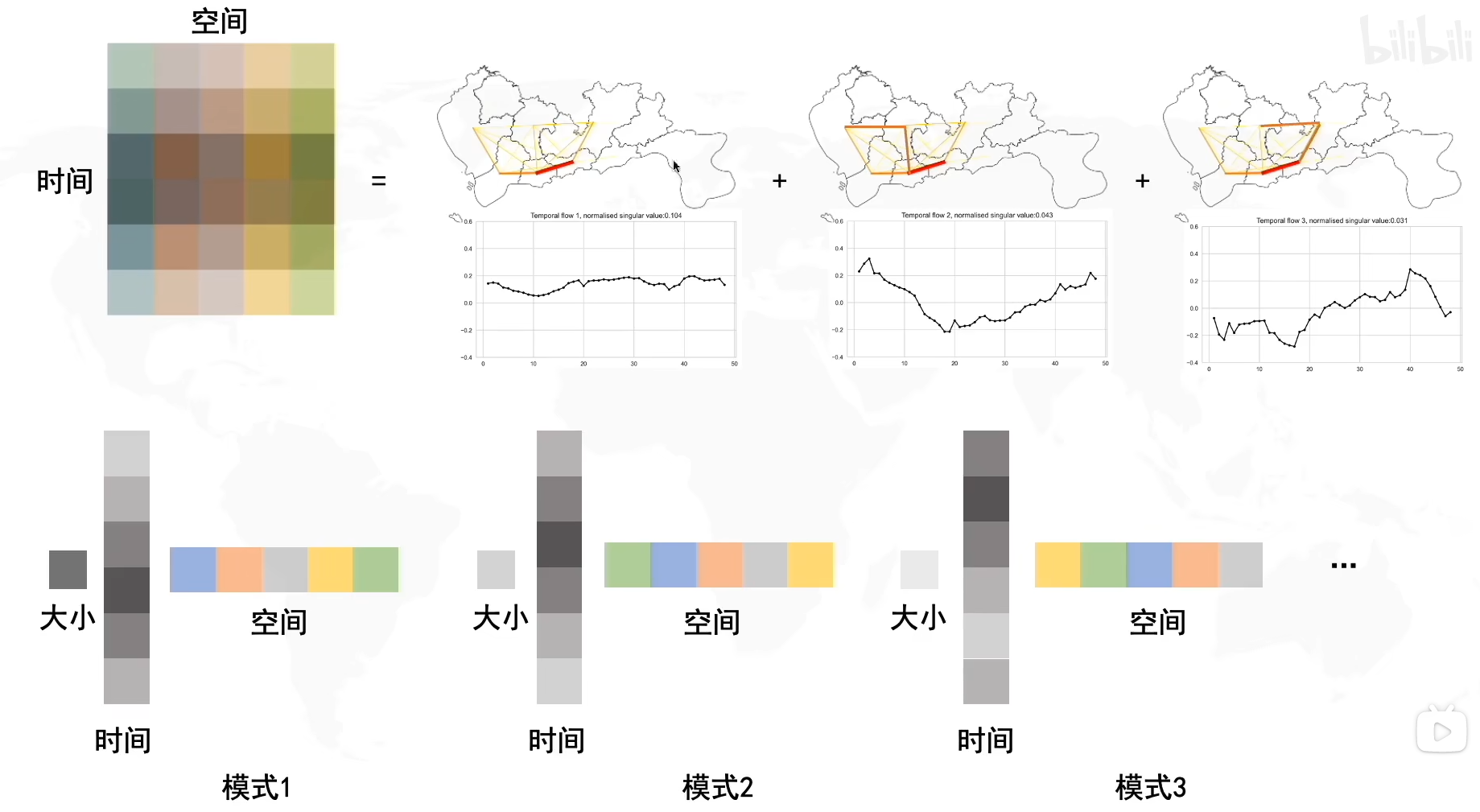
虽然三种模式的保存的信息形式都是时间，空间和大小，但是三种模式保存的时间，空间的分布都是不同的。

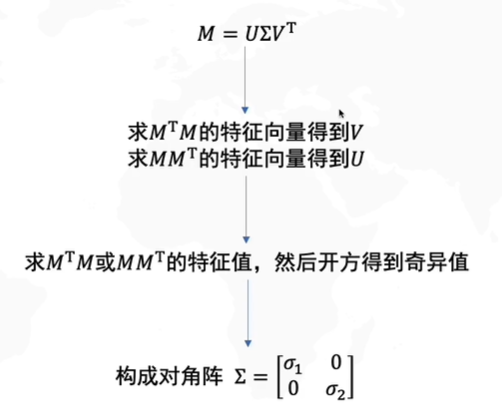
如何求SVD分解

M=UΣVTMTM=(UΣVT)TUΣVTMTM=VΣUTUΣVT(Σ对称)MTM=VΣΣVTM=U\Sigma V^T\\ M^TM=(U\Sigma V^T)^TU\Sigma V^T\\ M^TM=V\Sigma U^TU\Sigma V^T(\Sigma对称)\\ M^TM=V\Sigma\Sigma V^TM=UΣVTMTM=(UΣVT)TUΣVTMTM=VΣUTUΣVT(Σ对称)MTM=VΣΣVT

我们令L=ΣΣL=\Sigma\SigmaL=ΣΣ，我们设MTMM^TMMTM的特征值为λ\lambdaλ,那么就有MTMv→=λv→M^TM\overrightarrow{v}=\lambda\overrightarrow{v}MTMv=λv

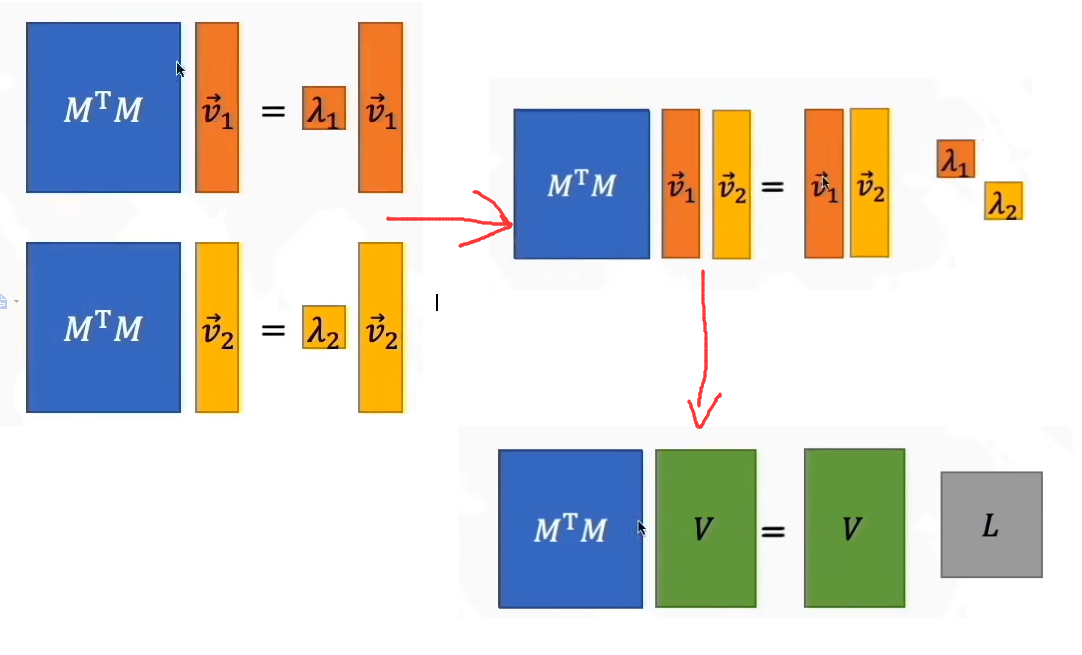
将上式子乘以V−1V^{-1}V−1，我们得到

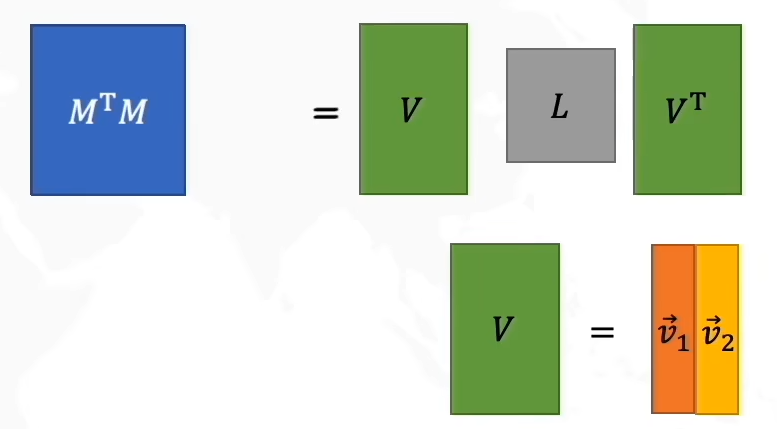
因此我们得到:
MTM=VLVTMTMV=VL=LVMMTU=UL=LU(V和U都是向量,所以能交换位置)M^TM=VLV^T\\ M^TMV=VL=LV\\ MM^TU=UL=LU(V和U都是向量,所以能交换位置)MTM=VLVTMTMV=VL=LVMMTU=UL=LU(V和U都是向量,所以能交换位置)
所以V是MTMM^TMMTM的特征向量,U是MMTMM^TMMT的特征向量，因此Σ\SigmaΣ是矩阵MTM和MMTM^TM和MM^TMTM和MMT的特征值L=Σ2L=\Sigma^2L=Σ2开方构成的对角阵，因此只需知道M，我们就可以进行SVD分解

非负矩阵分解（NMF)

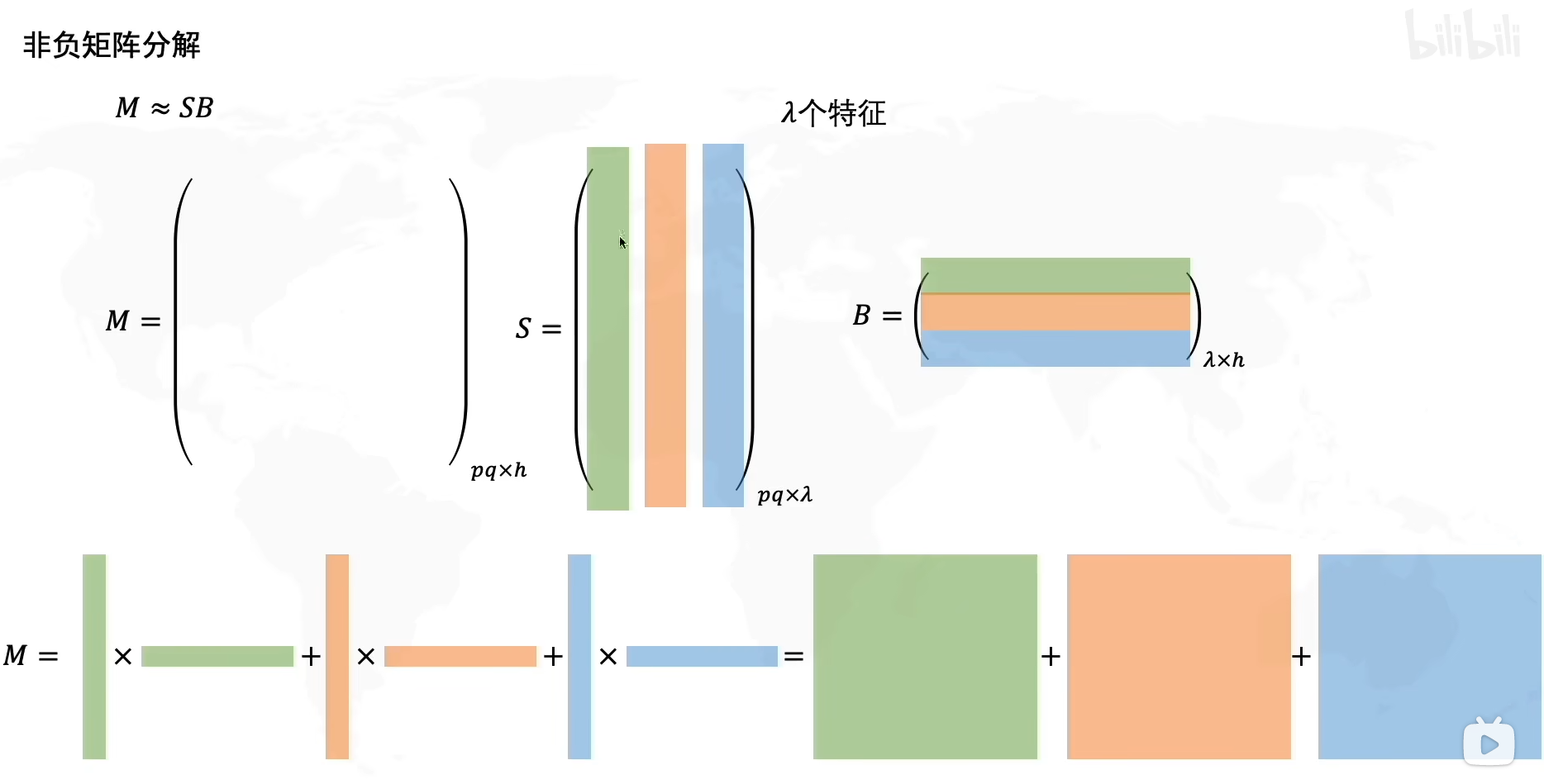视频中只简单的提了一嘴，简单来说非负矩阵分解类似于SVD，将MMM分解为SBSBSB，这两个矩阵中的每个向量，每个元素都是非负的，然后将S的每一列*B的每一行，得到右下角三个秩为1的矩阵并相加，最终结果近似于原始矩阵M，假设S列代表空间，B行代表时间，当时间空间为正值的时候我们比较方便讨论其物理意义。由于缺失了奇异值σ\sigmaσ，所以我们不太好判断哪种模式主要，所以可能我们需要求出矩阵范数来判断每种模式的大小。

主成分分析PCA

我们为什么需要PCA？

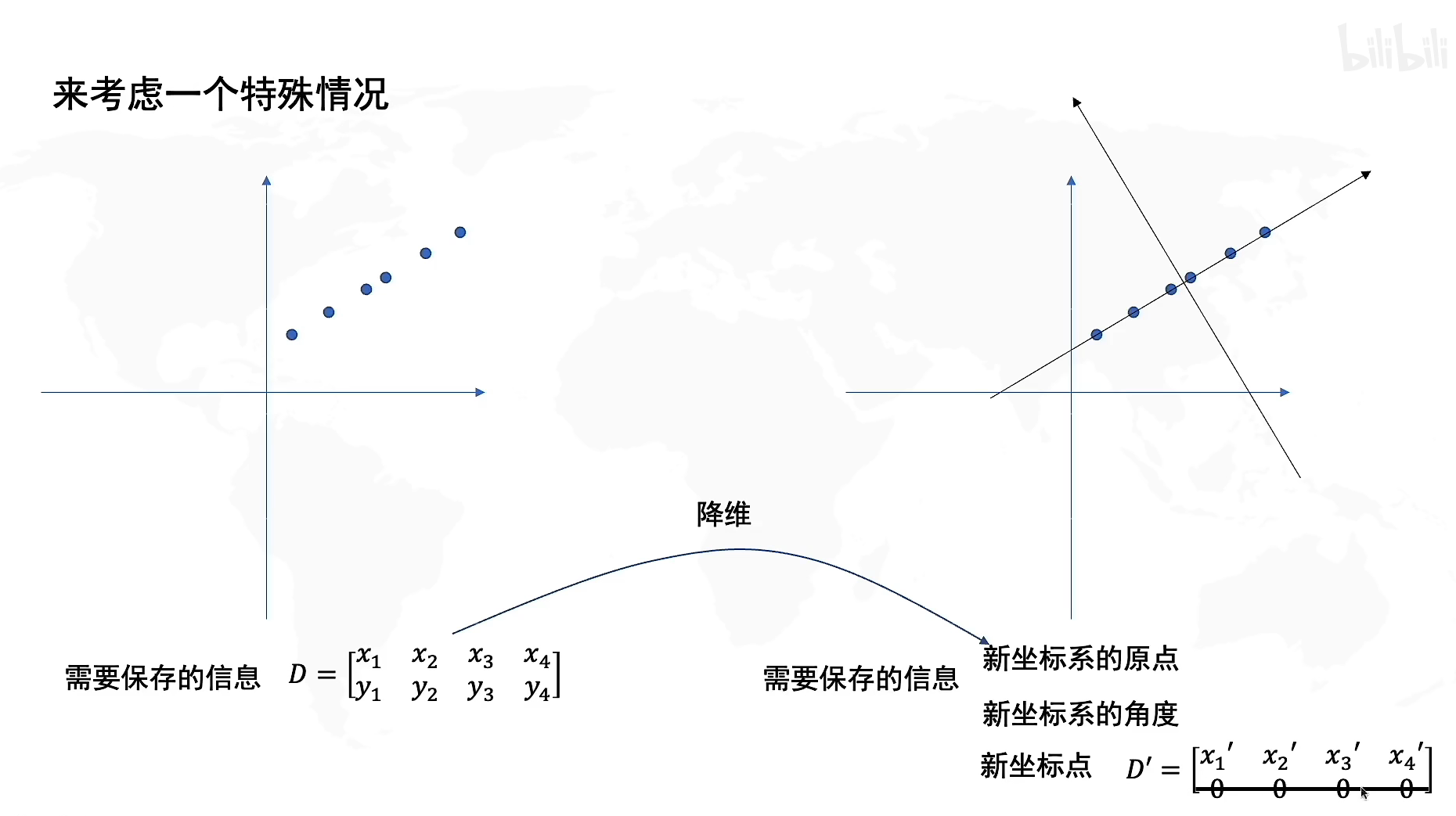
我们来看看一个特殊的例子，如果在二维坐标上保存了这些样本，我们发现实际上它们几乎处于同一条直线，现在我们建立一个新的坐标系，那么如果以新坐标系为原点，就会发现所有的样本基本分布在一维数轴上，也就是说，如果我们使用新的坐标系来保存样本数据，那么我们只需要一维的矩阵就能保存所有信息，这样我们就实现了数据的降维，并且保证了较少的信息损失。

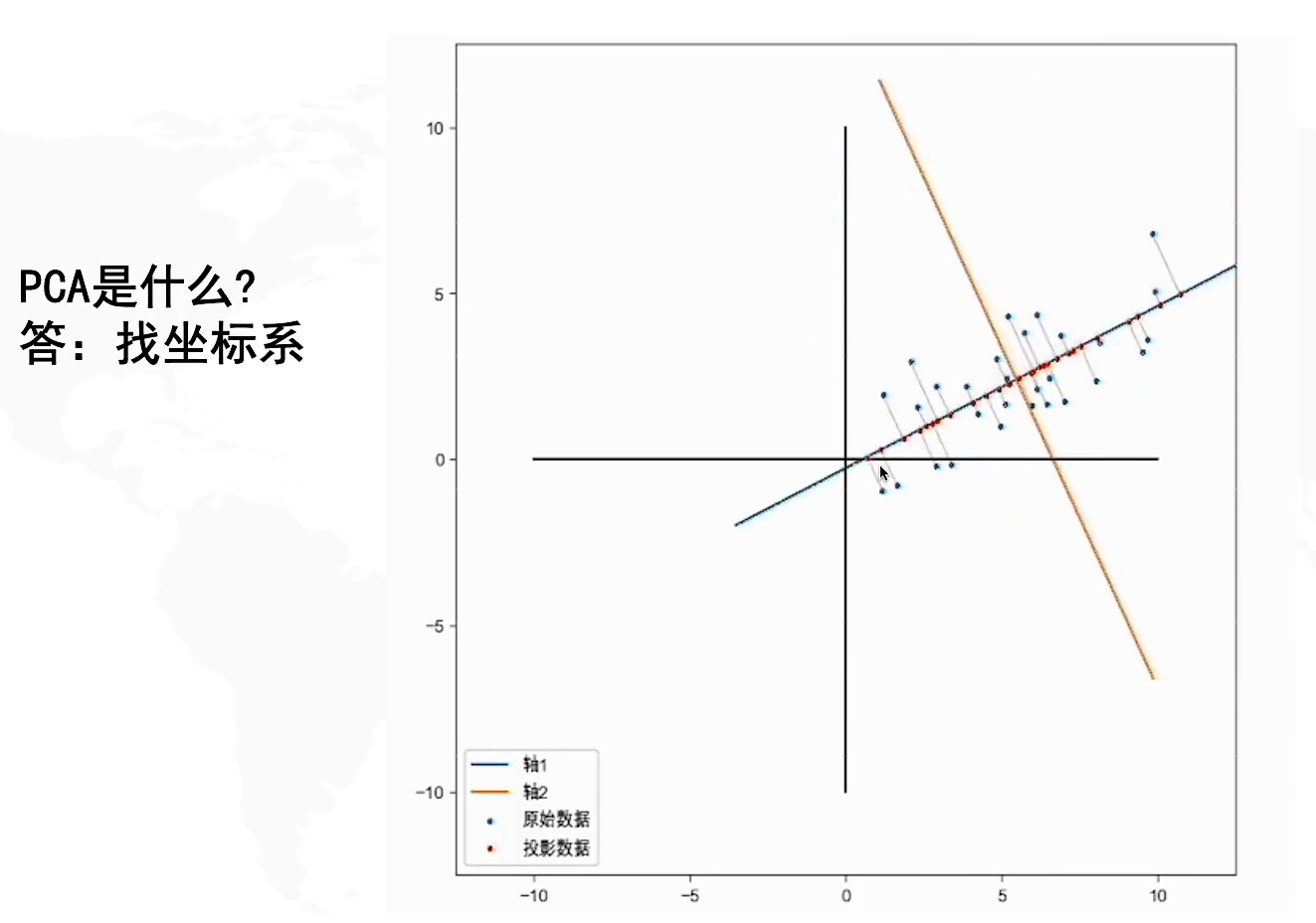
因此，PCA的本质就是重构一个新的坐标系，使得我们在进行数据降维的时候，尽可能多地保存信息，使得信息损失较少。

来找坐标原点

让我们来看一个例子：

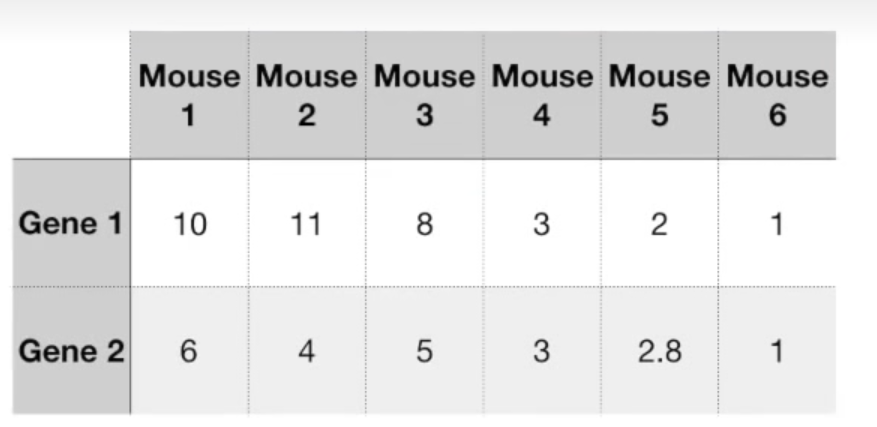
假设我们有6只小鼠，每只测定了两种基因。（其中小鼠意味着个体样本，基因代表每个样本测量的变量）

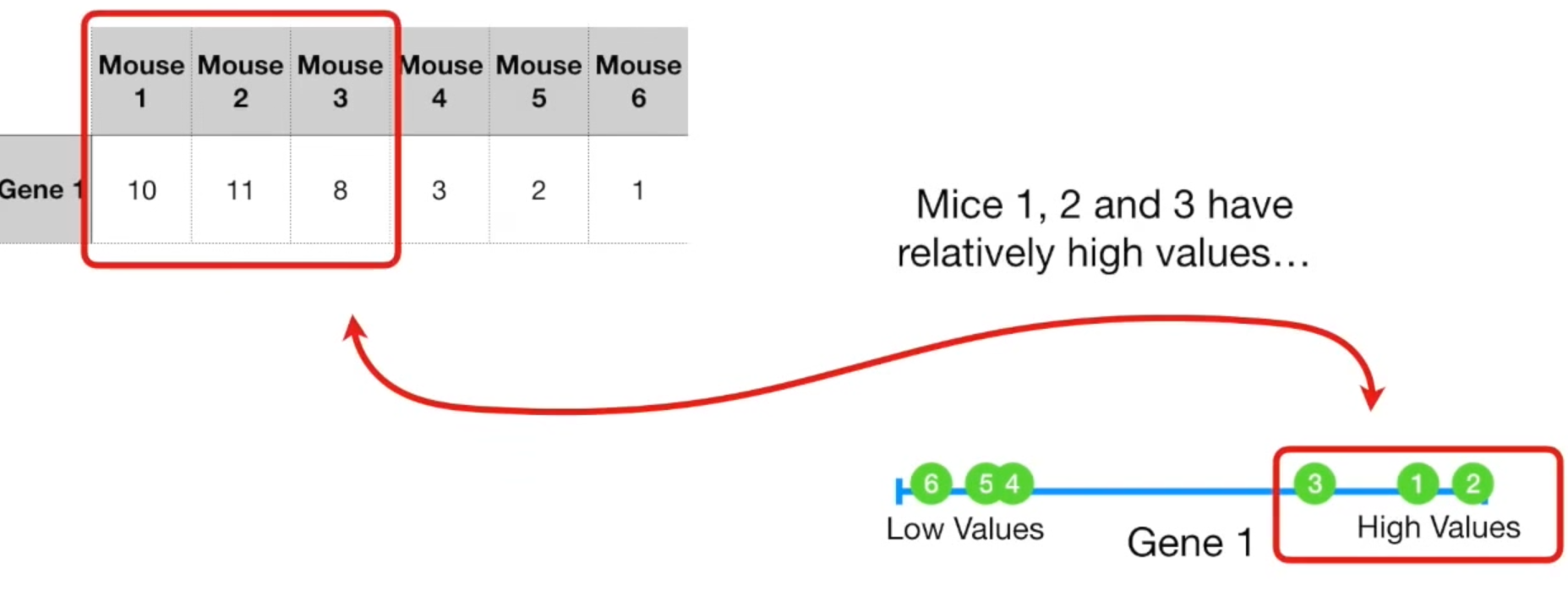假设我们只有一个变量，那么我们可以将数据放在一维数轴上，123处于较高位，456处于较低位，不难发现123是相似的，456是相似的。而这两堆之间的相似性不强。

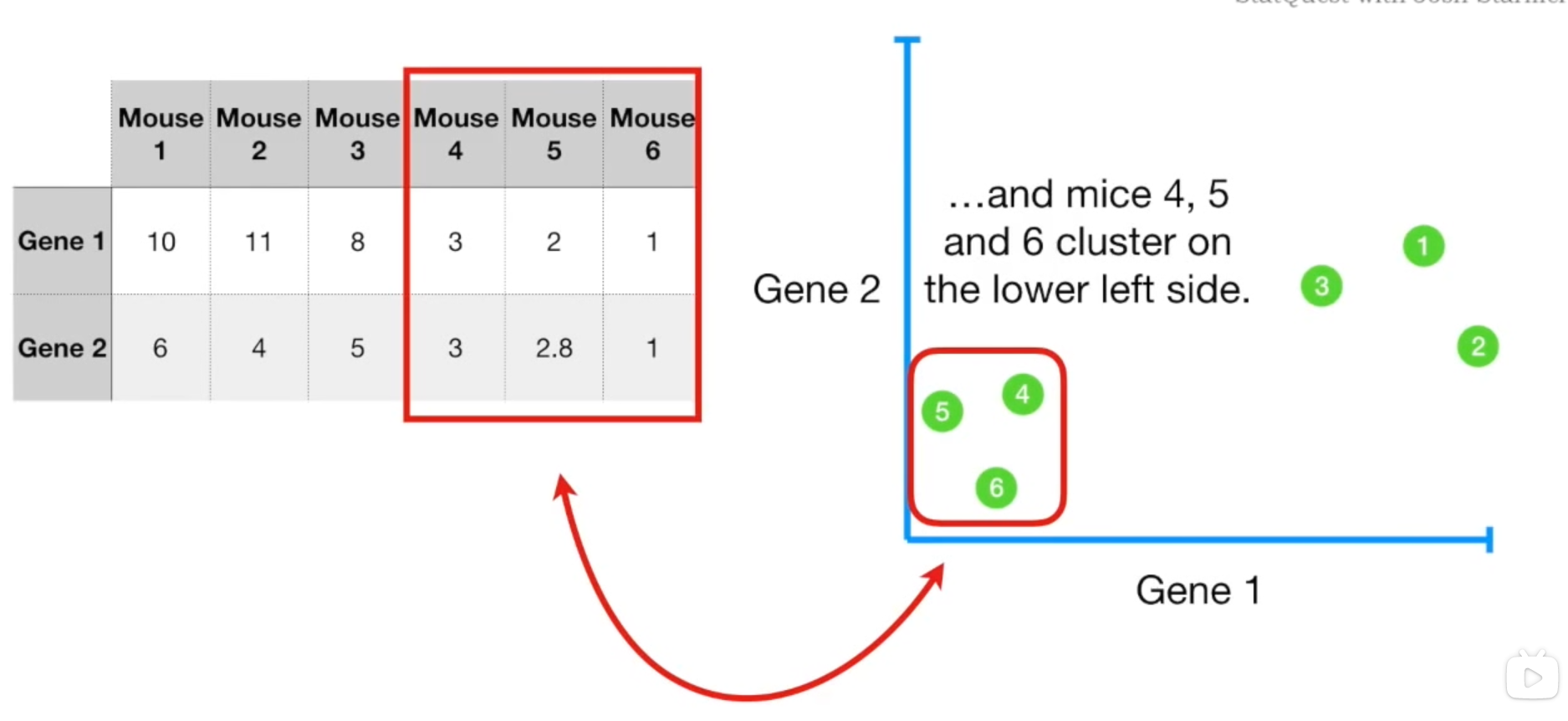
如果有两个变量，拓展到二维坐标上也是同理的。甚至于三维。

但是如果拓展到四维，那我们就没法通过四维图像来判断这些样本的近似度了。

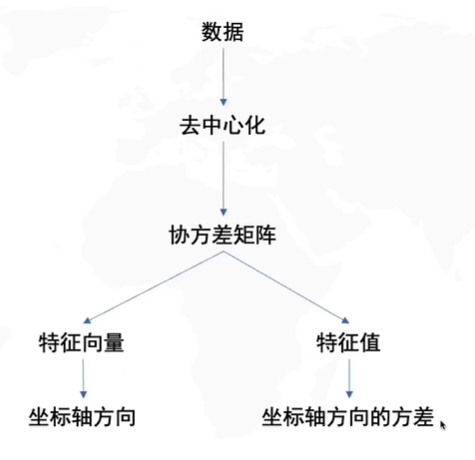
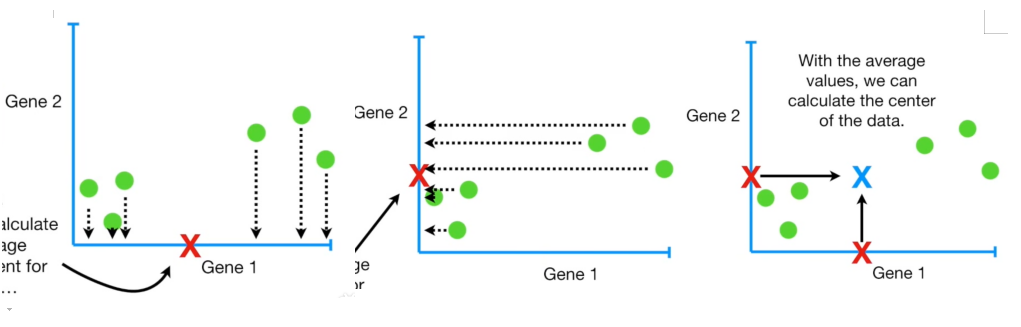如果我们分别计算样本在变量1和变量2上的平均测度（图中红X），我们可以用这个平均值坐标代表数据的中心，我们将这一步称为"去中心化"。确定数据的中心，是为了将其作为坐标原点。

来找坐标系

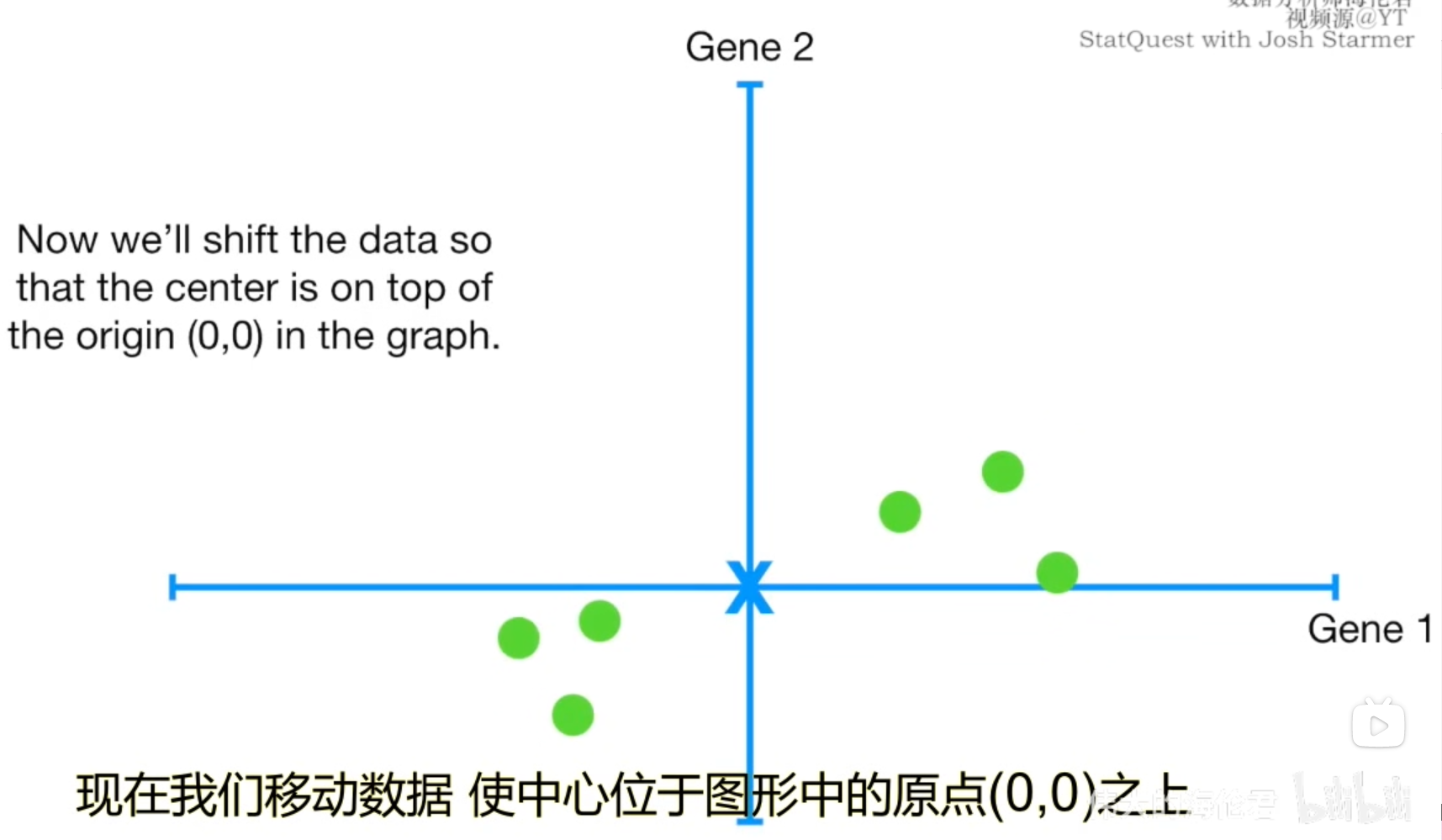现在我们将中心移动到了原点，让我们找到一条直线来拟合这些数据

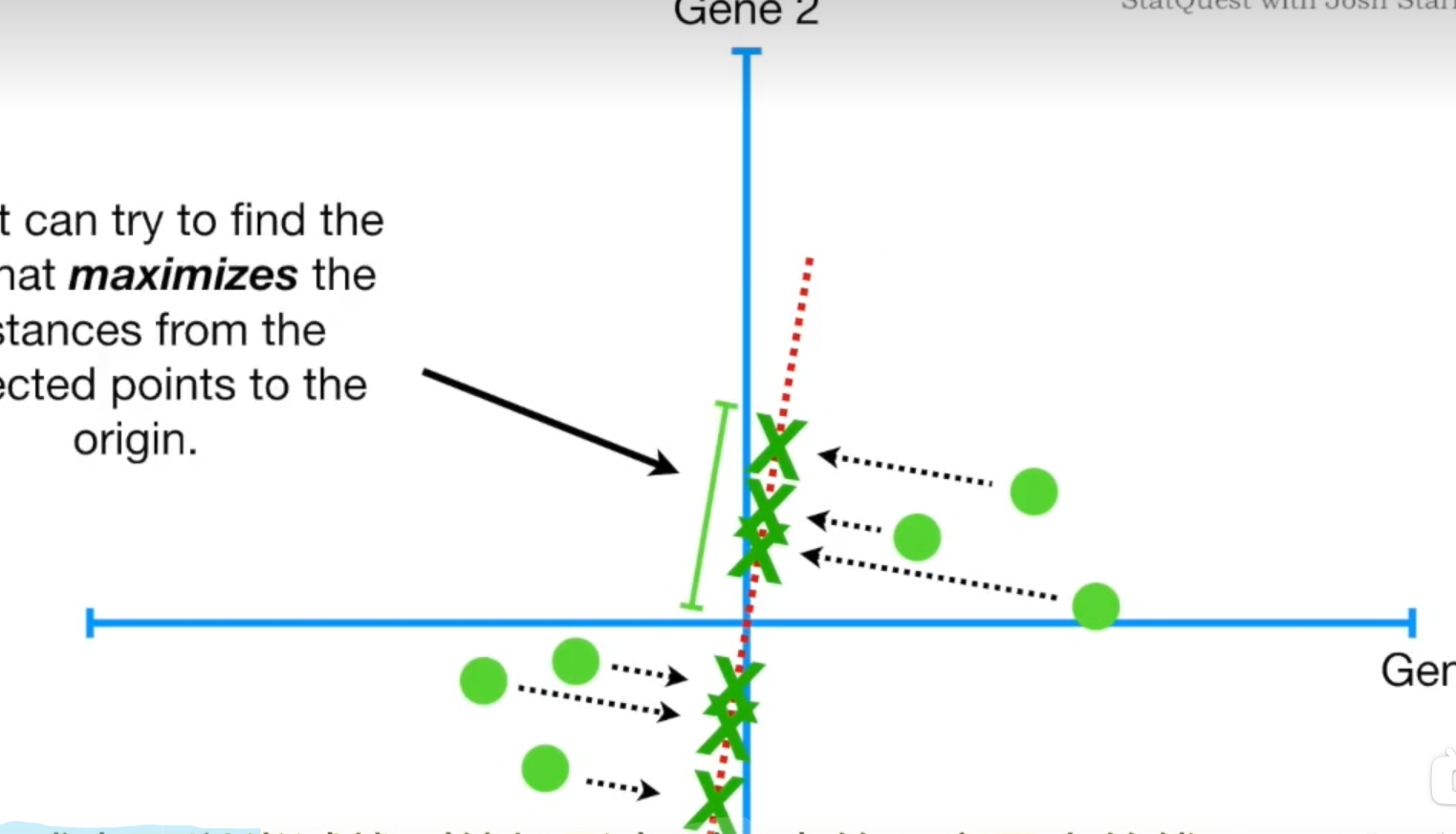怎么寻找最佳拟合直线应该不用我们多说了，最小二乘法。
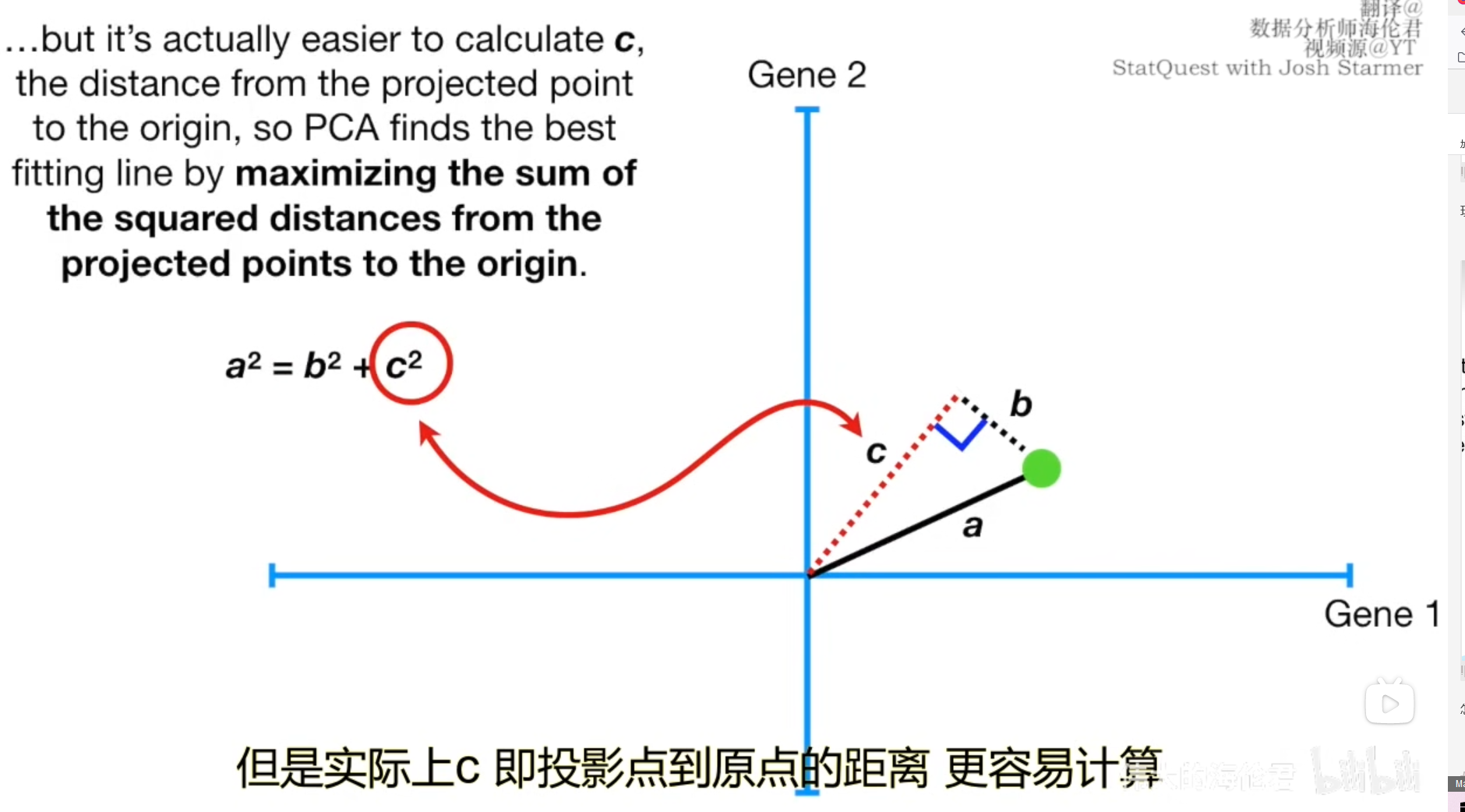现在让我们以一个样本为例，用点到直线的距离和原点构造出三角形，根据勾股定理，a固定，b越短，c越长，b和c是负相关的。也就是说最小二乘法使得所有点到直线的距离bib_ibi​之和最小，如果我们换个角度，那么cic_ici​之和将会达到最大
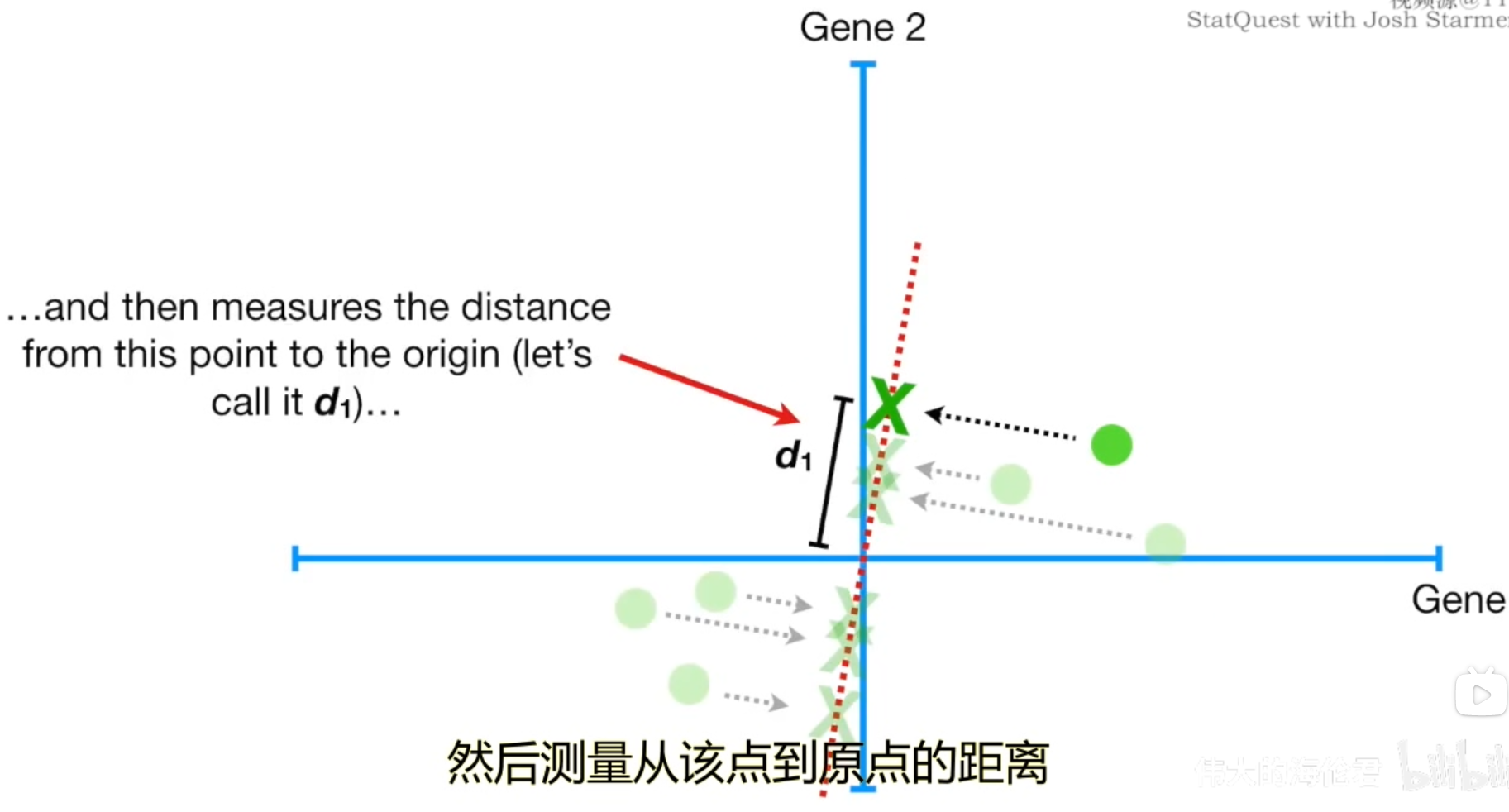因此，我们在PCA中可以通过计算点的投影到原点的距离did_idi​来判断是否找到了最佳拟合直线。需要注意的是，和线性回归不同，由于PCA的坐标存在着正负，因此得到的距离did_idi​也有可能是负数，为了避免负数，因此我们要对其进行平方和计算，其实距离did_idi​意味着方差。

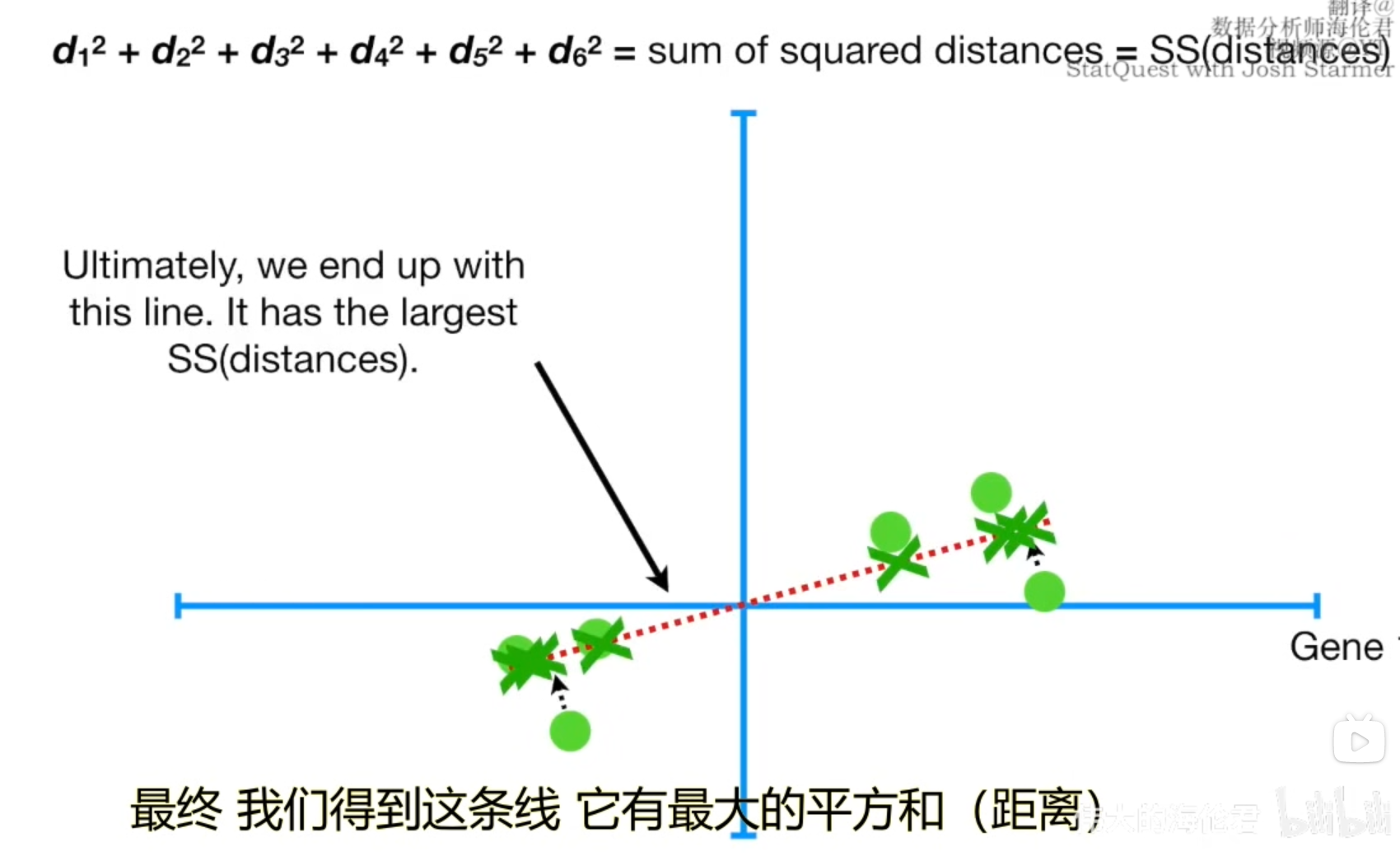
我们将距离平方和称为SS，接下来为了找到这个最佳直线，我们开始旋转，最终找到了这条线，此时的SS是最大的。

我们把现在找到的这条最佳拟合直线称为主成分1(或PC1，Principal Component)，假设它的斜率是0.25,也就是14\frac{1}{4}41​,意味着我们每往横轴前进四个单位，在纵轴上会上升一个单位。

也就是说对于每个数据而言，因为它们的分布是近似于这条直线的，因此每个样本在横轴Gene1的方向上扩散更宽，而在纵轴Gene2的方向上的扩散就相对较小。（就像上图第一象限的样本，它们更偏向右边而不是上面，第三象限的样本更偏向左边而非下面）

我们也可以将PC1这条直线，视为Gene1和Gene2两个变量的线性组合

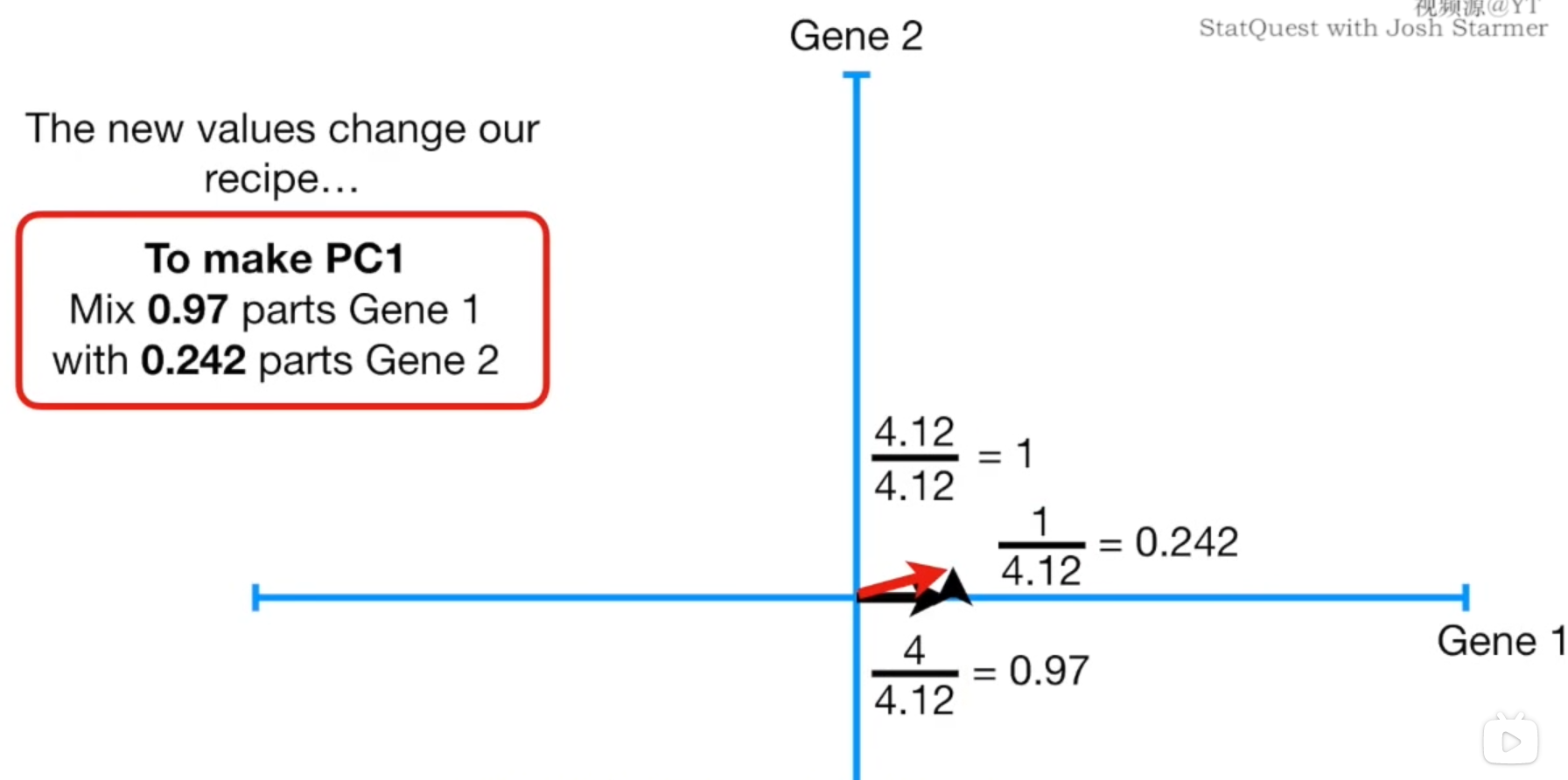
根据勾股定理，我们想要得到单位长度1的PC1，那么我们就需要44.12\frac{4}{4.12}4.124​的Gene1和14.12\frac{1}{4.12}4.121​的Gene2，我们将这个单位长度向量称为PC1的奇异向量或特征向量,我们将每种变量Gene的比例称为载荷得分(Loading Scores)，SS就是PC1的特征值L=ΣΣL=\Sigma\SigmaL=ΣΣ，因此SS\sqrt{SS}SS​就是PC1的奇异值

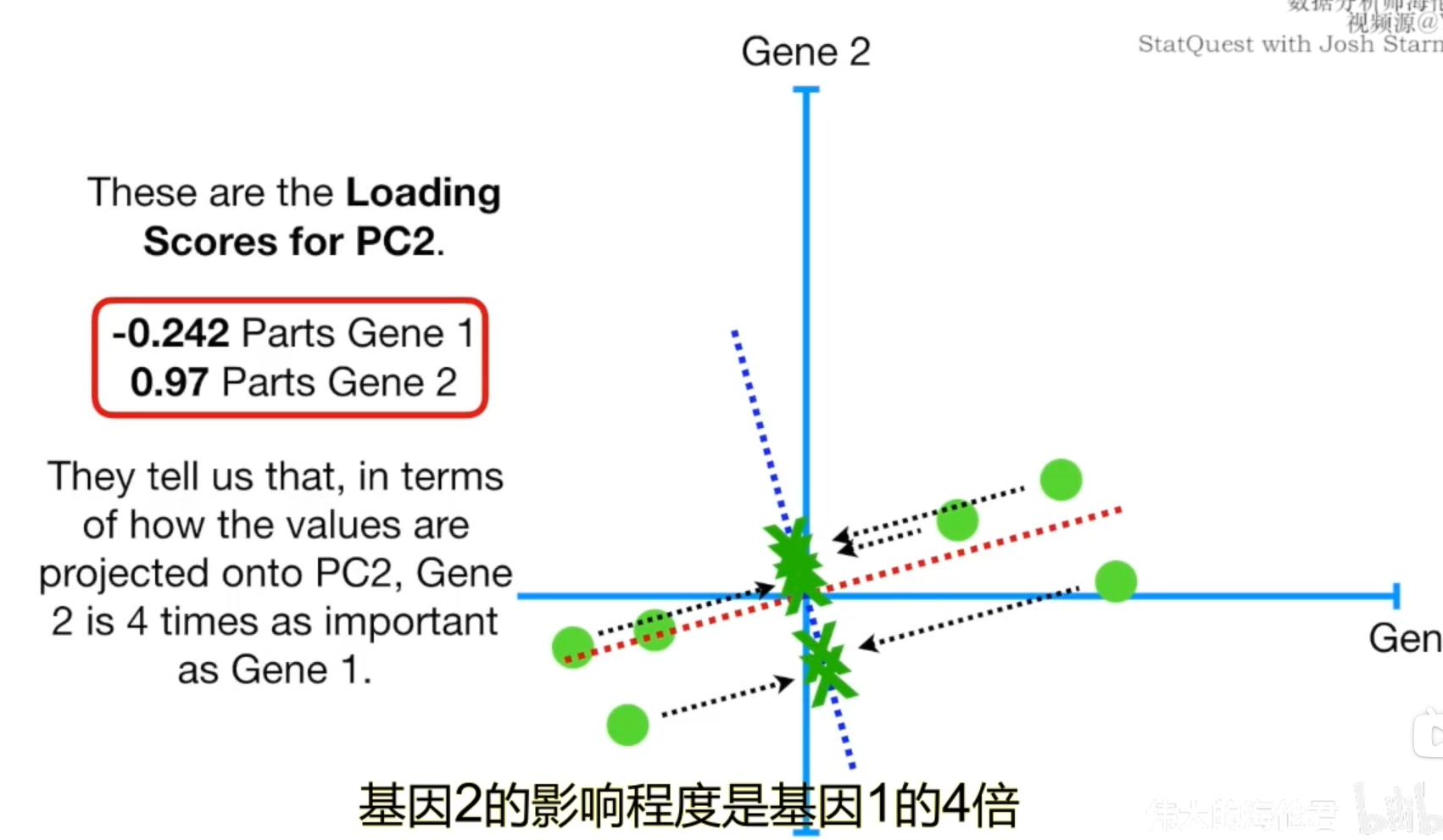
在二维数轴上，PC2就是简单的一条经过原点且垂直于PC1的直线。所以PC2的斜率和PC1的斜率之积是-1，所以当前PC2的斜率为-4。然后我们再求PC2方向上单位长度的特征向量，奇异值以及载荷得分。同时也能得到PC2的SS。

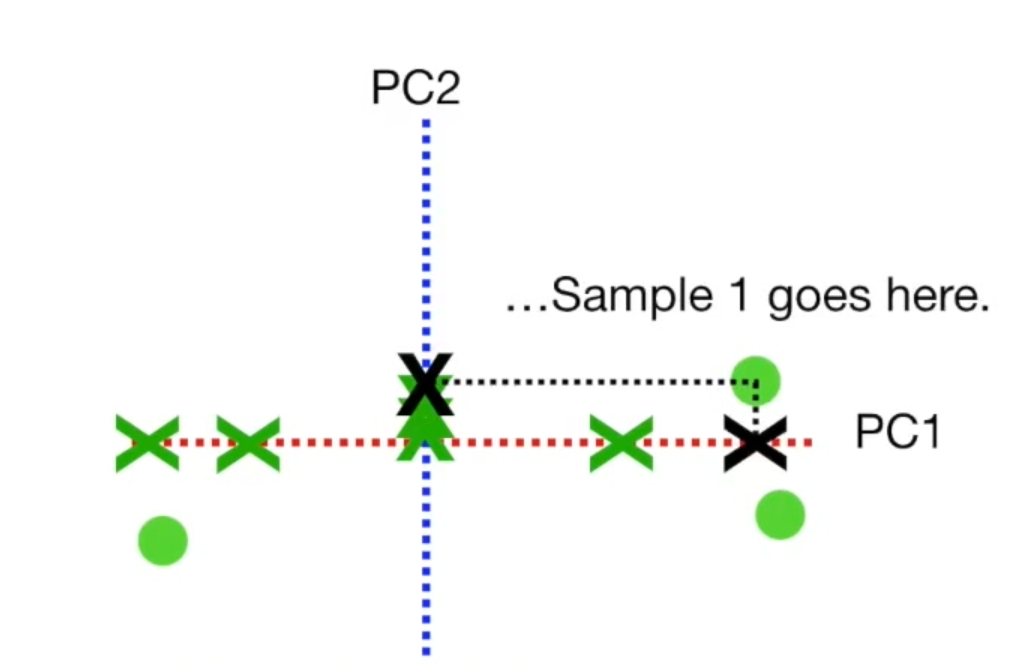
要绘制最终的PCA图，我们需要旋转所有内容，并且使得PC1呈水平状态。然后根据投影位置找到样本，

以上内容是在几何上对PCA的理解，实际上，我们可以将PCA理解为：寻找一个方便我们进行数据降维的特征空间的方法。PC1和PC2都是这个特征空间的轴，而我们之所以要SS（方差）达到最大，是因为方差可以用于解释平行于特征空间轴方向的数据传播

那么我们结合公式推导看看PCA的过程

怎么理解PCA

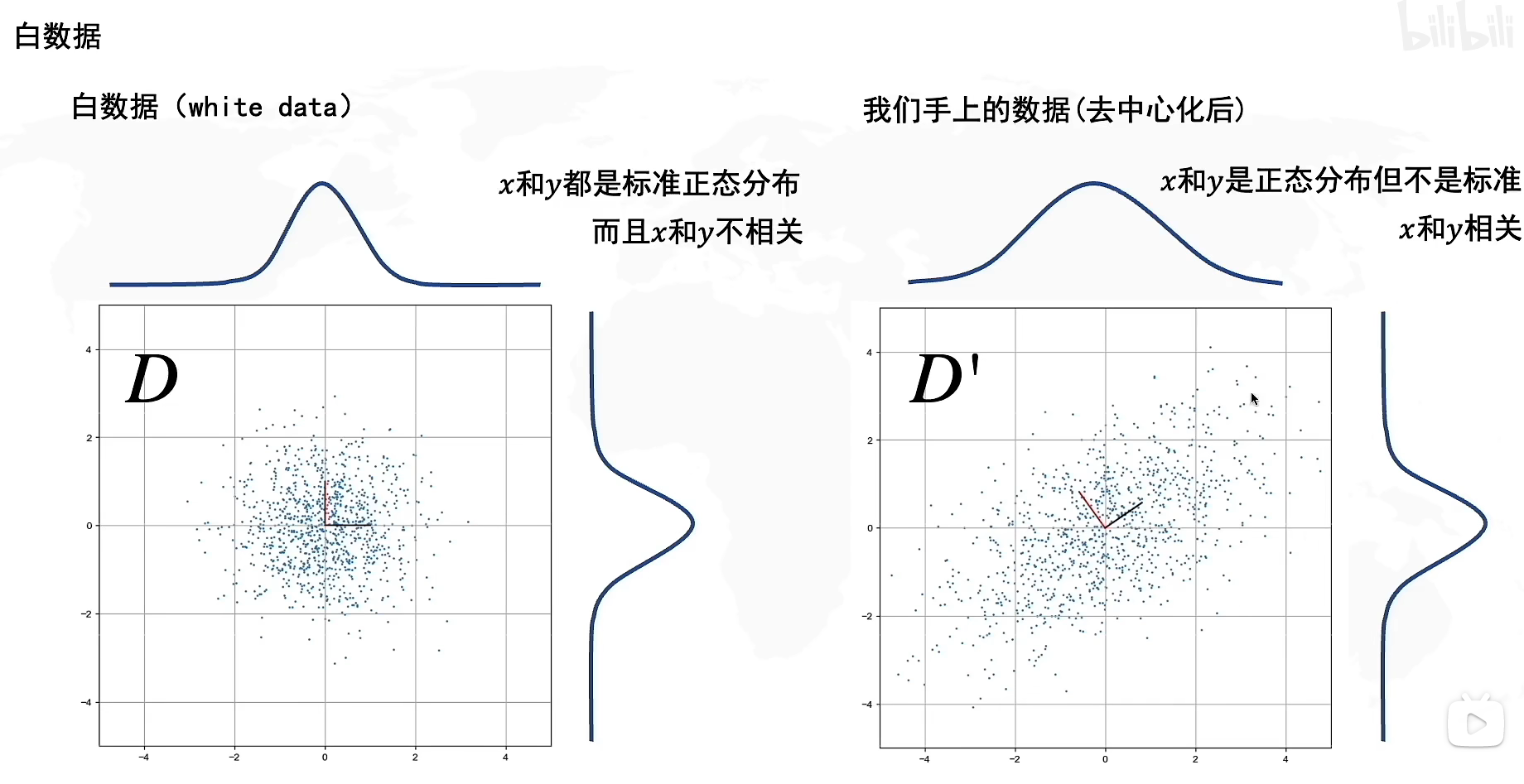
让我们来看看两组数据，第一组数据，它在x，y方向上都是正态分布，并且x和y不相关，我们把第一组数据称为白数据(white data),由于是标准正态分布，因此其均值是0，方差是1。
右边的数据是我们手上去中心化后的数据，x和y都是正态分布但不是标准正态分布，并且x和y相关，意味着随着数据在x方向上的增大，在y方向上也会增大。

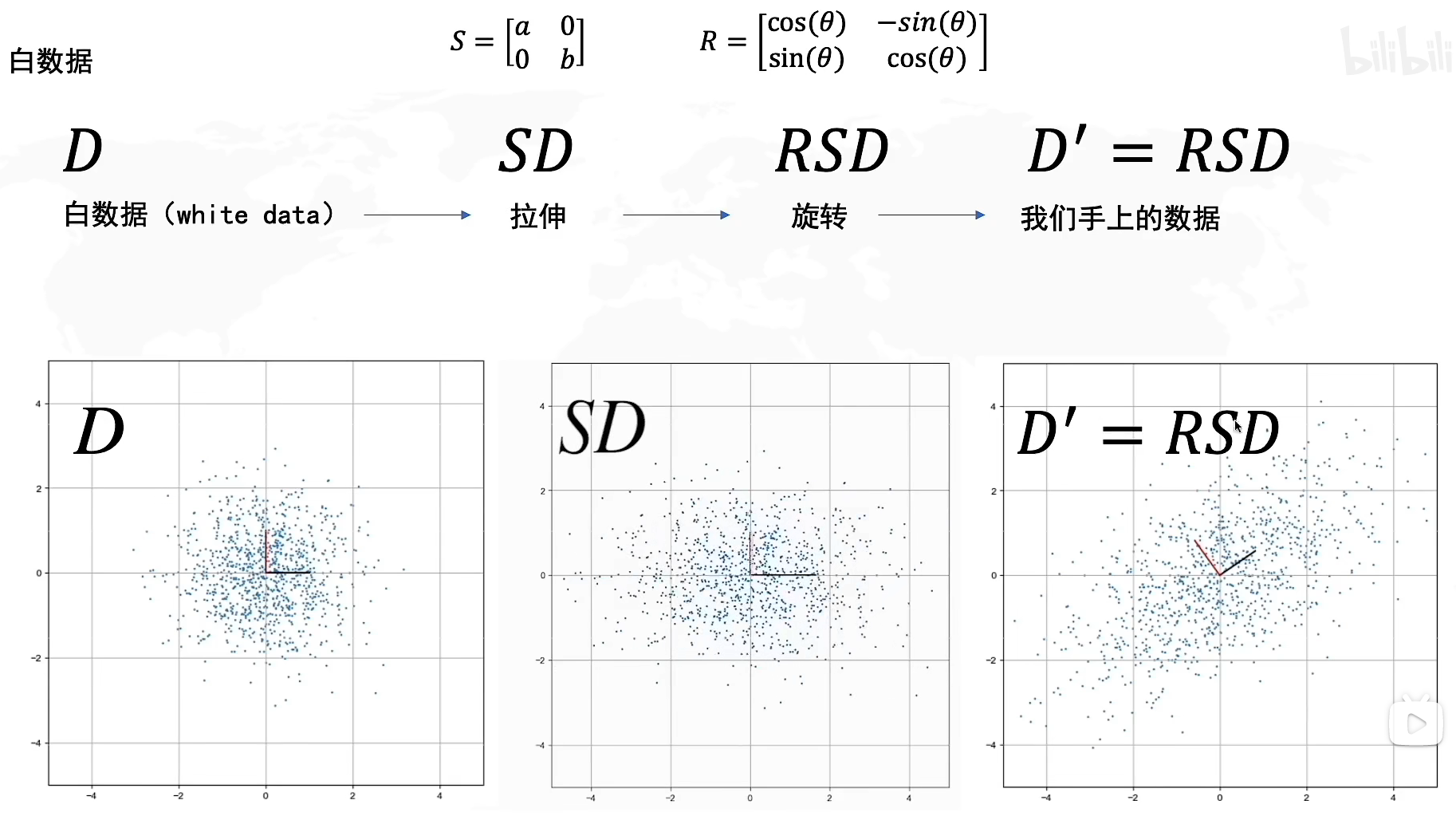
在学习了SVD分解后，我们知道可以通过线性变换将DDD转化为D′D'D′这个矩阵，其中SSS代表我们往方差最大的方向进行拉伸，而RRR则是旋转方向最大的方向的角度，因此我们解决PCA问题可以转化为找到这个旋转矩阵RRR。

同样的，我们也可以通过逆运算，从手上的数据D′D'D′来计算白数据DDD，值得一提的是，由于RRR是一个旋转矩阵，因此基一定是正交的，也就意味着它是一个正交矩阵，因此R−1=RTR^{-1}=R^TR−1=RT,而SSS矩阵是对角矩阵，因此其逆矩阵相当于对角元素的倒数。

什么是协方差矩阵

因此，想要解决PCA问题，我们需要找到旋转矩阵RRR，那么怎么找到它呢？我们需要协方差矩阵的帮助

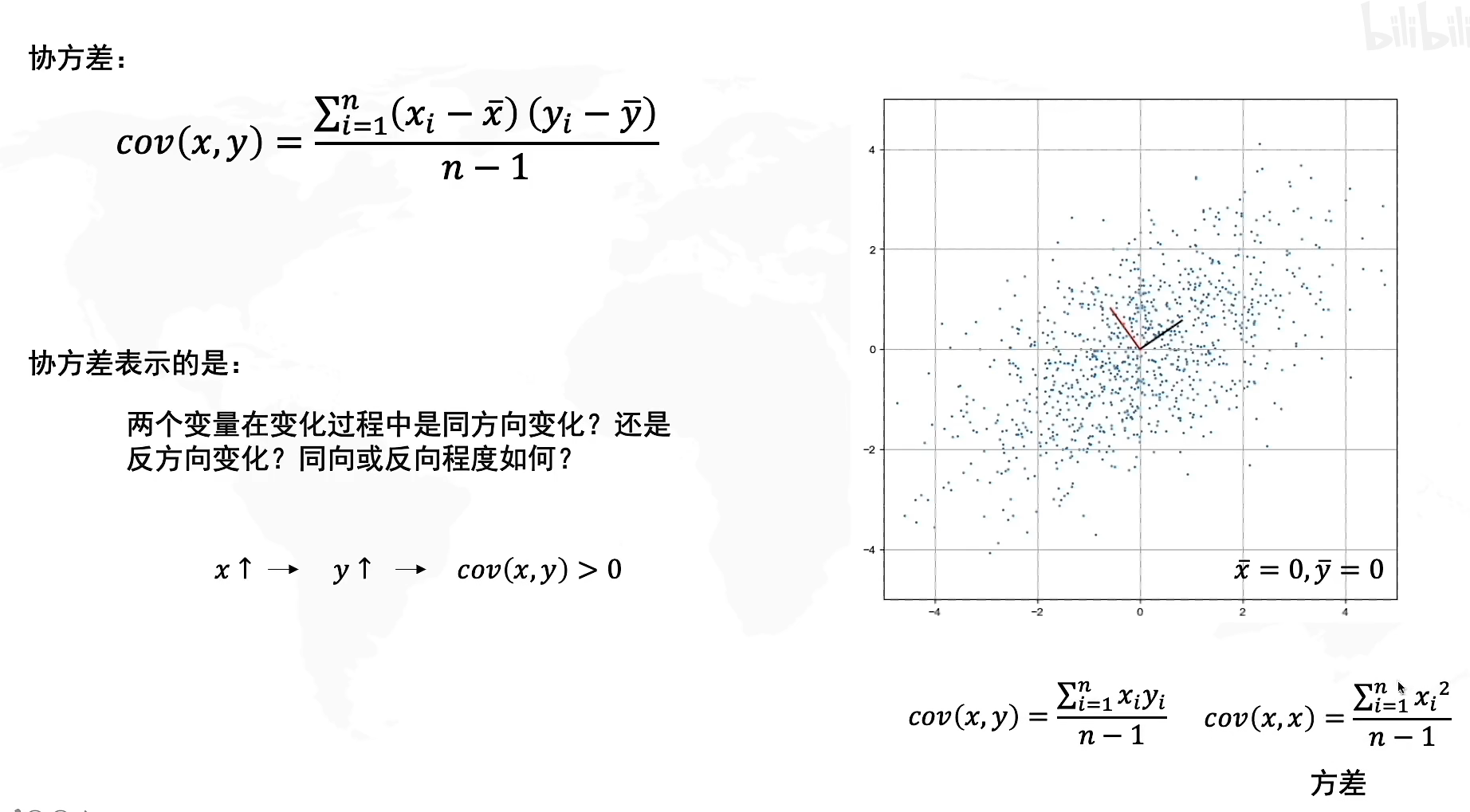
在刚才从几何上理解PCA的过程，我们知道寻找到PC1的条件是要使得方差最大，但是如果运用到计算中，我们的方差公式σ(x)或者σ(y)\sigma(x)或者\sigma(y)σ(x)或者σ(y)只能表示数据在x轴方向上或者y轴方向上的方差，而你可以翻回上面的图看看，我们寻找PC1的时候需要的是对角方向（斜线）上的方差，因此我们需要引入一个新的概念：协方差

协方差，我们用cov(x,y)cov(x,y)cov(x,y)来表示，它代表的是两个变量在变化过程中是同方向变化还是反方向变化？其同向或反向程度如何？它代表了数据在x和y上的相关程度，也就是斜线方向上传播的相关关系。
其中当协方差cov(x,y)>0cov(x,y)>0cov(x,y)>0代表x和y在同方向上相关，反之cov(x,y)<0cov(x,y)<0cov(x,y)<0代表反方向相关，且协方差的绝对值越大代表了方向上的相关程度(变化比例）越大。
协方差公式：cov(x,y)=∑i=1n(xi−x‾)(yi−y‾)n−1cov(x,y)=\frac{\sum^n_{i=1}(x_i-\overline x)(y_i-\overline y)}{n-1}cov(x,y)=n−1∑i=1n​(xi​−x)(yi​−y​)​

其中x‾,y‾\overline x,\overline yx,y​代表了各个样本的x和y在数轴上的均值，由于我们已经完成了去中心化，因此坐标原点处于样本中心，所以x‾=0,y‾=0\overline x=0,\overline y=0x=0,y​=0，因此协方差化简为cov(x,y)=∑i=1n(xi)(yi)n−1cov(x,y)=\frac{\sum^n_{i=1}(x_i)(y_i)}{n-1}cov(x,y)=n−1∑i=1n​(xi​)(yi​)​，如果我们求x与x 的协方差，其结果就是x的方差

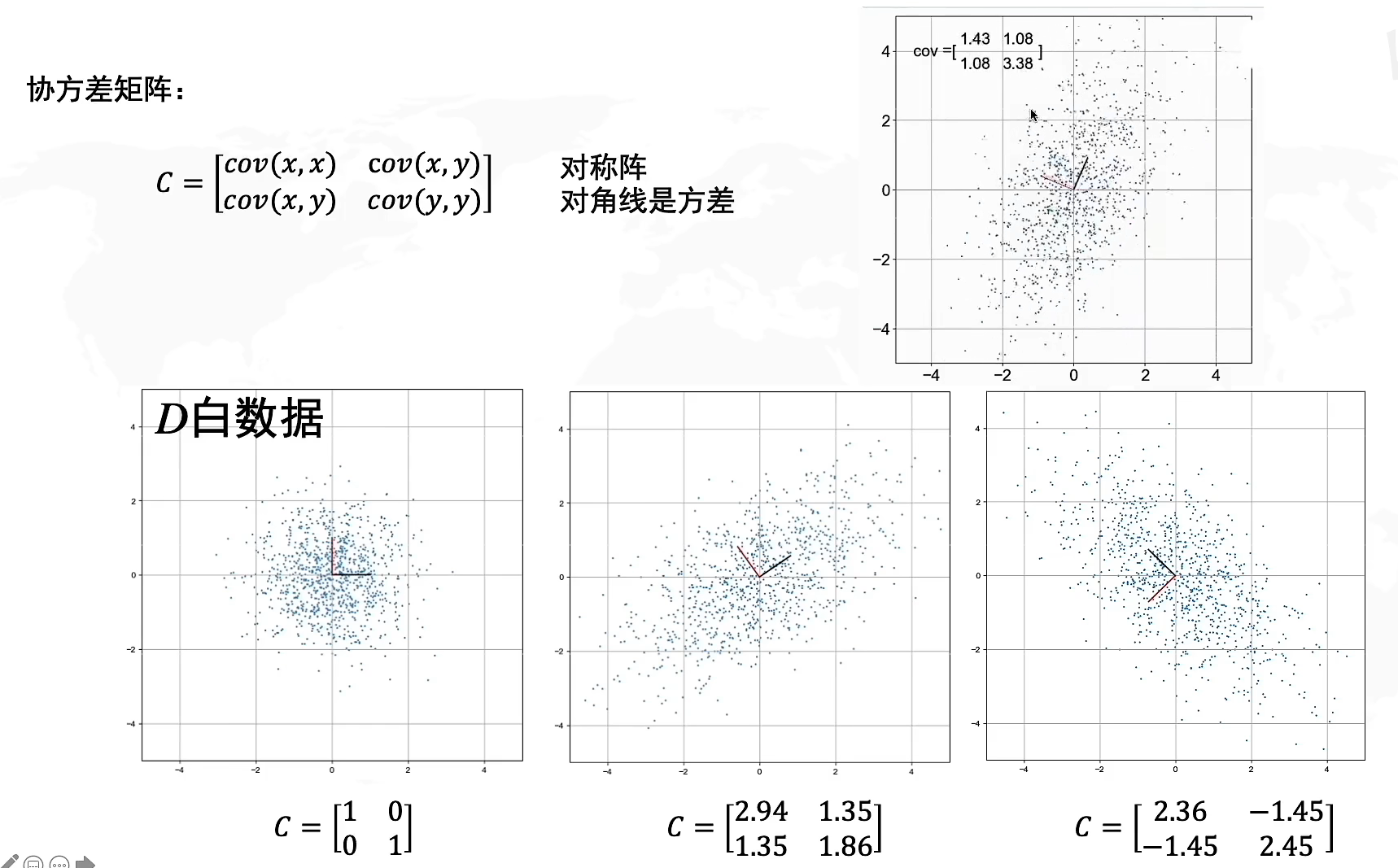
协方差矩阵就是由协方差构成的矩阵，其中对角线元素是方差，n阶矩阵代表了n维坐标。初始的白数据我们说过，由于满足标准正态分布，所以协方差是0，方差是1，因此协方差矩阵C=[1001]C=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}C=[10​01​]

协方差在我们进行矩阵的线性变换的时候是怎么变动的呢？你可以想象一下，由于协方差矩阵C=[cov(x,x)cov(x,y)cov(x,y)cov(y,y)]C=\begin{bmatrix} cov(x,x) & cov(x,y) \\ cov(x,y)& cov(y,y) \end{bmatrix}C=[cov(x,x)cov(x,y)​cov(x,y)cov(y,y)​]，所以当x,y上的向量变动会导致对应的协方差产生变动，因此你可以将其等价为基向量的线性变换所产生的相关性变化。

假设我们将数据向x轴两边拉伸，那么与x相关的协方差cov(x,x),cov(x,y)cov(x,x),cov(x,y)cov(x,x),cov(x,y)会发生变化，而cov(y,y)cov(y,y)cov(y,y)不会，因此想象一下整体数据往x轴两边扩张，y不变，因此x和x，x和y的相关性都会变大，意味着协方差的正负号不变，绝对值增大。反之若是向x轴内收缩，则协方差正负号不变，绝对值缩小。

当数据整体进行旋转的时候，我们以当前xy方向作为对比，想象一下当整体旋转九十度，那么原来的x坐标指向y坐标，而y坐标指向了x坐标的反向，因此方差cov(x,x),cov(y,y)cov(x,x),cov(y,y)cov(x,x),cov(y,y)相关程度不变，协方差cov(x,y)cov(x,y)cov(x,y)符号会产生正负变化，相当于每旋转90度，cov(x,y)∗−1cov(x,y)*-1cov(x,y)∗−1。形状上来看如果形状类似“/”那协方差cov(x,y)>0cov(x,y)>0cov(x,y)>0，反之形状类似""则协方差cov(x,y)<0cov(x,y)<0cov(x,y)<0

详见协方差矩阵的几何解释

公式推导

还是要提一下，上式的矩阵D其实就是SVD里的矩阵M，让我们详解一下协方差矩阵的求法：
C=[cov(x,x)cov(x,y)cov(x,y)cov(y,y)]=[∑i=1nxi2n−1∑i=1nxiyin−1∑i=1nxiyin−1∑i=1nyi2n−1]C=\begin{bmatrix} cov(x,x) & cov(x,y) \\ cov(x,y)& cov(y,y) \end{bmatrix}=\begin{bmatrix} \frac {\sum^n_{i=1}x_i^2}{n-1} & \frac {\sum^n_{i=1}x_iy_i}{n-1} \\ \frac {\sum^n_{i=1}x_iy_i}{n-1}& \frac {\sum^n_{i=1}y_i^2}{n-1} \end{bmatrix}C=[cov(x,x)cov(x,y)​cov(x,y)cov(y,y)​]=[n−1∑i=1n​xi2​​n−1∑i=1n​xi​yi​​​n−1∑i=1n​xi​yi​​n−1∑i=1n​yi2​​​]
这个矩阵相乘结果可以提取1n−1\frac{1}{n-1}n−11​最终化为协方差矩阵C=1n−1DDTC=\frac{1}{n-1}DD^TC=n−11​DDT的矩阵与其转置的乘积形式

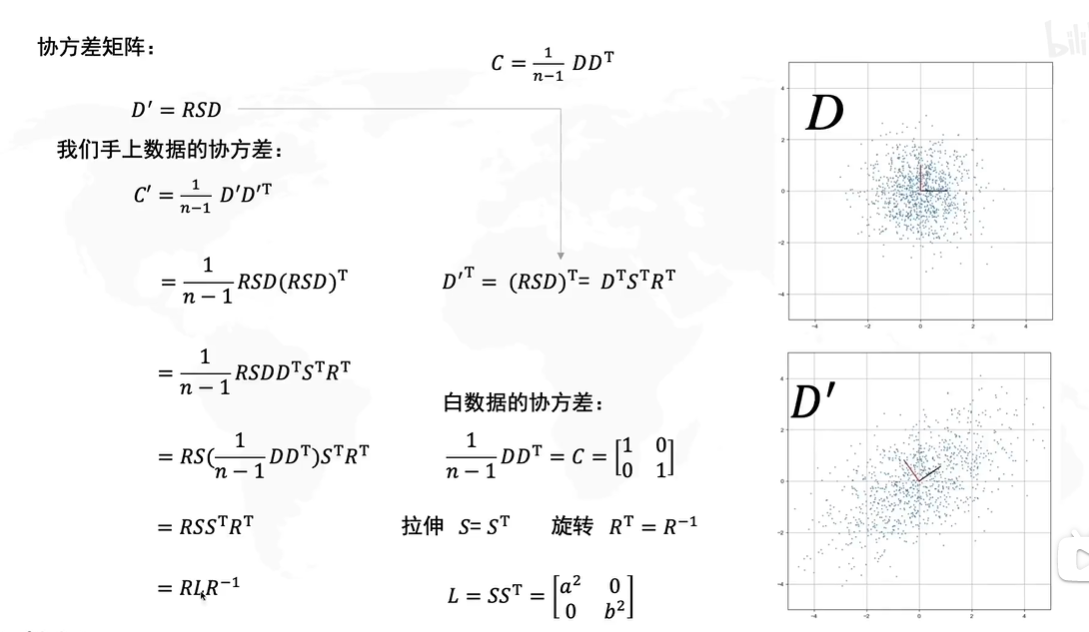
让我们将C′=1n−1D′DTC'=\frac {1}{n-1}D'D^TC′=n−11​D′DT这个式子拆开
=1n−1RSD(RSD)T=1n−1RSDDTSTRT=RS(1n−1DDT)STRT=\frac{1}{n-1}RSD(RSD)^T\\ =\frac{1}{n-1}RSDD^TS^TR^T\\ =RS(\frac{1}{n-1}DD^T)S^TR^T=n−11​RSD(RSD)T=n−11​RSDDTSTRT=RS(n−11​DDT)STRT
因为我们知道白数据的方差是0，协方差是1，所以白数据的协方差矩阵C=1n−1DDT=[1001]C=\frac{1}{n-1}DD^T=\begin{bmatrix} 1 & 0 \\ 0& 1 \end{bmatrix}C=n−11​DDT=[10​01​],因此白数据的协方差矩阵是单位矩阵，所以原式子：
=RSSTRT=RSS^TR^T=RSSTRT
而我们之前说了，拉伸矩阵SSS是一个对角矩阵，所以S=STS=S^TS=ST,旋转矩阵RRR是一个正交矩阵，因此RT=R−1R^T=R^{-1}RT=R−1

原式=RLR−1原式=RLR^{-1}原式=RLR−1

因此我们得出D′D'D′的协方差矩阵 C′=RLR−1C'=RLR^{-1}C′=RLR−1,其中L=SST=[a200b2]L=SS^T=\begin{bmatrix} a^2 & 0 \\ 0& b^2 \end{bmatrix}L=SST=[a20​0b2​]

那么其实到这里我们就已经很熟悉了，这个协方差矩阵和我们在SVD中学到的M=UΣVTM=U\Sigma V^TM=UΣVT的形式已经完全一致了，实际上两者本质上可以说就是同一个式子，

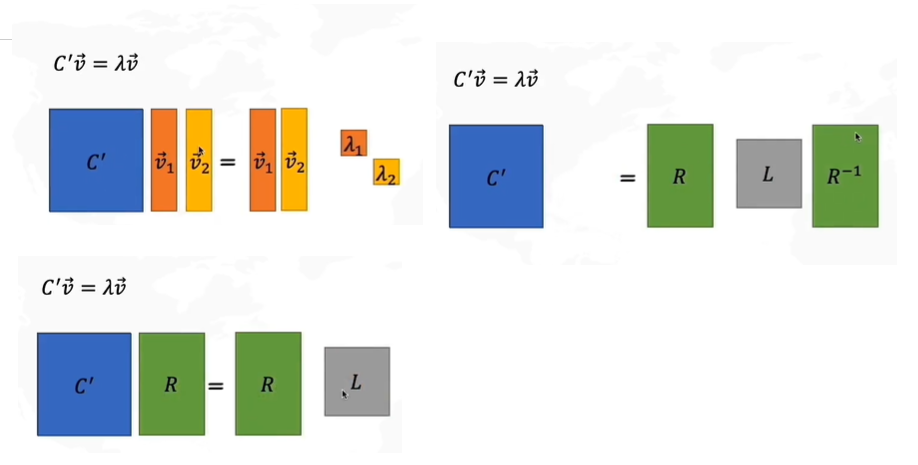
假设C′C'C′的特征值是λ\lambdaλ,我们来对其进行变形，由于是二维矩阵，所以有两个特征值，我们把特征值v1v2v_1v_2v1​v2​看作矩阵R,λ\lambdaλ看作矩阵L，得到如上图所示的矩阵变换。

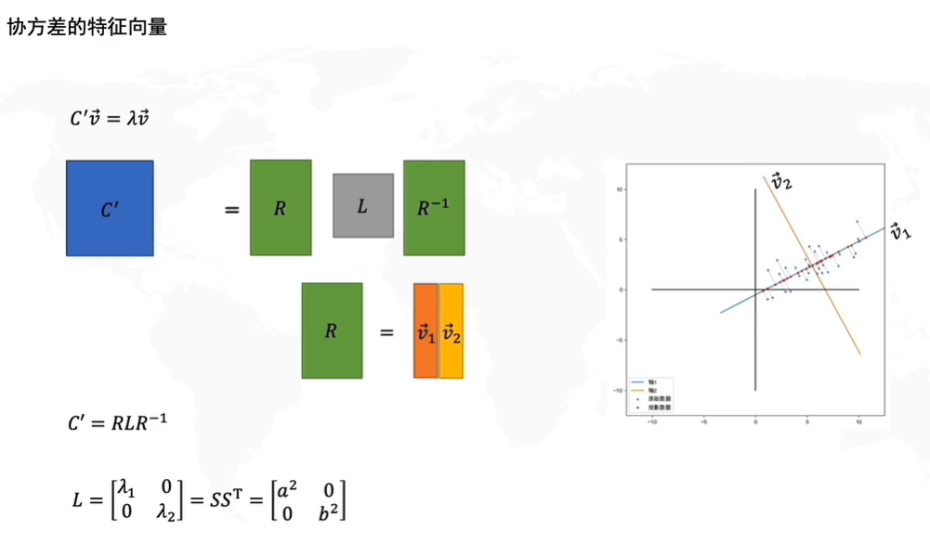
因此变换后的协方差矩阵C′=RLR−1C'=RLR^{-1}C′=RLR−1就相当于C′=特征向量∗特征值矩阵∗特征向量的转置C'=特征向量*特征值矩阵*特征向量的转置C′=特征向量∗特征值矩阵∗特征向量的转置
由于协方差代表了两个坐标的相关度，就相当于我们要求的线性变换后的矩阵D′D'D′其PCA的横轴PC1为第一列特征向量v⃗1\vec v_1v1​,而纵轴PC2就为v⃗2\vec v_2v2​,而L这个特征值矩阵代表了在白数据的xy方向上进行拉伸的倍数a,ba,ba,b的平方，λ1=a2,λ2=b2\lambda_1=a^2,\lambda_2=b^2λ1​=a2,λ2​=b2。为什么会这样呢？

重要思考！

协方差和方差存在着什么关系？这一点我们需要特别指出，我们之前说过协方差代表了数据在斜线上的传播关系，而方差代表了数据在x轴或者y轴上的传播关系。也就是说，方差和协方差是负相关的，当数据在斜线上的传播相关越大，则在横轴纵轴上的传播相关越小，也就是说，当协方差达到最大的时候，x和y的方差=0！同理当方差达到最大的时候，协方差=0。

让我们思考一个问题：方差在什么时候能够达到最大？

当然是协方差=0的时候，此时数据在斜方向上不相关，但是我们能不能直接确定一个最大方差？

或者我们换一个提问，能不能存在一个协方差矩阵，使得数据仅仅在轴方向上变换？

或者有没有一个矩阵，能使得线性变换相当于向量的拉伸？

魔法解开了，答案是特征向量！当数轴是特征向量，应用的矩阵相当于特征值的时候，Av⃗=λv⃗A\vec v=\lambda \vec vAv=λv,能够满足我们的条件！因此方差在什么时候能取到最大？也就是方差=λ\lambdaλ,协方差=0的时候！

现在再让我们看看这个公式

现在我们理解了，此时白数据的x轴就是v⃗1\vec v_1v1​,y轴就是v⃗2\vec v_2v2​，那么要使得方差最大，所以特征矩阵就是L=SST=[a200b2]L=SS^T=\begin{bmatrix} a^2 & 0 \\ 0& b^2 \end{bmatrix}L=SST=[a20​0b2​]

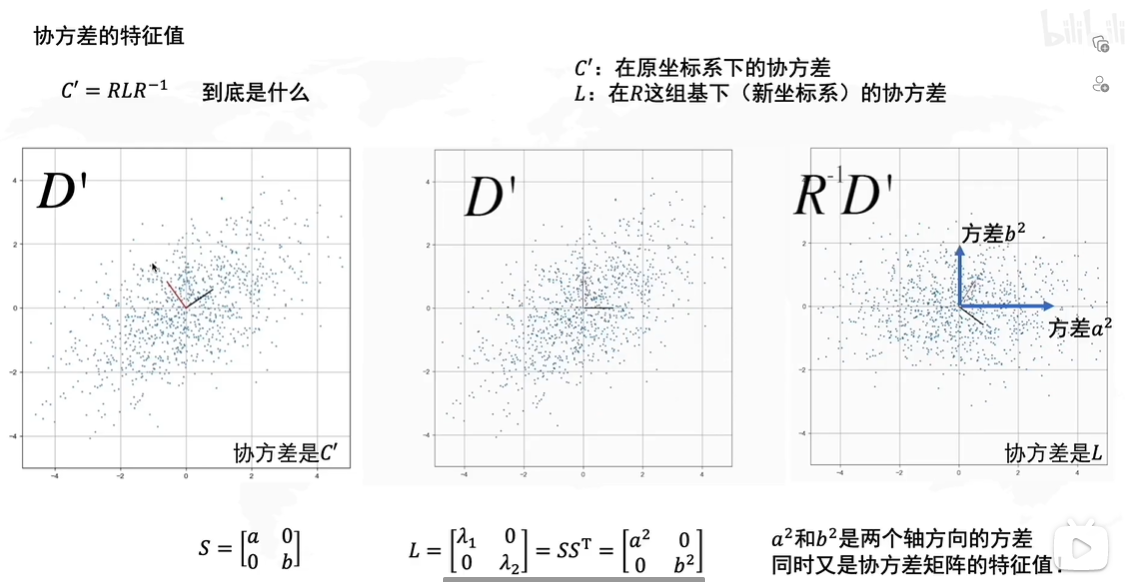
C′C'C′是D′D'D′的协方差，LLL是D′D'D′中用红蓝线画出的新坐标系下的协方差，我们对D′D'D′应用一下R−1R^{-1}R−1将其旋转回去，这样坐标就回归到了白数据的坐标（后两张图的红蓝坐标轴是将原点重新换到新坐标后的图片，后两张的红蓝坐标相当于新建的标准笛卡尔坐标系，与第一张图的红蓝轴不是同一个东西，由于网格没有对应发生变换所以可能看的有点迷糊），方差就代表了在白数据轴方向的拉伸倍数λ\lambdaλ，实际上此处的方差方向才是第一张图上的红蓝轴方向。

因此，PCA的方法实际上是将变换后的特征向量作为PC轴的方法，其方差最大的时候也就是对应协方差矩阵C=RLR−1C=RLR^{-1}C=RLR−1,相当于把特征方向旋转到标准坐标系上再应用LLL的特征值变换。

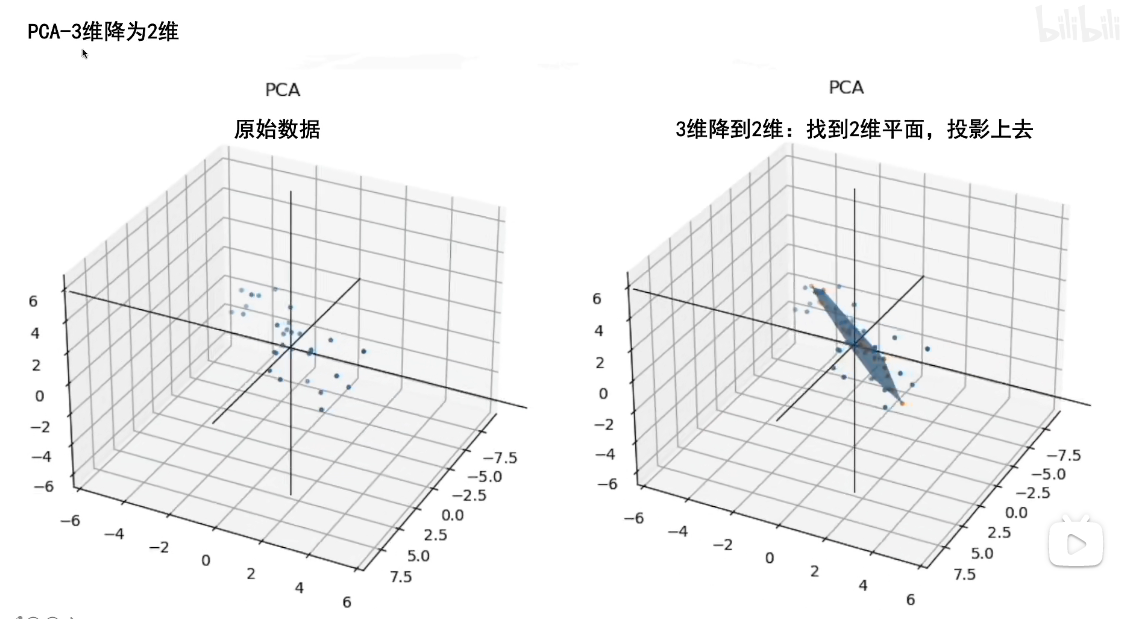
此外，三维降二维的PCA和我们刚才讲的类似，只不过我们要寻找的不止PC1，三维降二维是想让数据投影到我们寻找到的平面，所以我们寻找到方差最大的轴PC1之后，还需要寻找到过原点垂直于PC1且方差最大的PC2。在找到这两个轴后，PC3是一条过原点且同时垂直于PC1和PC2的轴，因此是唯一确定的。

置信椭圆

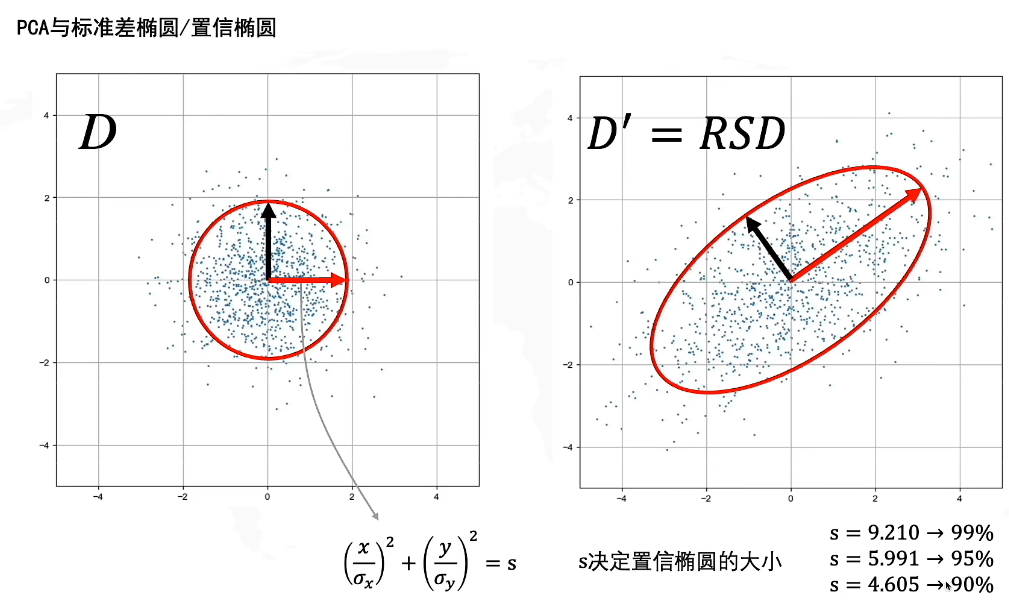
置信椭圆就是我们之前提到的置信域，它代表了一个搜索的区间范围。

在白噪声上的置信域是一个圆形，当我们对D进行了线性变换后，置信域被拉伸成了一个椭圆，由于是整体进行了变换，因此无论是变换前还是变换后，置信椭圆内包含的点的比例依旧是不变的，也就是若D中的s包含了95%的点，D’中的s依旧包含95%的点。置信椭圆的大小由s决定，可以查表得。

PCA的缺点

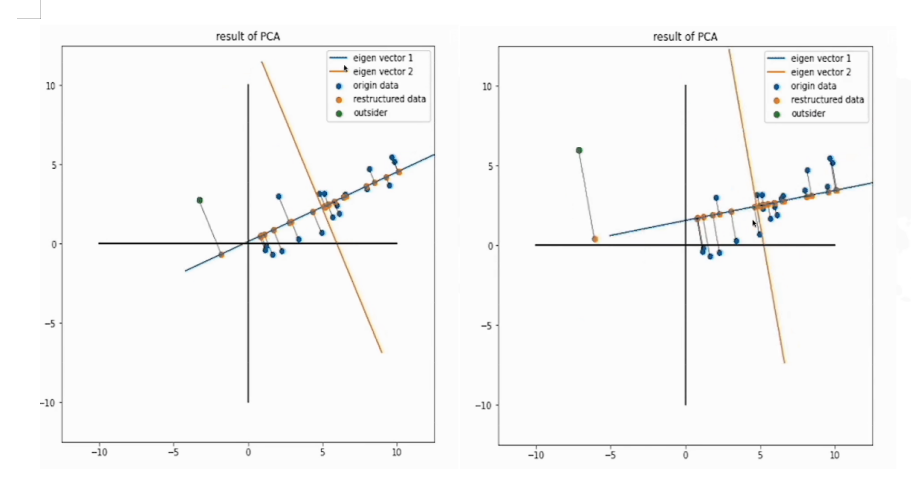
PCA相较于其他降维算法，的一个缺点就是离群点对于整体的影响较大，

PCA主成分与SVD的关系

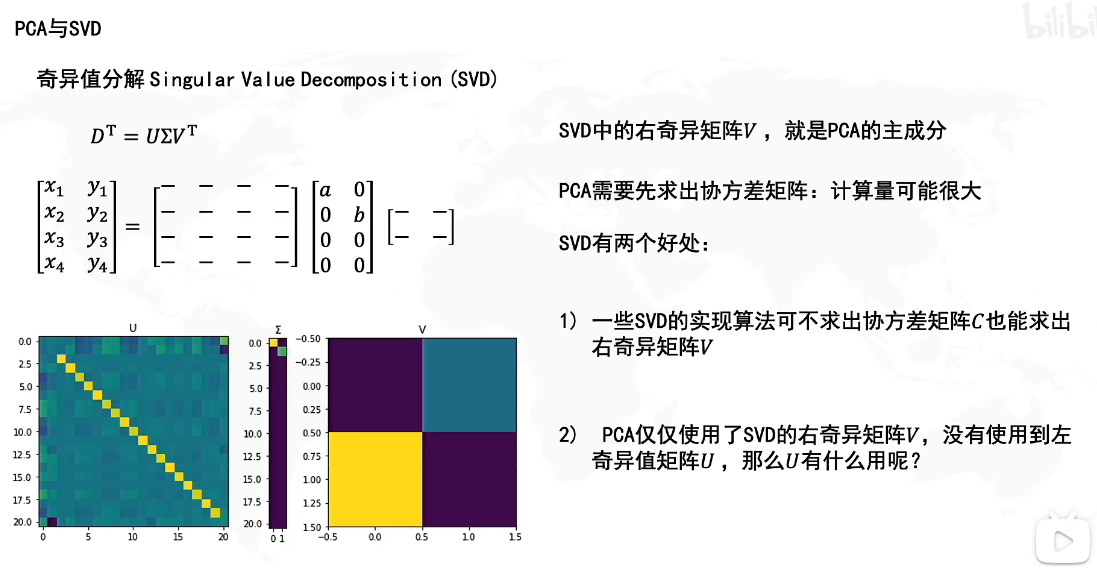
我们知道V是MTMM^TMMTM的特征向量，而PCA主成分的方向是协方差矩阵C=1n−1D′TD′C=\frac{1}{n-1}{D'}^TD'C=n−11​D′TD′的特征向量，因此二者的特征向量是同一个方向上的不同大小的向量，所以SVD的V就是PCA主成分的方向。

SVD的U矩阵是MMTMM^TMMT的特征向量，U的作用就是SVD里讲的，用三个矩阵压缩存储原矩阵。奇异值分解中的Σ\SigmaΣ奇异值选择其实就相当于PCA中的主成分选择，因此在这两式子中，特征值矩阵的对角元素个数就代表了保存的维度数量。

此外，奇异值分解相较于PCA，只需知道原矩阵M即可计算出U，V了，不需要计算协方差矩阵，而PCA需要先计算出协方差矩阵才能计算出新矩阵D′D'D′，因此相对而言SVD应该更高效。