第15章 局部波动率的影响
这学期会时不时更新一下伊曼纽尔·德曼(Emanuel Derman) 教授与迈克尔B.米勒(Michael B. Miller)的《The Volatility Smile》这本书,本意是协助导师课程需要,发在这里有意的朋友们可以学习一下,思路不一定够清晰且由于分工原因我是从书本第13章写起,还请大家见谅。
第15章 局部波动率的影响
局部波动率的DUPIRE公式
在第11章中曾推导过Breeden-Lizenberger公式:
p(S,t,K,T)=er(T−t)∂2C(S,t,K,T)∂K2p(S,t,K,T)=e^{r(T-t)}\frac{\partial^2C(S,t,K,T)}{\partial K^2} p(S,t,K,T)=er(T−t)∂K2∂2C(S,t,K,T)
其中,C(S,t,K,T)C(S,t,K,T)C(S,t,K,T) 表示行权价为 KKK、到期日为 TTT 的标准看涨期权在 ttt 时刻的市场价格,∂2C/∂K2\partial^2C/\partial K^2∂2C/∂K2 表示价差无限小的蝶式期权组合,p(S,t,K,T)p(S,t,K,T)p(S,t,K,T) 表示在 ttt 时刻、标的股票价格为 SSS 时,对应的在到期日 TTT 股票价格变为 KKK 的风险中性概率密度函数
下面给出Breeden-Lizenberger公式的推导:
假设有一个欧式衍生品,标的资产是 S,到期日为 TTT,只要我们知道在 TTT 时刻所有 STS_TST 价格下伪概率 p(S,t,ST,T)p(S,t,S_T,T)p(S,t,ST,T) 的值,那么我们就可以计算在到期日前的任意 ttt 时点该衍生品的价值,下面计算 p(S,t,ST,T)p(S,t,S_T,T)p(S,t,ST,T) :
假设有一个标准欧式看涨期权,在到期日 TTT 的损益为 max(ST−K,0)\max(S_T-K,0)max(ST−K,0),其在 ttt 时点的价格表示为 C(S,t,K,T)C(S,t,K,T)C(S,t,K,T),于是有:
C(St,t,K,T)=e−r(T−t)∫K∞p(S,t,ST,T)(ST−K)dSTC(S_t,t,K,T)=e^{-r(T-t)}\int_K^\infin p(S,t,S_T,T)(S_T-K)dS_T C(St,t,K,T)=e−r(T−t)∫K∞p(S,t,ST,T)(ST−K)dST
两边对 KKK 求导可得:
∂C(S,t,K,T)∂K=−e−r(T−t)∫K∞p(S,t,ST,T)dST\frac{\partial C(S,t,K,T)}{\partial K}=-e^{-r(T-t)}\int_K^\infin p(S,t,S_T,T)dS_T ∂K∂C(S,t,K,T)=−e−r(T−t)∫K∞p(S,t,ST,T)dST
再次对 KKK 进行二次微分求导可得:
∂2C(S,t,K,T)∂K2=−e−r(T−t)p(S,t,K,T)p(S,t,K,T)=er(T−t)∂2C(S,t,K,T)∂K2\frac{\partial^2C(S,t,K,T)}{\partial K^2}=-e^{-r(T-t)}p(S,t,K,T)\\ p(S,t,K,T)=e^{r(T-t)}\frac{\partial^2C(S,t,K,T)}{\partial K^2} ∂K2∂2C(S,t,K,T)=−e−r(T−t)p(S,t,K,T)p(S,t,K,T)=er(T−t)∂K2∂2C(S,t,K,T)
Breeden-Lizenberger公式不需要任何模型假设条件
相类似的,将要推导的Dupire公式描述的就是上一章提到的局部波动率与标准期权价格对行权价 KKK 和到期日 TTT 的偏微分之间的关系
假设无风险利率和股息率等于0,Dupire公式可以表示为:
σ2(K,T)2=∂C(S,t,K,T)∂TK2∂2C(S,t,K,T)∂K2\frac{\sigma^2(K,T)}{2}=\frac{\frac{\partial C(S,t,K,T)}{\partial T}}{K^2\frac{\partial^2C(S,t,K,T)}{\partial K^2}} 2σ2(K,T)=K2∂K2∂2C(S,t,K,T)∂T∂C(S,t,K,T)
这里的 σ(K,T)\sigma(K,T)σ(K,T) 是指在未来某时刻 TTT,股票价格为 KKK 时的局部波动率,该局部波动率对应的是更早一些的时刻 ttt,股票价格为 SSS 时的期权价格
如果无风险利率 r≠0r\neq0r=0,那么Dupire公式可以表示为:
σ2(K,T)2=∂C(S,t,K,T)∂T+rK∂C(S,t,K,T)∂KK2∂2C(S,t,K,T)∂K2\frac{\sigma^2(K,T)}{2}=\frac{\frac{\partial C(S,t,K,T)}{\partial T}+rK\frac{\partial C(S,t,K,T)}{\partial K}}{K^2\frac{\partial^2C(S,t,K,T)}{\partial K^2}} 2σ2(K,T)=K2∂K2∂2C(S,t,K,T)∂T∂C(S,t,K,T)+rK∂K∂C(S,t,K,T)
理解公式
考虑无风险利率等于0的情况,此时
p(S,t,K,T)=∂2C(S,t,K,T)∂K2p(S,t,K,T)=\frac{\partial^2C(S,t,K,T)}{\partial K^2} p(S,t,K,T)=∂K2∂2C(S,t,K,T)
∂2C(S,t,K,T)∂K2\dfrac{\partial^2C(S,t,K,T)}{\partial K^2}∂K2∂2C(S,t,K,T) 就是Breeden-Lizenberger公式中的风险中性概率密度函数 p(S,t,K,T)p(S,t,K,T)p(S,t,K,T),这个密度函数可以看作一个价差无限小的蝶式期权组合价格极限值
同时,由于:
∂C(S,t,K,T)∂T=limdT→0C(S,t,K,T+dT)−C(S,t,K,T)dT\frac{\partial C(S,t,K,T)}{\partial T}=\lim_{dT\to0}\frac{C(S,t,K,T+dT)-C(S,t,K,T)}{dT} ∂T∂C(S,t,K,T)=dT→0limdTC(S,t,K,T+dT)−C(S,t,K,T)
所以 ∂C(S,t,K,T)∂T\dfrac{\partial C(S,t,K,T)}{\partial T}∂T∂C(S,t,K,T) 可以看作 1/dT1/dT1/dT 份时间价格无限小的跨期期权组合价格极限值
下面分析跨期期权组合的变动情况,C(S,t,K,T+dT)−C(S,t,K,T)C(S,t,K,T+dT)-C(S,t,K,T)C(S,t,K,T+dT)−C(S,t,K,T),其中在时刻 TTT,近期期权到期,此时股票价格 S=STS=S_TS=ST。有三种可能性:ST≤K,ST≈K,ST≥KS_T\leq K,S_T\approx K,S_T\geq KST≤K,ST≈K,ST≥K
- ST≤KS_T\leq KST≤K,在到期日近期期权的价值等于0,且对于一个无限小的时间间隔 dTdTdT,远期期权的价值也接近于0
- ST≥KS_T\geq KST≥K,相似的,两个期权都处于实值状态,且价值相等
在上述两种情况下,当 dTdTdT 趋近于0时,跨期期权组合的价值等于0
而当 ST=KS_T=KST=K 时,近期期权在到期日处于平值状态,价值等于0,而远期期权价值为正,并且局部波动率 σ(K,T)\sigma(K,T)σ(K,T) 会引导股票价格向实值区间变动,于是跨期期权组合价值为正。因此,在 dT→0dT\to0dT→0 时,只有当 ST≈KS_T\approx KST≈K 时,1/dT1/dT1/dT 份跨期期权组合的价值为正,决定该组合价值的波动率就是局部波动率 σ(K,T)\sigma(K,T)σ(K,T)
我们将简短证明,间隔期间无限小的跨期期权组合的价值实际上是与局部波动率的平方 σ2(K,T)\sigma^2(K,T)σ2(K,T) 成比例关系。先假设这一结论成立,我们就有
C(S,t,K,T+dT)−C(S,t,K,T)∝p(S,t,K,T)σ2(K,T)dTC(S,t,K,T+dT)−C(S,t,K,T)∝∂2C(S,t,K,T)∂K2σ2(K,T)dTC(S,t,K,T+dT)−C(S,t,K,T)dT∝∂2C(S,t,K,T)∂K2σ2(K,T)dT→0:∂C(S,t,K,T)∂T∝∂2C(S,t,K,T)∂K2σ2(K,T)σ2(K,T)∝∂C(S,t,K,T)∂T∂2C(S,t,K,T)∂K2C(S,t,K,T+dT)-C(S,t,K,T)\propto p(S,t,K,T)\sigma^2(K,T)dT\\ C(S,t,K,T+dT)-C(S,t,K,T)\propto \frac{\partial^2C(S,t,K,T)}{\partial K^2}\sigma^2(K,T)dT\\ \frac{C(S,t,K,T+dT)-C(S,t,K,T)}{dT}\propto \frac{\partial^2C(S,t,K,T)}{\partial K^2}\sigma^2(K,T)\\dT\to0:\frac{\partial C(S,t,K,T)}{\partial T}\propto \frac{\partial^2C(S,t,K,T)}{\partial K^2}\sigma^2(K,T)\\ \sigma^2(K,T)\propto \frac{\frac{\partial C(S,t,K,T)}{\partial T}}{\frac{\partial^2C(S,t,K,T)}{\partial K^2}} C(S,t,K,T+dT)−C(S,t,K,T)∝p(S,t,K,T)σ2(K,T)dTC(S,t,K,T+dT)−C(S,t,K,T)∝∂K2∂2C(S,t,K,T)σ2(K,T)dTdTC(S,t,K,T+dT)−C(S,t,K,T)∝∂K2∂2C(S,t,K,T)σ2(K,T)dT→0:∂T∂C(S,t,K,T)∝∂K2∂2C(S,t,K,T)σ2(K,T)σ2(K,T)∝∂K2∂2C(S,t,K,T)∂T∂C(S,t,K,T)
这是局部波动率模型一个非常有吸引力的特点,那就是局部波动率与两个最常用的期权交易策略的比值密切相关。如果市场上有足够的跨期期权组合和蝶式期权组合的信息,我们就可以确定局部波动率曲面
若无风险利率不等于0:
σ2(K,T)2=∂C(S,t,K,T)∂T+rK∂C(S,t,K,T)∂KK2∂2C(S,t,K,T)∂K2∂C(S,t,K,T)∂T+rK∂C(S,t,K,T)∂K−σ2(K,T)2K2∂2C(S,t,K,T)∂K2=0\frac{\sigma^2(K,T)}{2}=\frac{\frac{\partial C(S,t,K,T)}{\partial T}+rK\frac{\partial C(S,t,K,T)}{\partial K}}{K^2\frac{\partial^2C(S,t,K,T)}{\partial K^2}}\\ \frac{\partial C(S,t,K,T)}{\partial T}+rK\frac{\partial C(S,t,K,T)}{\partial K}-\frac{\sigma^2(K,T)}{2}K^2\frac{\partial^2C(S,t,K,T)}{\partial K^2}=0 2σ2(K,T)=K2∂K2∂2C(S,t,K,T)∂T∂C(S,t,K,T)+rK∂K∂C(S,t,K,T)∂T∂C(S,t,K,T)+rK∂K∂C(S,t,K,T)−2σ2(K,T)K2∂K2∂2C(S,t,K,T)=0
上式类似于BSM等式,但是更加严格,其局部波动率模型只对普通欧式看涨期权或者看跌期权成立,将在下节做出证明
Dupire公式的价值在于,它可以告诉你如何通过一个标准期权的市场价格得到某特定的局部波动率函数 σ(K,T)\sigma(K,T)σ(K,T)。知道了所有 KKK 和 TTT 的局部波动率函数 σ(K,T)\sigma(K,T)σ(K,T),就可以建立一个包含这些局部波动率函数的隐含(波动率)树形图,并以此来计算奇异期权的价值,并且对标准期权进行对冲
DUPIRE公式的二叉树推导式
σ2(K,T)2=∂C(S,t,K,T)∂TK2∂2C(S,t,K,T)∂K2\frac{\sigma^2(K,T)}{2}=\frac{\frac{\partial C(S,t,K,T)}{\partial T}}{K^2\frac{\partial^2C(S,t,K,T)}{\partial K^2}} 2σ2(K,T)=K2∂K2∂2C(S,t,K,T)∂T∂C(S,t,K,T)
在推导过程中用到了二叉树模型的相关理论框架,并且假设利率和股息率等于0
树形图
首先建立一个Jarrow-Rudd树形图,每次上行下行的概率都等于 1/21/21/2。在这个树形图中,令每个阶段的时间间隔都等于 dT/2dT/2dT/2,这会使得跨期期权的估值更加简便,假设有个节点满足对应条件 (K,T)(K,T)(K,T),如下图所示:
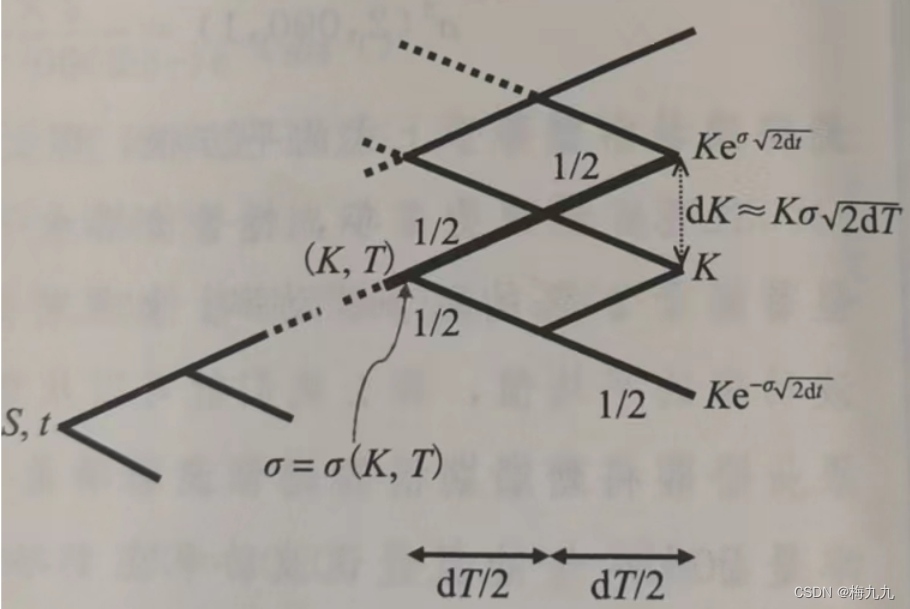
Dupire公式的分子项与一个跨期期权组合价值成比例关系,该跨期期权包括买入一个行权价和期限分别为 (K,T+dT)(K,T+dT)(K,T+dT) 的看涨期权以及卖出一个行权价和期限分别为 (K,T)(K,T)(K,T) 的看涨期权。用 pK,Tp_{K,T}pK,T 表示从条件 (S,t)(S,t)(S,t) 移动到 (K,T)(K,T)(K,T) 的风险中性概率
下面考虑,在时点 TTT,树形图中的各个节点对 (K,T+dT)(K,T+dT)(K,T+dT) 看涨期权以及 (K,T)(K,T)(K,T) 看涨期权的价值分别贡献了多少
- 在 TTT 时刻,只要节点股票价格 ST′S_T'ST′ 低于 KKK 水平,那么 (K,T)(K,T)(K,T) 看涨期权就是都处于虚值状态。在此基础上,到了 T+dTT+dTT+dT 时刻,节点股票价格变为 ST+dT′S'_{T+dT}ST+dT′,于是 (K,T+dT)(K,T+dT)(K,T+dT) 看涨期权的价值等于0。因此,在 TTT 时刻所有股票价格低于 KKK 水平的节点,对跨期期权组合的价值都没有影响
- 在到期日 TTT 时刻,股票价格 ST′S_T'ST′ 高于 KKK 水平的任意一个节点,对 (K,T)(K,T)(K,T) 看涨期权的价值贡献都是 (ST′−K)(S_T'-K)(ST′−K)。在 T+dTT+dTT+dT 时刻,该节点会衍生出3个平值或者实值状态的节点,对应的股票价格为 ST+dT′S'_{T+dT}ST+dT′。因为所有的这些节点都是平值或者实值状态,于是我们可以证明,在 T+dTT+dTT+dT 时,(K,T+dT)(K,T+dT)(K,T+dT) 看涨期权在这3个节点对应的价值 (ST+dT′−K)(S'_{T+dT}-K)(ST+dT′−K) 的预期折现值就等于在 TTT 时,(K,T)(K,T)(K,T) 看涨期权在节点 ST′S_T'ST′ 的价值 (ST′−K)(S_T'-K)(ST′−K),节点 ST′S_T'ST′ 也是后3个节点的起点。因此,在 TTT 时刻,所有股票价格低于 KKK 水平的节点,对于跨期期权组合的价值都没有影响
- 考虑节点 (K,T)(K,T)(K,T) 本身。该节点本身就代表一个行权价为 KKK,期限为 TTT 的平值看涨期权,因此对于 (K,T)(K,T)(K,T) 看涨期权的价值没有影响。两个时间间隔阶段之后,在 T+dTT+dTT+dT 时点,该节点衍生出3个节点,如上图所示。对于行权价为 KKK,期限为 (T+dT)(T+dT)(T+dT) 的看涨期权来说,较低的两个节点分别处于虚值状态和平值状态,价值等于0。在3个节点中最高的节点,也就是股价等于 Keσ2ΔTKe^{\sigma\sqrt{2\Delta T}}Keσ2ΔT 时,行权价为 KKK 的看涨期权的价值就为正数。到达该节点的概率等于 1/4×pK,T1/4\times p_{K,T}1/4×pK,T
从 (K,T)(K,T)(K,T) 节点出发,沿着树形图,后续节点中有的会对 (K,T+dT)(K,T+dT)(K,T+dT) 看涨期权的价值有影响,而这些节点恰恰对 (K,T)(K,T)(K,T) 看涨期权的价值没有影响。除此之外,其他所有节点对两个看涨期权价值的影响都是相等的。因此跨期期权的价值就完全取决于上图中的粗线段所描述的转换路径。我们可以计算这个值是多少。每个时间间隔阶段等于 dT/2dT/2dT/2,于是上行参数就等于:
u=σdT2u=\sigma\sqrt{\frac{dT}{2}} u=σ2dT
其中 σ\sigmaσ 是局部波动率 σ(K,T)\sigma(K,T)σ(K,T) 的简写,从节点 (K,T)(K,T)(K,T) 出发,连续向上运动两次最高节点对应的股票价格等于:
S=Ke2u=Keσ2dTS=Ke^{2u}=Ke^{\sigma\sqrt{2dT}} S=Ke2u=Keσ2dT
跨期期权组合在 (T+dT)(T+dT)(T+dT) 时刻的价值就等于:
dK≡Keσ2dT−K≈Kσ2dTdK\equiv Ke^{\sigma\sqrt{2dT}}-K\approx K\sigma\sqrt{2dT} dK≡Keσ2dT−K≈Kσ2dT
在时点 ttt,假设无风险利率等于0,那么跨期期权组合的风险中性价值就等于该损益乘以实现该损益的风险中性概率,于是:
C(S,t,K,T+dT)−C(S,t,K,T)=14pK,TdK∂C(S,t,K,T)∂T≈C(S,t,K,T+dT)−C(S,t,K,T)dT=14pK,TdKdTC(S,t,K,T+dT)-C(S,t,K,T)=\frac{1}{4}p_{K,T}dK\\ \frac{\partial C(S,t,K,T)}{\partial T}\approx\frac{C(S,t,K,T+dT)-C(S,t,K,T)}{dT}=\frac{1}{4}p_{K,T}\frac{dK}{dT} C(S,t,K,T+dT)−C(S,t,K,T)=41pK,TdK∂T∂C(S,t,K,T)≈dTC(S,t,K,T+dT)−C(S,t,K,T)=41pK,TdTdK
蝶式价差期权组合
Dupire公式的分母与价差无限小的蝶式期权组合价值成比例关系:
C(S,t,K−dK,T)−2C(S,t,K,T)+C(S,t,K+dK,T)C(S,t,K-dK,T)-2C(S,t,K,T)+C(S,t,K+dK,T) C(S,t,K−dK,T)−2C(S,t,K,T)+C(S,t,K+dK,T)
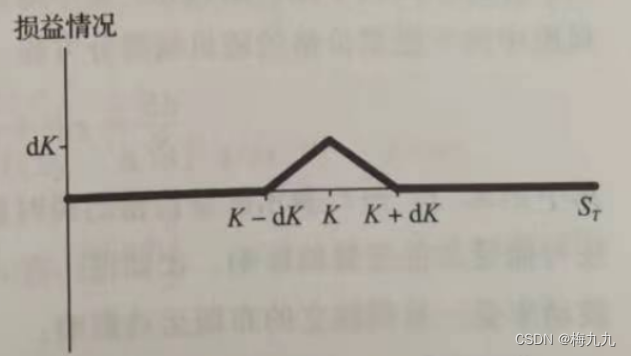
上图展示了这个蝶式价差期权组合的损益情况,在 TTT 时刻,如果股票价格恰好等于节点 KKK,那么组合的收益就等于 dKdKdK,在相邻节点,组合的损益等于0
之前曾经定义过离散概率 pK,Tp_{K,T}pK,T,该概率约定,在节点 (K,T)(K,T)(K,T),组合将支付1美元,因此该概率就等于 1/dK1/dK1/dK 份价差无限小的蝶式期权组合的价值,于是,在极限条件 dK→0dK\to0dK→0 时:
pK,T=C(S,t,K−dK,T)−2C(S,t,K,T)+C(S,t,K+dK,T)dK=C(S,t,K+dK,T)−C(S,t,K,T)dK−C(S,t,K,T)−C(S,t,K−dK,T)dK≈∂C(S,t,K,T)∂K−∂C(S,t,K−dK,T)∂K≈∂2C(S,t,K,T)∂K2dKp_{K,T}=\frac{C(S,t,K-dK,T)-2C(S,t,K,T)+C(S,t,K+dK,T)}{dK}\\=\frac{C(S,t,K+dK,T)-C(S,t,K,T)}{dK}-\frac{C(S,t,K,T)-C(S,t,K-dK,T)}{dK}\\\approx\frac{\partial C(S,t,K,T)}{\partial K}-\frac{\partial C(S,t,K-dK,T)}{\partial K}\\\approx\frac{\partial^2C(S,t,K,T)}{\partial K^2}dK pK,T=dKC(S,t,K−dK,T)−2C(S,t,K,T)+C(S,t,K+dK,T)=dKC(S,t,K+dK,T)−C(S,t,K,T)−dKC(S,t,K,T)−C(S,t,K−dK,T)≈∂K∂C(S,t,K,T)−∂K∂C(S,t,K−dK,T)≈∂K2∂2C(S,t,K,T)dK
于是上一节最后的等式可以写成:
∂C(S,t,K,T)∂T=14pK,TdKdT=14∂2C(S,t,K,T)∂K2dK2dT\frac{\partial C(S,t,K,T)}{\partial T}=\frac{1}{4}p_{K,T}\frac{dK}{dT}=\frac{1}{4}\frac{\partial^2C(S,t,K,T)}{\partial K^2}\frac{dK^2}{dT} ∂T∂C(S,t,K,T)=41pK,TdTdK=41∂K2∂2C(S,t,K,T)dTdK2
又因为 dK=Kσ2dTdK=K\sigma\sqrt{2dT}dK=Kσ2dT,于是有:
∂C(S,t,K,T)∂T=12σ2K2∂2C(S,t,K,T)∂K2→σ2(K,T)2=∂C(S,t,K,T)∂TK2∂2C(S,t,K,T)∂K2\frac{\partial C(S,t,K,T)}{\partial T}=\frac{1}{2}\sigma^2K^2\frac{\partial^2C(S,t,K,T)}{\partial K^2}\\\to\frac{\sigma^2(K,T)}{2}=\frac{\frac{\partial C(S,t,K,T)}{\partial T}}{K^2\frac{\partial^2C(S,t,K,T)}{\partial K^2}} ∂T∂C(S,t,K,T)=21σ2K2∂K2∂2C(S,t,K,T)→2σ2(K,T)=K2∂K2∂2C(S,t,K,T)∂T∂C(S,t,K,T)
这就是当无风险利率等于0时,局部波动率的Dupire公式
DUPIRE公式的严格证明
下面给出更为严格的证明
首先给出风险中性条件下股票价格的随机偏微分方程如下:
dSS=rdt+σ(S,t,...)dZ\frac{dS}{S}=rdt+\sigma(S,t,...)dZ SdS=rdt+σ(S,t,...)dZ
其中 σ(S,t,...)\sigma(S,t,...)σ(S,t,...) 表示股票价格的瞬时波动率,除了 S,tS,tS,t 之外可能还受其他变量的影响
在 ttt 时刻,一个行权价为 KKK,期限为 TTT 的普通欧式看涨期权的价值为
C(S,t,K,T)=e−r(T−t)E[(ST−K)+]C(S,t,K,T)=e^{-r(T-t)}E[(S_T-K)_+] C(S,t,K,T)=e−r(T−t)E[(ST−K)+]
引入 Heaviside 方程 H(x)H(x)H(x) 以及 Dirac delta 方程 δ(x)\delta(x)δ(x):
H(x)={1,x≥00,x<0H(x)=\begin{cases}1,x\geq0\\0,x<0 \end{cases} H(x)={1,x≥00,x<0
Dirac delta 方程 δ(x)\delta(x)δ(x) 可看作是 Heaviside 函数的广义导数
于是看涨期权的价值可以表示为:
C(S,t,K,T)=e−r(T−t)E[(ST−K)H(ST−K)]C(S,t,K,T)=e^{-r(T-t)}E[(S_T-K)H(S_T-K)] C(S,t,K,T)=e−r(T−t)E[(ST−K)H(ST−K)]
对上式分别对 KKK 求一阶导和二阶导:
∂C(S,t,K,T)∂K=−e−r(T−t)E[H(ST−K)]∂2C(S,t,K,T)∂K2=e−r(T−t)E[δ(ST−K)]\frac{\partial C(S,t,K,T)}{\partial K}=-e^{-r(T-t)}E[H(S_T-K)]\\ \frac{\partial^2C(S,t,K,T)}{\partial K^2}=e^{-r(T-t)}E[\delta(S_T-K)] ∂K∂C(S,t,K,T)=−e−r(T−t)E[H(ST−K)]∂K2∂2C(S,t,K,T)=e−r(T−t)E[δ(ST−K)]
在 KKK 不变而 TTT 增加的情况下,要找到 C(S,t,K,T)C(S,t,K,T)C(S,t,K,T) 对 TTT 的总导数,我们需要考虑 dTdTdT 变动对 CCC 的影响,以及随机变量 STS_TST 变动对 CCC 的影响。因此:
dTC∣K=E[∂C∂TdT+∂C∂STdST+12∂2C∂ST2(dST)2]=E[−rCdT+e−r(T−t)H(ST−K)dST+12e−r(T−t)δ(ST−K)(dST)2]=e−r(T−t)E[−rer(T−t)CdT+H(ST−K)dST+12δ(ST−K)(dST)2]=e−r(T−t)E[−rer(T−t)CdT+H(ST−K)dST+12δ(ST−K)σ2(ST,T,...)ST2dT]d_TC|_K=E[\frac{\partial C}{\partial T}dT+\frac{\partial C}{\partial S_T}dS_T+\frac{1}{2}\frac{\partial^2C}{\partial S_T^2}(dS_T)^2]\\=E[-rCdT+e^{-r(T-t)}H(S_T-K)dS_T+\frac{1}{2}e^{-r(T-t)}\delta(S_T-K)(dS_T)^2]\\=e^{-r(T-t)}E[-re^{r(T-t)}CdT+H(S_T-K)dS_T+\frac{1}{2}\delta(S_T-K)(dS_T)^2]\\=e^{-r(T-t)}E[-re^{r(T-t)}CdT+H(S_T-K)dS_T+\frac{1}{2}\delta(S_T-K)\sigma^2(S_T,T,...)S_T^2dT] dTC∣K=E[∂T∂CdT+∂ST∂CdST+21∂ST2∂2C(dST)2]=E[−rCdT+e−r(T−t)H(ST−K)dST+21e−r(T−t)δ(ST−K)(dST)2]=e−r(T−t)E[−rer(T−t)CdT+H(ST−K)dST+21δ(ST−K)(dST)2]=e−r(T−t)E[−rer(T−t)CdT+H(ST−K)dST+21δ(ST−K)σ2(ST,T,...)ST2dT]
在最后一项中用 STS_TST 代替 KKK,可以得到:
dTC∣K=e−r(T−t)E[−rer(T−t)CdT+H(ST−K)dST+12δ(ST−K)σ2(ST,T,...)K2dT]d_TC|_K=e^{-r(T-t)}E[-re^{r(T-t)}CdT+H(S_T-K)dS_T+\frac{1}{2}\delta(S_T-K)\sigma^2(S_T,T,...)K^2dT] dTC∣K=e−r(T−t)E[−rer(T−t)CdT+H(ST−K)dST+21δ(ST−K)σ2(ST,T,...)K2dT]
将 C(S,t,K,T)=e−r(T−t)E[(ST−K)H(ST−K)]C(S,t,K,T)=e^{-r(T-t)}E[(S_T-K)H(S_T-K)]C(S,t,K,T)=e−r(T−t)E[(ST−K)H(ST−K)] 代入得:
dTC∣K=e−r(T−t)E[−r(ST−K)H(ST−K)dT+H(ST−K)dST+12δ(ST−K)σ2(ST,T,...)K2dT]d_TC|_K=e^{-r(T-t)}E[-r(S_T-K)H(S_T-K)dT+H(S_T-K)dS_T\\+\frac{1}{2}\delta(S_T-K)\sigma^2(S_T,T,...)K^2dT] dTC∣K=e−r(T−t)E[−r(ST−K)H(ST−K)dT+H(ST−K)dST+21δ(ST−K)σ2(ST,T,...)K2dT]
根据股票价格的随机偏微分方程,可以将 dSTdS_TdST 进行如下代替:
dTC∣K=e−r(T−t)E[−r(ST−K)H(ST−K)dT+H(ST−K)(STrdT+σ(ST,T,...)dZ)+12δ(ST−K)σ2(ST,T,...)K2dT]dTC∣K=e−r(T−t)E[rKH(ST−K)dT+12δ(ST−K)σ2(ST,T,...)K2dT]d_TC|_K=e^{-r(T-t)}E[-r(S_T-K)H(S_T-K)dT+H(S_T-K)(S_TrdT+\sigma(S_T,T,...)dZ)\\+\frac{1}{2}\delta(S_T-K)\sigma^2(S_T,T,...)K^2dT]\\ d_TC|_K=e^{-r(T-t)}E[rKH(S_T-K)dT+\frac{1}{2}\delta(S_T-K)\sigma^2(S_T,T,...)K^2dT] dTC∣K=e−r(T−t)E[−r(ST−K)H(ST−K)dT+H(ST−K)(STrdT+σ(ST,T,...)dZ)+21δ(ST−K)σ2(ST,T,...)K2dT]dTC∣K=e−r(T−t)E[rKH(ST−K)dT+21δ(ST−K)σ2(ST,T,...)K2dT]
我们之前有:
∂C(S,t,K,T)∂K=−e−r(T−t)E[H(ST−K)]∂2C(S,t,K,T)∂K2=e−r(T−t)E[δ(ST−K)]\frac{\partial C(S,t,K,T)}{\partial K}=-e^{-r(T-t)}E[H(S_T-K)]\\ \frac{\partial^2C(S,t,K,T)}{\partial K^2}=e^{-r(T-t)}E[\delta(S_T-K)] ∂K∂C(S,t,K,T)=−e−r(T−t)E[H(ST−K)]∂K2∂2C(S,t,K,T)=e−r(T−t)E[δ(ST−K)]
将上述左式作替换代入可得:
dTC∣K=−rK∂C(S,t,K,T)∂KdT+12∂2C(S,t,K,T)∂K2E[σ2(K,T,...)]K2dT∂C∂T∣K=−rK∂C(S,t,K,T)∂K+12∂2C(S,t,K,T)∂K2E[σ2(K,T,...)]K2E[σ2(K,T,...)]2=∂C∂T∣K+rK∂C(S,t,K,T)∂K∣TK2∂2C(S,t,K,T)∂K2∣Td_TC|_K=-rK\frac{\partial C(S,t,K,T)}{\partial K}dT+\frac{1}{2}\frac{\partial^2C(S,t,K,T)}{\partial K^2}E[\sigma^2(K,T,...)]K^2dT\\ \frac{\partial C}{\partial T}|_K=-rK\frac{\partial C(S,t,K,T)}{\partial K}+\frac{1}{2}\frac{\partial^2C(S,t,K,T)}{\partial K^2}E[\sigma^2(K,T,...)]K^2\\ \frac{E[\sigma^2(K,T,...)]}{2}=\frac{\frac{\partial C}{\partial T}|_K+rK\frac{\partial C(S,t,K,T)}{\partial K}|_T}{K^2\frac{\partial^2C(S,t,K,T)}{\partial K^2}|_T} dTC∣K=−rK∂K∂C(S,t,K,T)dT+21∂K2∂2C(S,t,K,T)E[σ2(K,T,...)]K2dT∂T∂C∣K=−rK∂K∂C(S,t,K,T)+21∂K2∂2C(S,t,K,T)E[σ2(K,T,...)]K22E[σ2(K,T,...)]=K2∂K2∂2C(S,t,K,T)∣T∂T∂C∣K+rK∂K∂C(S,t,K,T)∣T
上式也是Dupire公式。现在可以用未来在 KKK 价格水平和 TTT 时刻瞬时方差的平均数来表示广义局部方差 σ2(K,T)\sigma^2(K,T)σ2(K,T),该表达式还可以包括影响方差值的所有其他变量,即:
σ2(K,T)=E[σ2(K,T,...)]\sigma^2(K,T)=E[\sigma^2(K,T,...)] σ2(K,T)=E[σ2(K,T,...)]
局部波动率和隐含波动率之间的严格关系式及相关应用
当无风险利率和股息率都等于0的时候有如下关系:
σ2(K,T)2=∂C∂T∣KK2∂2C∂K2∣T\frac{\sigma^2(K,T)}{2}=\frac{\frac{\partial C}{\partial T}|_K}{K^2\frac{\partial^2C}{\partial K^2}|_T} 2σ2(K,T)=K2∂K2∂2C∣T∂T∂C∣K
若用 BSMBSMBSM 隐含波动率 Σ\SigmaΣ 来对期权进行估值,则有:
C(S,t,K,T)=CBSM(S,t,K,T,Σ(S,t,K,T))C(S,t,K,T)=C_{BSM}(S,t,K,T,\Sigma(S,t,K,T)) C(S,t,K,T)=CBSM(S,t,K,T,Σ(S,t,K,T))
在微分过程中运用链式法则,并且代人 BSM 模型中的各希腊字母参数,我们可以得到:
σ2(K,τ)=2∂Σ∂τ+ΣτK2[∂2Σ∂K2−d1τ(∂Σ∂K)2+1Σ(1Kτ+d1∂Σ∂K)2]τ=T−t,d1=1Στln(SK)+12Στ\sigma^2(K,\tau)=\frac{2\frac{\partial\Sigma}{\partial\tau}+\frac{\Sigma}{\tau}}{K^2[\frac{\partial^2\Sigma}{\partial K^2}-d_1\sqrt{\tau}(\frac{\partial\Sigma}{\partial K})^2+\frac{1}{\Sigma}(\frac{1}{K\sqrt{\tau}}+d_1\frac{\partial\Sigma}{\partial K})^2]}\\ \tau=T-t,d_1=\frac{1}{\Sigma\sqrt{\tau}}\ln(\frac{S}{K})+\frac{1}{2}\Sigma\sqrt{\tau} σ2(K,τ)=K2[∂K2∂2Σ−d1τ(∂K∂Σ)2+Σ1(Kτ1+d1∂K∂Σ)2]2∂τ∂Σ+τΣτ=T−t,d1=Στ1ln(KS)+21Στ
上式的局部波动率曲面公式 σ(K,T)\sigma(K,T)σ(K,T) 是用BSM隐含波动率来表示的,而不是用期权价格
在不存在斜度的条件下,隐含方差等于局部方差在期权有效期内的平均值
如果 Σ\SigmaΣ 跟行权价 KKK 无关,那么 σ(K,τ)\sigma(K,\tau)σ(K,τ) 也跟行权价无关,上式可以简化为:
σ2(τ)=2∂Σ∂τ+ΣτK2[1Σ(1Kτ)2]=2τΣ∂Σ∂τ+Σ2=∂∂τ(τΣ2)\sigma^2(\tau)=\frac{2\frac{\partial\Sigma}{\partial\tau}+\frac{\Sigma}{\tau}}{K^2[\frac{1}{\Sigma}(\frac{1}{K\sqrt{\tau}})^2]}\\=2\tau\Sigma\frac{\partial\Sigma}{\partial\tau}+\Sigma^2\\=\frac{\partial}{\partial\tau}(\tau\Sigma^2) σ2(τ)=K2[Σ1(Kτ1)2]2∂τ∂Σ+τΣ=2τΣ∂τ∂Σ+Σ2=∂τ∂(τΣ2)
对等式两侧进行积分可以得到:
∫0τσ2(u)du=τΣ2(τ)\int_0^\tau\sigma^2(u)du=\tau\Sigma^2(\tau) ∫0τσ2(u)du=τΣ2(τ)
从一个更广义的角度来看,当 Σ\SigmaΣ 跟行权价格无关的时候,远期方差的合计数就等于总的隐含方差
两倍定律回顾
假设局部波动率只受行权价格的影响,而不受到期日的影响:
Σ=Σ(K)∂Σ∂τ=0\Sigma=\Sigma(K)\\ \frac{\partial\Sigma}{\partial\tau}=0 Σ=Σ(K)∂τ∂Σ=0
同时,假设斜度跟 KKK 之间存在弱线性相关关系,这样我们就只需要保留与 ∂C/∂K\partial C/\partial K∂C/∂K 成比例关系的变量,而更高阶的 (∂C/∂K)2,∂2C/∂K2(\partial C/\partial K)^2,\partial^2C/\partial K^2(∂C/∂K)2,∂2C/∂K2 就可以忽略不计。于是:
σ2(K,T)=ΣτK2[1Σ(1Kτ+d1∂Σ∂K)2]=Σ2(1+d1Kτ∂Σ∂K)2σ(K,τ)=Σ(K)1+d1Kτ∂Σ∂K\sigma^2(K,T)=\frac{\frac{\Sigma}{\tau}}{K^2[\frac{1}{\Sigma}(\frac{1}{K\sqrt{\tau}}+d_1\frac{\partial\Sigma}{\partial K})^2]}=\frac{\Sigma^2}{(1+d_1K\sqrt{\tau}\frac{\partial\Sigma}{\partial K})^2}\\ \sigma(K,\tau)=\frac{\Sigma(K)}{1+d_1K\sqrt{\tau}\frac{\partial\Sigma}{\partial K}} σ2(K,T)=K2[Σ1(Kτ1+d1∂K∂Σ)2]τΣ=(1+d1Kτ∂K∂Σ)2Σ2σ(K,τ)=1+d1Kτ∂K∂ΣΣ(K)
当期权接近于平值状态,也就是当 K=S+ΔKK=S+\Delta KK=S+ΔK 时,我们就有:
d1≈ln(SK)Στ≈−ΔKS(Στ)≈−ΔKK(Στ)d_1\approx\frac{\ln(\frac{S}{K})}{\Sigma\sqrt{\tau}}\approx-\frac{\Delta K}{S(\Sigma\sqrt{\tau})}\approx-\frac{\Delta K}{K(\Sigma\sqrt{\tau})} d1≈Στln(KS)≈−S(Στ)ΔK≈−K(Στ)ΔK
于是对于领头阶就有:
σ(K)≈Σ(K)1−ΔKΣ∂Σ∂K≈Σ(K)(1+ΔKΣ∂Σ∂K)≈Σ(K)+ΔK∂Σ∂K\sigma(K)\approx\frac{\Sigma(K)}{1-\frac{\Delta K}{\Sigma}\frac{\partial\Sigma}{\partial K}}\approx\Sigma(K)(1+\frac{\Delta K}{\Sigma}\frac{\partial\Sigma}{\partial K})\approx\Sigma(K)+\Delta K\frac{\partial\Sigma}{\partial K} σ(K)≈1−ΣΔK∂K∂ΣΣ(K)≈Σ(K)(1+ΣΔK∂K∂Σ)≈Σ(K)+ΔK∂K∂Σ
其中 K=S+ΔKK=S+\Delta KK=S+ΔK,ΔK\Delta KΔK 表示股价与平值期权行权价的差异。因此:
σ(S+ΔK)≈Σ(S+ΔK)+ΔK∂Σ(S+ΔK)∂K\sigma(S+\Delta K)\approx\Sigma(S+\Delta K)+\Delta K\frac{\partial\Sigma(S+\Delta K)}{\partial K} σ(S+ΔK)≈Σ(S+ΔK)+ΔK∂K∂Σ(S+ΔK)
在 SSS 进行泰勒展开可得:
σ(S)+∂σ(S)∂SΔK≈Σ(S)+2∂Σ(S)∂SΔK\sigma(S)+\frac{\partial\sigma(S)}{\partial S}\Delta K\approx\Sigma(S)+2\frac{\partial\Sigma(S)}{\partial S}\Delta K σ(S)+∂S∂σ(S)ΔK≈Σ(S)+2∂S∂Σ(S)ΔK
于是有 σ(S)≈Σ(S)\sigma(S)\approx\Sigma(S)σ(S)≈Σ(S),且
∂∂Sσ(S)≈2(∂Σ∂K)∣K=S\frac{\partial}{\partial S}\sigma(S)\approx2(\frac{\partial\Sigma}{\partial K})|_{K=S} ∂S∂σ(S)≈2(∂K∂Σ)∣K=S
即:局部波动率随股票价格的变动速度是隐含波动率随行权价格的变动速度的两倍
当期限较短时,隐含波动率等于当前股价和行权价之间的局部波动率的调和平均数
对于一个正数序列,x1,x2,...,xnx_1,x_2,...,x_nx1,x2,...,xn,其调和平均数 μH\mu_HμH 的定义是:
μH=n1x1+1x2+...+1xn\mu_H=\frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+...+\frac{1}{x_n}} μH=x11+x21+...+xn1n
假设有一个连续随机变量,其正态密度函数为 f(x)f(x)f(x),那么其调和平均数就等于:
μH=1∫0∞1xf(x)dx\mu_H=\frac{1}{\int_0^\infin\frac{1}{x}f(x)dx} μH=∫0∞x1f(x)dx1
考虑之前推导过的下式:
σ2(K,τ)=2∂Σ∂τ+ΣτK2[∂2Σ∂K2−d1τ(∂Σ∂K)2+1Σ(1Kτ+d1∂Σ∂K)2]\sigma^2(K,\tau)=\frac{2\frac{\partial\Sigma}{\partial\tau}+\frac{\Sigma}{\tau}}{K^2[\frac{\partial^2\Sigma}{\partial K^2}-d_1\sqrt{\tau}(\frac{\partial\Sigma}{\partial K})^2+\frac{1}{\Sigma}(\frac{1}{K\sqrt{\tau}}+d_1\frac{\partial\Sigma}{\partial K})^2]} σ2(K,τ)=K2[∂K2∂2Σ−d1τ(∂K∂Σ)2+Σ1(Kτ1+d1∂K∂Σ)2]2∂τ∂Σ+τΣ
假设将等式右侧分子分母同时乘以 τ\tauτ,可得:
σ2(K,τ)=2τ∂Σ∂τ+ΣK2[τ∂2Σ∂K2−d1ττ(∂Σ∂K)2+1Σ(1K+d1τ∂Σ∂K)2]\sigma^2(K,\tau)=\frac{2\tau\frac{\partial\Sigma}{\partial\tau}+\Sigma}{K^2[\tau\frac{\partial^2\Sigma}{\partial K^2}-d_1\tau\sqrt{\tau}(\frac{\partial\Sigma}{\partial K})^2+\frac{1}{\Sigma}(\frac{1}{K}+d_1\sqrt{\tau}\frac{\partial\Sigma}{\partial K})^2]} σ2(K,τ)=K2[τ∂K2∂2Σ−d1ττ(∂K∂Σ)2+Σ1(K1+d1τ∂K∂Σ)2]2τ∂τ∂Σ+Σ
当 τ→0\tau\to0τ→0 时:
limτ→0σ2(K,τ)=ΣK2[1Σ(1K+d1τ∂Σ∂K)2]=Σ2(1+d1τK∂Σ∂K)2\lim_{\tau\to0}\sigma^2(K,\tau)=\frac{\Sigma}{K^2[\frac{1}{\Sigma}(\frac{1}{K}+d_1\sqrt{\tau}\frac{\partial\Sigma}{\partial K})^2]}=\frac{\Sigma^2}{(1+d_1\sqrt{\tau}K\frac{\partial\Sigma}{\partial K})^2} τ→0limσ2(K,τ)=K2[Σ1(K1+d1τ∂K∂Σ)2]Σ=(1+d1τK∂K∂Σ)2Σ2
其中:
d1τ=1Σln(SK)+12Στlimτ→0d1τ=1Σln(SK)d_1\sqrt{\tau}=\frac{1}{\Sigma}\ln(\frac{S}{K})+\frac{1}{2}\Sigma\tau\\ \lim_{\tau\to0}d_1\sqrt{\tau}=\frac{1}{\Sigma}\ln(\frac{S}{K}) d1τ=Σ1ln(KS)+21Σττ→0limd1τ=Σ1ln(KS)
代入得:
limτ→0σ2(K,τ)=Σ2(1+1Σln(SK)K∂Σ∂K)2σ(K)=limτ→0σ(K,τ)=Σ1+KΣln(SK)dΣdK\lim_{\tau\to0}\sigma^2(K,\tau)=\frac{\Sigma^2}{(1+\frac{1}{\Sigma}\ln(\frac{S}{K})K\frac{\partial\Sigma}{\partial K})^2}\\ \sigma(K)=\lim_{\tau\to0}\sigma(K,\tau)=\frac{\Sigma}{1+\frac{K}{\Sigma}\ln(\frac{S}{K})\frac{d\Sigma}{dK}} τ→0limσ2(K,τ)=(1+Σ1ln(KS)K∂K∂Σ)2Σ2σ(K)=τ→0limσ(K,τ)=1+ΣKln(KS)dKdΣΣ
令 x=ln(K/S)x=\ln(K/S)x=ln(K/S),于是有:
dΣdx=dΣ/(SK×1SdK)=KdΣdK\frac{d\Sigma}{dx}=d\Sigma/(\frac{S}{K}\times\frac{1}{S}dK)=K\frac{d\Sigma}{dK} dxdΣ=dΣ/(KS×S1dK)=KdKdΣ
于是,σ(K)\sigma(K)σ(K) 可以被改写为:
σ(K)=Σ1+KΣln(SK)dΣdK=Σ1−xΣdΣdx\sigma(K)=\frac{\Sigma}{1+\frac{K}{\Sigma}\ln(\frac{S}{K})\frac{d\Sigma}{dK}}=\frac{\Sigma}{1-\frac{x}{\Sigma}\frac{d\Sigma}{dx}} σ(K)=1+ΣKln(KS)dKdΣΣ=1−ΣxdxdΣΣ
令 V=1/ΣV=1/\SigmaV=1/Σ,于是:
dΣdx=−1V2dVdxσ(K)=Σ1−xΣdΣdx=1/V1+xV1V2dVdx=1V[1+xVdVdx]V+xdVdx=1σ(K)ddx(xV)=1σ(K)\frac{d\Sigma}{dx}=-\frac{1}{V^2}\frac{dV}{dx}\\ \sigma(K)=\frac{\Sigma}{1-\frac{x}{\Sigma}\frac{d\Sigma}{dx}}=\frac{1/V}{1+xV\frac{1}{V^2}\frac{dV}{dx}}=\frac{1}{V[1+\frac{x}{V}\frac{dV}{dx}]}\\ V+x\frac{dV}{dx}=\frac{1}{\sigma(K)}\\ \frac{d}{dx}(xV)=\frac{1}{\sigma(K)} dxdΣ=−V21dxdVσ(K)=1−ΣxdxdΣΣ=1+xVV21dxdV1/V=V[1+VxdxdV]1V+xdxdV=σ(K)1dxd(xV)=σ(K)1
此前,局部波动率 σ(K)\sigma(K)σ(K) 的表达式中,用到的参数是股票价格 KKK,现在我们将该参数转化为函数 ln(K/S)\ln(K/S)ln(K/S)。因此,当我们提到 σ(x)\sigma(x)σ(x) 的时候,我们指的仍然是跟之前一样的波动率数值,只是我们将参数换成了函数 x=ln(K/S)x=\ln(K/S)x=ln(K/S)。注意,在隐含波动率函数中,变量 KKK 表示行权价,而在局部波动率函数中,KKK 表示的是股票价格,这点非常重要。于是上式变成:
ddx(xV)=1σ(x)\frac{d}{dx}(xV)=\frac{1}{\sigma(x)} dxd(xV)=σ(x)1
对等式两侧同时积分,范围是从 x=0x=0x=0 到 x=ln(K/S)x=\ln(K/S)x=ln(K/S):
xV∣0ln(K/S)=∫0ln(K/S)1σ(x)dxln(KS)V(S,K)=∫0ln(KS)1σ(x)dxln(KS)Σ(KS)=∫0ln(KS)1σ(x)dxxV|_0^{\ln(K/S)}=\int_0^{\ln(K/S)}\frac{1}{\sigma(x)}dx\\ \ln(\frac{K}{S})V(S,K)=\int_0^{\ln(\frac{K}{S})}\frac{1}{\sigma(x)}dx\\ \frac{\ln(\frac{K}{S})}{\Sigma(\frac{K}{S})}=\int_0^{\ln(\frac{K}{S})}\frac{1}{\sigma(x)}dx xV∣0ln(K/S)=∫0ln(K/S)σ(x)1dxln(SK)V(S,K)=∫0ln(SK)σ(x)1dxΣ(SK)ln(SK)=∫0ln(SK)σ(x)1dx
假设当前股票价格为 SSS,某标准期权的行权价为 KKK,随着到期日临近,期权的隐含波动率函数 ln(K/S)\ln(K/S)ln(K/S) 就等于 S,KS,KS,K 之间所有股票价格 S′S'S′ 对应的局部波动率的调和平均数,其中局部波动率函数可以表示为 ln(S′/S)\ln(S'/S)ln(S′/S),范围是0到 ln(K/S)\ln(K/S)ln(K/S)