总结

• 指数型：state[]
• 排列型：state[] used[]
• 组合型：state[] startIndex（startIndex标记从输入数组的哪一个位置开始遍历）

指数型枚举

每个数字要么选要么不选

方法1：数组

dfs思考递归搜索树，用state[]数组记录状态

import java.util.*;
public class Main{static boolean[] state; //记录选择状态 为true表示选择static int n;public static void main(String[] args){Scanner sc = new Scanner(System.in);n = sc.nextInt();state = new boolean[n + 1];dfs(1);}public static void dfs(int index){if(index > n){//输出for(int i = 1; i <= n; i++){if(state[i]) System.out.print(i + " ");}System.out.println();return;}state[index] = true;dfs(index + 1);state[index] = false;dfs(index + 1);}
}

方法2：List

import java.util.*;
public class Main{static LinkedList path;static List> res;static int n;public static void main(String[] args){Scanner sc = new Scanner(System.in);n = sc.nextInt();path = new LinkedList<>();res = new ArrayList<>();dfs(1);for(List path : res){for(int i : path) System.out.print(i + " ");System.out.println();}}public static void dfs(int index){if(index > n){//输出res.add(new ArrayList<>(path));return;}path.add(index);dfs(index + 1);path.removeLast();dfs(index + 1);}
}

例题：lc784. 字母大小写全排列

https://leetcode.cn/problems/letter-case-permutation/description/

tips1：

• 查看ASCII表可以发现ASCII在 65-90 之间是大写字母，97-122 是小写字母，即大小写相差32，可以使用位运算进行快捷转换

• 位运算进行字母大小写转换arr[index] ^= 32;

tips2：

• 使用Character.isDigit(arr[index])快捷判断是否是数字

代码

class Solution {List res;int len;public List letterCasePermutation(String s) {res = new ArrayList<>();len = s.length();dfs(s.toCharArray(),0);return res;}public void dfs(char[] arr, int index){while(index < len && Character.isDigit(arr[index])) index++;//最底端if(index == len){res.add(new String(arr));return;}//先变大小写arr[index] ^= 32;dfs(arr,index + 1);//变回来arr[index] ^= 32;dfs(arr,index + 1);}
}

遍历过程

[A1B2,A1b2,a1b2,a1B2]

排列型枚举

排列型

https://leetcode.cn/problems/permutations/description/

方法1：数组

两个数组记录状态

state[]数组记录每个位置的状态

used[]数组记录数值是否用过

import java.util.*;public class Main{static int n;static int[] state; //记录路径static boolean[] used; //记录当前数字是否用过public static void main(String[] args){Scanner sc = new Scanner(System.in);n = sc.nextInt();used = new boolean[n + 1];state = new int[n + 1];dfs(1);//因为答案要求从1开始}public static void dfs(int index){if(index > n){for(int i = 1; i <= n; i++){System.out.print(state[i] + " ");}System.out.println();return;}for(int i = 1; i <= n; i++){if(used[i]) continue;used[i] = true; //记录已经使用过state[index] = i; //记录路径dfs(index + 1);used[i] = false;}}
}

方法2：List

import java.util.*;public class Main{static int n;static LinkedList path;static List> res;static boolean[] used; //记录当前数字是否用过public static void main(String[] args){Scanner sc = new Scanner(System.in);n = sc.nextInt();used = new boolean[n + 1];path = new LinkedList<>();res = new ArrayList<>();// state = new int[n + 1];dfs(1);//因为答案要求从1开始for(List path : res){for(int i : path) System.out.print(i + " ");System.out.println();}}public static void dfs(int index){if(index > n){res.add(new ArrayList<>(path));return;}for(int i = 1; i <= n; i++){if(used[i]) continue;used[i] = true; //记录已经使用过path.add(i);dfs(index + 1);used[i] = false;path.removeLast();}}
}

变形：数组中有重复元素 需要返回结果不能重复

• 剑指Offer 38. 字符串的排列

https://leetcode.cn/problems/zi-fu-chuan-de-pai-lie-lcof/description/

注意点：排序以及加入树层去重

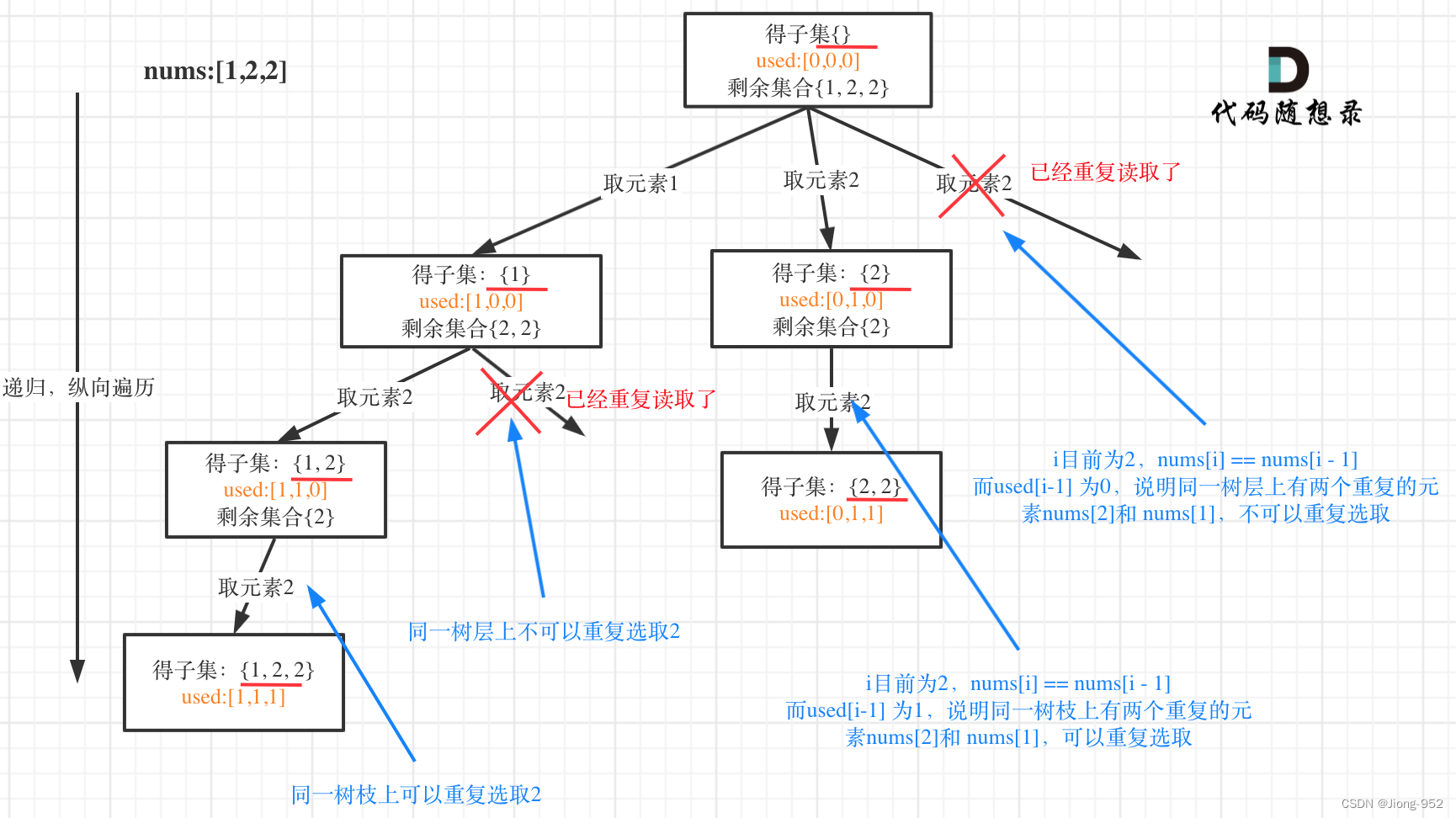
Arrays.sort(arr);

if(i - 1 >= 0 && arr[i - 1] == arr[i] && used[i-1] == false) continue;

class Solution {//全排列问题char[] arr;StringBuilder path = new StringBuilder();List res = new ArrayList<>();boolean[] used;public String[] permutation(String s) {arr = s.toCharArray();Arrays.sort(arr);used = new boolean[arr.length];dfs(0);String[] ans = new String[res.size()];for(int i = 0; i < res.size(); i++){ans[i] = res.get(i);}return ans;}public void dfs(int index){if(index == arr.length){res.add(path.toString());return;}for(int i = 0; i < arr.length; i++){//加入同一层去重 如果前面已经用过则不再使用防止重复if(i - 1 >= 0 && arr[i - 1] == arr[i] && used[i-1] == false) continue;if(!used[i]){used[i] = true;path.append(arr[i]);dfs(index + 1);path.deleteCharAt(path.length() - 1);used[i] = false;}}}
}

lc47. 全排列 II

https://leetcode.cn/problems/permutations-ii/description/

class Solution {List> res;LinkedList path;boolean[] used;int[] nums;public List> permuteUnique(int[] nums) {//去重的核心是排序res = new ArrayList<>();path = new LinkedList<>();used = new boolean[nums.length];Arrays.sort(nums);this.nums = nums;backtracking();return res;}public void backtracking(){if(path.size() == nums.length){res.add(new ArrayList<>(path));return;}for(int i = 0; i < nums.length; i++){//nums[i] == nums[i - 1] && used[i - 1] == false表明当前和上一个值一样，但是上一个已经用过if(i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;if(used[i] == false){used[i] = true;path.add(nums[i]);backtracking();used[i] = false;path.removeLast();}}}
}

组合型枚举

https://leetcode.cn/problems/combinations/description/

方法1：数组

state[]数组记录每个位置的状态，即路径

startIndex记录遍历位置

n相当于树的宽度，m相当于树的深度

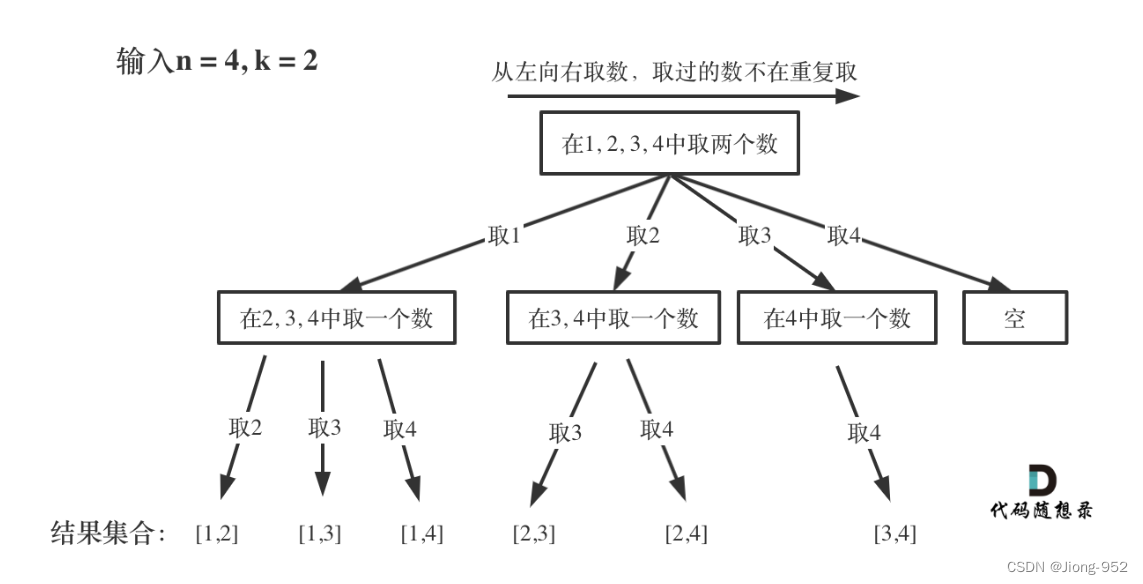
import java.util.*;
public class Main{static int[] state; //记录路径，m个位置都放的是什么数static int n;static int m;public static void main(String[] args){Scanner sc = new Scanner(System.in);n = sc.nextInt();m = sc.nextInt();state = new int[m]; dfs(0,1);}public static void dfs(int index,int startIndex){// 剪枝//已经不足m个if(index + n - startIndex  + 1 < m) return;if(index == m){//叶子结点for(int i = 0; i < m; i++) System.out.print(state[i] + " ");System.out.println();return;}for(int i = startIndex; i <= n; i++){state[index] = i;dfs(index + 1, i + 1);state[index] = 0;}}
}

方法2：List

import java.util.*;
public class Main{// static int[] state; //记录路径，m个位置都放的是什么数static int n;static int m;static LinkedList path;static List> res;public static void main(String[] args){Scanner sc = new Scanner(System.in);n = sc.nextInt();m = sc.nextInt();path = new LinkedList<>();res = new ArrayList<>();dfs(0,1);for(List path : res){for(int i : path) System.out.print(i + " ");System.out.println();}}public static void dfs(int index,int startIndex){// 剪枝if(index + n - startIndex  + 1 < m) return;if(index == m){//叶子结点res.add(new ArrayList<>(path));return;}for(int i = startIndex; i <= n; i++){path.add(i);   dfs(index + 1, i + 1);path.removeLast();}}
}

变形

https://leetcode.cn/problems/combination-sum-iii/description/

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

• 只使用数字1到9
• 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示:

• 2 <= k <= 9
• 1 <= n <= 60

code

class Solution {List> res = new ArrayList<>();LinkedList path = new LinkedList<>();public List> combinationSum3(int k, int n) {dfs(k,n,1,0);return res;}public void dfs(int k, int target, int startIndex, int sum){// 剪枝if(sum > target) return;if(path.size() + 9 - startIndex + 1 < k) return;// 到底if(path.size() == k && sum == target){res.add(new ArrayList<>(path));return;}for(int i = startIndex; i <= 9; i++){path.add(i);dfs(k,target,i+1,sum+i);path.removeLast();}}
}

带分数

方法1:

暴力全排列+枚举

import java.util.*;
public class Main{static int target; //目标等式的左边static int[] nums;  //目标等式的右边static boolean[] used; //记录用过的数字static int cnt; //记录结果数static int N = 10;public static void main(String[] args){Scanner sc = new Scanner(System.in);target = sc.nextInt();nums = new int[N];used = new boolean[N];dfs(0);System.out.println(cnt);}//根据数组左右返回数值public static int cal(int l, int r){int res = 0;for(int i = l; i <= r; i++){res = res * 10 + nums[i];}return res;}public static void dfs(int index){if(index == 9){//新的全排列//开始枚举a b cfor(int i = 0; i < 7; i++){for(int j = i + 1; j < 8; j++){int a = cal(0,i);int b = cal(i + 1, j);int c = cal(j + 1, 8);//去掉0if(a == 0 || b ==0 || c == 0) continue;//判断是符合if(c * target == c * a + b) cnt++;}}return;}//继续搜索for(int i = 1; i <= 9; i++){if(!used[i]){used[i] = true;nums[index] = i;dfs(index + 1);used[i] = false;}}}
}

方法2：

剪枝优化，暴力枚举a ,c b自动得出，判断是否满足

import java.util.*;
public class Main{static int target;static boolean[] used;static int N = 10;static int cnt;public static void main(String[] args){Scanner sc = new Scanner(System.in);target = sc.nextInt();used = new boolean[N];dfs_a(0,0);System.out.println(cnt);}//index表示当前遍历到第几位//a表示当前a的值public static void dfs_a(int index, int a){if(index == 8 || a >= target) return;if(a > 0) dfs_c(index, a , 0);for(int i = 1; i <= 9; i++){if(!used[i]){used[i] = true;dfs_a(index + 1, a * 10 + i);used[i] = false;}}}public static void dfs_c(int index, int a, int c){if(index == 9) return;if(c > 0 && check(a,c)) cnt++;for(int i = 1; i <= 9; i++){if(!used[i]){used[i] = true;dfs_c(index + 1, a, c * 10 + i);used[i] = false;}}}//判断当前的a c是否符合条件public static boolean check(int a, int c){int b = (target - a) * c;if(a == 0 || b == 0 || c == 0) return false;boolean[] backup = used.clone();//先判断b中的数字是否有了，没有就标记为truewhile(b > 0){int x = b % 10;b /= 10;if(x == 0 | backup[x]) return false;backup[x] = true;}//判断used是否全部都用过了for(int i = 1; i <= 9; i++){if(!backup[i]) return false;}return true;}
}

array.clone()可以用于复制数组

• array：要复制的数组
• 方法返回一个copy数组