二进制哈希码快速搜索:Multi-Index Hashing
前言
如果你对这篇文章感兴趣,可以点击「【访客必读 - 指引页】一文囊括主页内所有高质量博客」,查看完整博客分类与对应链接。
哈希方法通常包含两个部分:
- 【编码】将元素通过「data-dependent」或「data-independent」的方式映射为二进制,并通过比较二进制码的汉明距离 (hamming distance) 来搜索相似元素;
- 【搜索】由于二进制码往往比较长(例如 64, 128, 256 bits),采用直接映射的方式,通常找不到任何元素,因此通常考虑找汉明距离小于 rrr 的元素,即二进制编码最多只有 rrr 个位置不同。
下文主要介绍 [TPAMI13 - Mohammad Norouzi] 中提出的「在汉明空间中,使用 Multi-index Hashing 精确快速搜索」的方法。
Multi-Index Hashing
首先介绍一下我们所关心的问题:
- 有 nnn 个元素,每个元素对应 qqq 位的二进制码;
- 给定一个查询元素,如何快速在 nnn 个元素中,找到与查询元素汉明距离小于等于 rrr 的元素。
如果直接搜索,则需要检查的不同的哈希桶 (hash buckets) 个数为:
L(q,r)=∑z=0r(qz).L(q,r)=\sum_{z=0}^r\left(\begin{array}{l} q \\ z \end{array}\right). L(q,r)=z=0∑r(qz).
这显然是不可接受的。因此为了加速上述过程,我们将每个包含 qqq 位的哈希码 h\mathbf{h}h 连续切分为了 mmm 个不相交的子串,h(1),...,h(m)\mathbf{h}^{(1)},...,\mathbf{h}^{(m)}h(1),...,h(m),每个子串包含 q/mq/mq/m 位。
若两个哈希码 h\mathbf{h}h 和 g\mathbf{g}g 最多相差 rrr 位,则在 mmm 个子串中,至少存在一个子串,两个哈希码相差的位数不超过 ⌊r/m⌋\lfloor r / m\rfloor⌊r/m⌋,即对应下述结果:

上述结果即说明,为了找到与 h\mathbf{h}h 相差位数小于等于 rrr 的元素,只需分别在 mmm 个子串中寻找汉明距离小于等于 r′r'r′ 的元素,然后再一一检查小于 r′r'r′ 的元素是否满足小于 rrr 的要求,整体时间开销得到下降。
当然,上述结果还可以进一步提升,即:
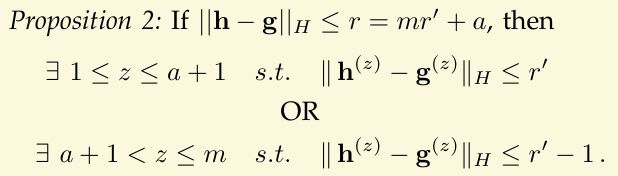
具体证明思路是:假设第一个结论不成立,则 h\mathbf{h}h 和 g\mathbf{g}g 在前 a+1a+1a+1 个子串中至少一共有 (a+1)(r′+1)(a+1)(r'+1)(a+1)(r′+1) 位不同,即在剩下的 m−(a+1)m-(a+1)m−(a+1) 个子串中,只需找有 r−(a+1)(r′+1)r-(a+1)(r'+1)r−(a+1)(r′+1) 位不同的元素。此时运用「Proposition 1」,即可得到:
⌊r−(a+1)(r′+1)m−(a+1)⌋=⌊mr′+a−(a+1)r′−(a+1)m−(a+1)⌋=⌊r′−1m−(a+1)⌋=r′−1\begin{aligned} \left\lfloor\frac{r-(a+1)\left(r^{\prime}+1\right)}{m-(a+1)}\right\rfloor & =\left\lfloor\frac{m r^{\prime}+a-(a+1) r^{\prime}-(a+1)}{m-(a+1)}\right\rfloor \\ & =\left\lfloor r^{\prime}-\frac{1}{m-(a+1)}\right\rfloor \\ & =r^{\prime}-1 \end{aligned} ⌊m−(a+1)r−(a+1)(r′+1)⌋=⌊m−(a+1)mr′+a−(a+1)r′−(a+1)⌋=⌊r′−m−(a+1)1⌋=r′−1
因此若第一个结论不成立,第二个结论必定成立。由此可知,为找到与 h\mathbf{h}h 相差位数小于等于 rrr 的元素,只需先在前 a+1a+1a+1 个子串中寻找距离小于等于 r′r'r′ 的元素,再在第 a+1a+1a+1 到第 mmm 个子串中寻找距离小于等于 r′−1r'-1r′−1 的元素即可,整体时间开销进一步得到下降。具体算法如下:
令 s=q/ms=q/ms=q/m 为每个子串的长度,根据「Proposition 1」可知,上述算法需要检索哈希表的总次数为: 其中不等号由组合数公式得到(需满足 r≤q/2r\leq q/2r≤q/2)。除了查表外,时间开销还包括将查到的元素进行比对,由于元素在哈希表内的分布难以确定,因此假定 nnn 个元素均匀分布在大小为 2s2^s2s 的哈希表中,即总时间开销为: 另外,文中指出当 s=log2ns=\log_2 ns=log2n 时,查搜效果较好,因此将 s=log2ns=\log_2 ns=log2n 代入 cost(s)\operatorname{cost}(s)cost(s),得到: 当 r/q≤.11r/q\leq .11r/q≤.11 时,H(.11)<.5H(.11)<.5H(.11)<.5,运行时间复杂度为 O(qn/log2n)O(q\sqrt{n}/\log_2 n)O(qn/log2n);当 r/q≤.06r/q\leq .06r/q≤.06 时,时间复杂度变为 O(qn3/log2n)O\left(q \sqrt[3]{n} / \log _2 n\right)O(q3n/log2n),即与 nnn 的关系为 sub-linear。 很多时候我们并不想找汉明距离小于等于 rrr 的元素,而是想找汉明距离最近的 kkk 个元素,但对于不同的查询元素,对于固定的 kkk,需要的 rrr 相差很大,如下图所示: 因此对于 k-NN\text{k-NN}k-NN 问题,我们可以将 rrr 从 000 向上遍历,直至找到 kkk 个元素为止,具体算法如下:
对于「Proposition 2」,有一个特殊情况,即当 r
性能分析
lookups(s)=qs∑z=0⌊sr/q⌋(sz)≤qs2H(r/q)s,\operatorname{lookups}(s)=\frac{q}{s} \sum_{z=0}^{\lfloor s r / q\rfloor}\left(\begin{array}{l} s \\ z \end{array}\right) \leq \frac{q}{s} 2^{H(r / q) s}, lookups(s)=sqz=0∑⌊sr/q⌋(sz)≤sq2H(r/q)s,
cost(s)=(1+n2s)qs∑z=0⌊sr/q⌋(sz),≤(1+n2s)qs2H(r/q)s.\begin{aligned} \operatorname{cost}(s) & =\left(1+\frac{n}{2^s}\right) \frac{q}{s} \sum_{z=0}^{\lfloor s r / q\rfloor}\left(\begin{array}{l} s \\ z \end{array}\right), \\ & \leq\left(1+\frac{n}{2^s}\right) \frac{q}{s} 2^{H(r / q) s} . \end{aligned} cost(s)=(1+2sn)sqz=0∑⌊sr/q⌋(sz),≤(1+2sn)sq2H(r/q)s.
cost(log2n)≤2qlog2nnH(r/q).\operatorname{cost}\left(\log _2 n\right) \leq 2 \frac{q}{\log _2 n} n^{H(r / q)}. cost(log2n)≤2log2nqnH(r/q).
K 近邻搜索
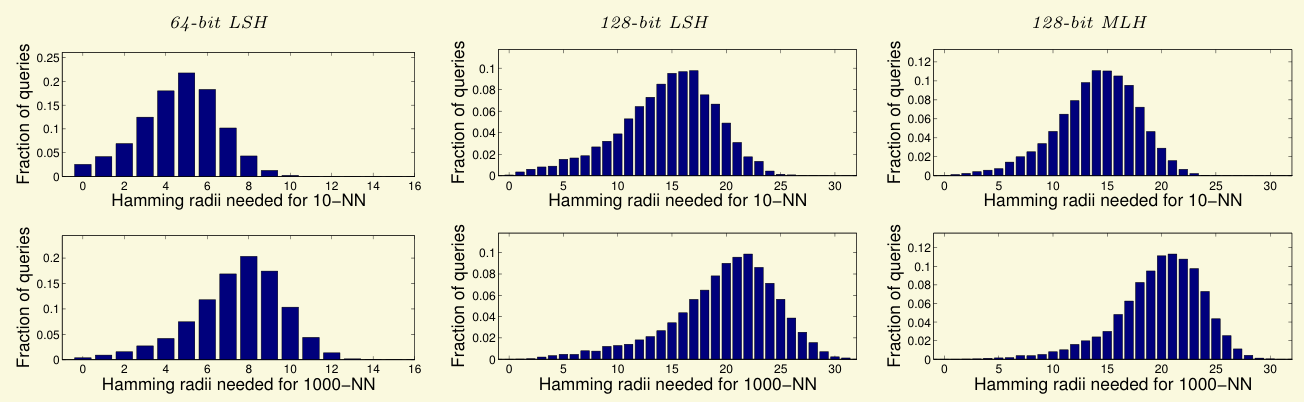
对于相同的 k-NN\text{k-NN}k-NN 问题,不同查询元素所需要的汉明距离 rrr 也不相同。
参考资料