摘要

剑指 Offer 60. n个骰子的点数

一、暴力方法

此方法超时，但为便于理解动态规划解析，建议先理解此方法。

• 每个骰子摇到1至6的概率相等，都为1/6​ 。
• 将每个骰子的点数看作独立情况，共有6^n点数组合。例如 n=2时的点数组合为：(1,1),(1,2),⋯,(2,1),(2,2),⋯,(6,1),⋯,(6,6)。
• n 个骰子点数和的范围为 [n,6n]，数量为6n−n+1=5n+1种。

暴力统计： 每个「点数组合」都对应一个「点数和」，考虑遍历所有点数组合，统计每个点数和的出现次数，最后除以点数组合的总数（即除以 6n ），即可得到每个点数和的出现概率。如下图所示，为输入n=2时，点数组合、点数和、各点数概率的计算过程。

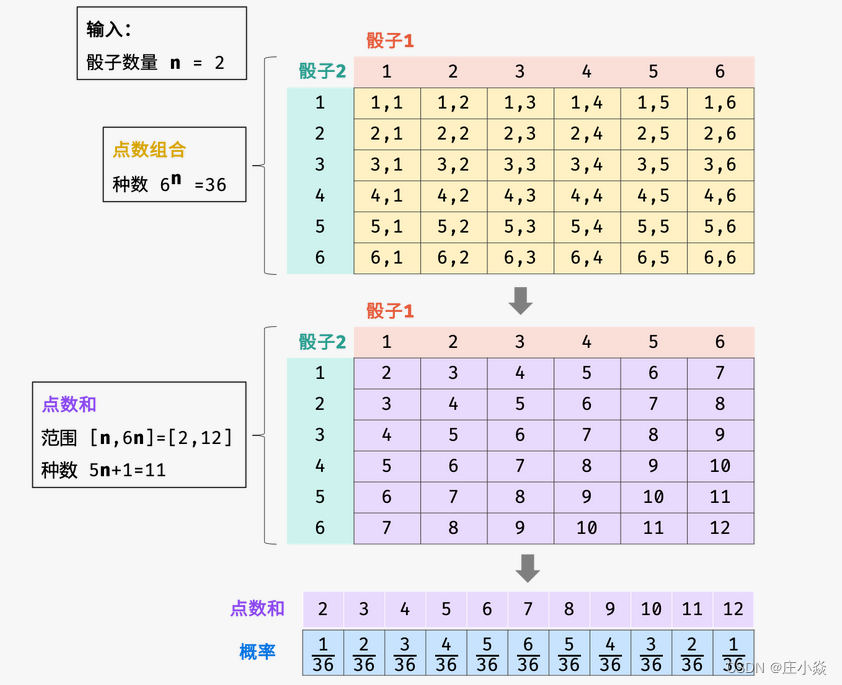
暴力法需要遍历所有点数组合，因此时间复杂度为 O(6^n) ，观察本题输入取值范围 1≤n≤11，可知此复杂度是无法接受的。

二、动态规划方法

设输入n个骰子的解即概率列表为 f(n)，其中「点数和」x的概率为 f(n,x)。

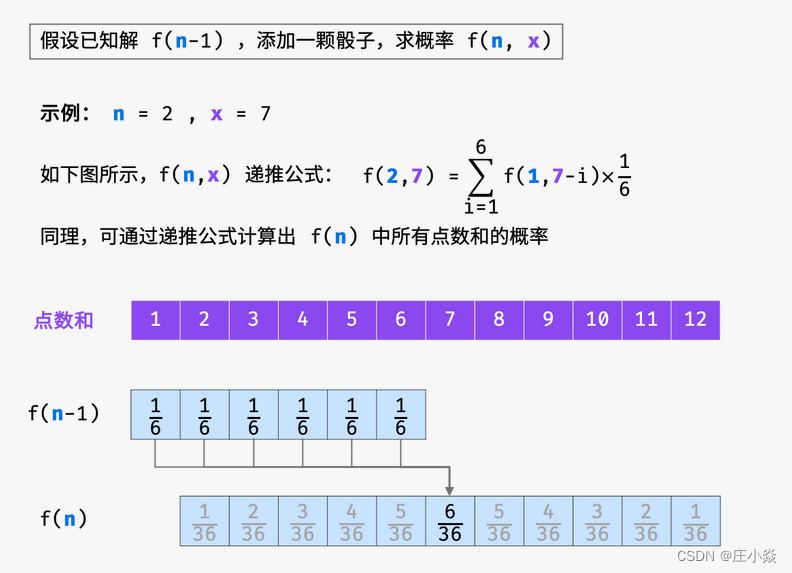
假设已知n−1个骰子的解 f(n−1)，此时添加一枚骰子，求n个骰子的点数和为x 的概率f(n,x) 。

当添加骰子的点数为1时，前n−1个骰子的点数和应为x−1 ，方可组成点数和x ；同理，当此骰子为 2时，前n−1    个骰子应为 x−2 ；以此类推，直至此骰子点数为6 。将这6种情况的概率相加，即可得到概率 f(n,x) 。递推公式如下所示：

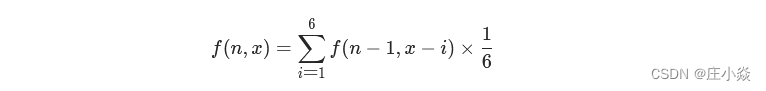
根据以上分析，得知通过子问题的解f(n−1) 可递推计算出 f(n)，而输入一个骰子的解 f(1)已知，因此可通过解 f(1)依次递推出任意解 f(n) 。

观察发现，以上递推公式虽然可行，但 f(n−1,x−i)中的 x−i会有越界问题。例如，若希望递推计算 f(2,2) ，由于一个骰子的点数和范围为 [1,6]，因此只应求和 f(1,1)，即 f(1,0) , f(1,−1) , ... , f(1,−4) 皆无意义。此越界问题导致代码编写的难度提升。

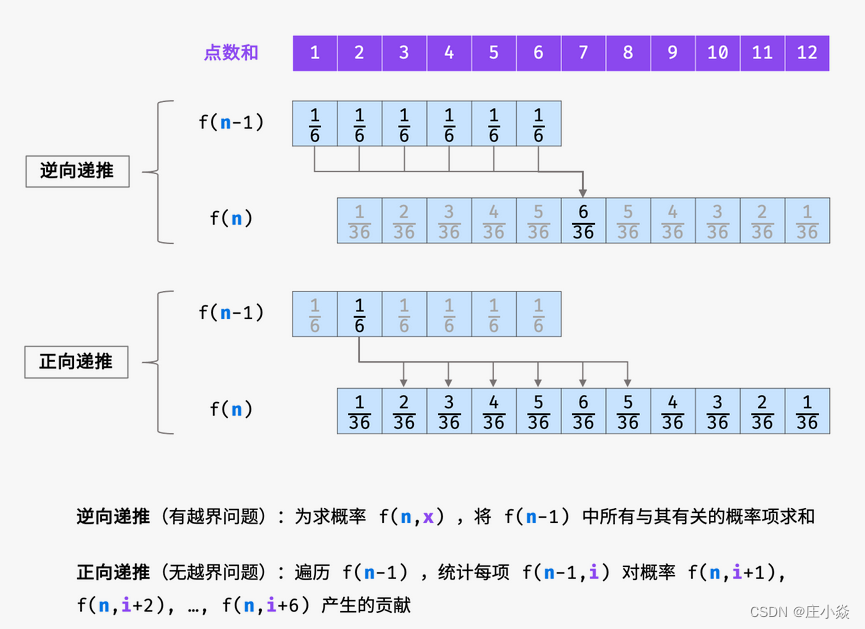
具体来看，由于新增骰子的点数只可能为1至6 ，因此概率 f(n−1,x)仅与 f(n,x+1) , f(n,x+2), ... , f(n,x+6)相关。因而，遍历 f(n−1)中各点数和的概率，并将其相加至f(n)中所有相关项，即可完成 f(n−1)至 f(n)的递推。

    public double[] dicesProbability2(int n) {// 表示的i个骰子的时候的等于j的和多少种情况 f(i,j)=f(i-1,j-1)+f(i-1,j-2)+……f(i-1,j-6)int[][] dp = new int[n + 1][6 * n + 1];// f(i,1)=1 f(1,2)=1 …… f(1,6)=1for (int i = 1; i <= 6; i++) {dp[1][i] = 1;}// i表示的i个骰子for (int i = 2; i <= n; i++) {// j 表示的和为j的情况for (int j = i; j <= 6 * i; j++) {// f(i,j)=f(i-1,j-1)+f(i-1,j-2)+……f(i-1,j-6)for (int k = 1; k <= 6; k++) {if (j < k) {break;}dp[i][j] += dp[i - 1][j - k];}}}double[] res=new double[5*n+1];int index=0;double sum= Math.pow(6,n);// n 表示的n骰子的情况for (int i=n;i<=6*n;i++){res[index++]=dp[n][i]/sum;}return res;}

复杂度分析：

• 时间复杂度 O(n^2) ： 状态转移循环 n−1轮；每轮中，当 i=2,3,...,n时，对应循环数量分别为 6×6,11×6,...,[5(n−1)+1]×6；总体复杂度为O((n−1)×6+[5(n−1)+1]2×6)，即等价于O(n^2) 。
• 空间复杂度 O(n) ： 状态转移过程中，辅助数组 tmp 最大长度为6(n−1)−[(n−1)−1]=5n−4，因此使用 O(5n−4)=O(n)大小的额外空间。

博文参考

《leetcode》