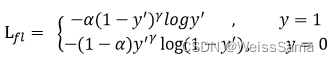2023 03 11 写在前面：
这里是为了面试的，所以都只写了结论，有些问题可以延伸出很多相关问题，比如从BN可以到GN，从Pooling可以到ROI Pooling，GAP，UnPooling…,一个问题可以延伸出太多问题，所以尽量给出问题延伸出的相关问题的链接。

合适大小batch size的意义

在合理范围内增大batch size的优点：
优点1 内存利用率提高，大矩阵乘法的并行优化效率提高
优点2 跑完一个epoch时间减少
优点3 在一个范围内，batch size越大，其确定的梯度下降方向越准，引起的训练震荡越小盲目增大batch size的缺点
1.内存撑不住
2.batch size增大到一定程度，其确定的梯度下降方向基本不变了，陷入局部最优解

Epoch 和 Iteration

Epoch指的是全部训练数据再模型上跑完一轮
Iteration指的是一个Batch在模型上跑完一轮

介绍Batch Normalization和Group Normalization，以及优缺点。

BN的优点是网上谈过无数次的问题，不过我还是写了一篇博客具体介绍。博客地址
再说优缺点
首先关于BN，BN虽然很伟大，但是并不是没有缺点的，比如当我们的模型非常大的时候我们只能设置比较小的Batch Size，毕竟内存就那么多。
而GN，在每个特征图BxHxWxC中，它将channel分成多个组，在每组内计算均值和方差，GN的计算与BatchSize无关，在Batch SIze小的时候带来的精度远超BN，而适当Batch Size的时候，BN和GN效果相当。

当然还有Weight Normalization，Instanc Normalization，Layer Normalization。。

介绍一下集中Pooling方法，及其作用

average pooling，max pooling， global average pooling(GAP)。

average pooling也可以叫local average pooling，GAP是average pooling的特例，
它提出来的作用是取代参数巨多容易过拟合的全卷积层。举例有一个feature map，假设batch为1，channel是10，1x6x6x10的feature map，
gap通过对每一个channel的6x6的map进行49个值加和平均，输出是 1x1x1x10=1x10维的向量。average pooling的输出则是根据pool_size, strides, padding，
比如string=2，计算出来的feature map就是1x3x3x10。gap只是average pooling的一个特例。它的作用可以参考下一个问题

最后一个是maxpooling的逆向操作，MaxUnpooing。也就是根据记录的max pooling时候的max index来返现生成原来的特征图。

Global average pooling (GAP)的作用

GAP一般用来替代全卷积，放在softmax分类之前，
GAP用简单的平均方法建立起了feature map和category之间的联系。以分类问题为例，最终的 channel个数一般等于类别个数，
就是每个类别仅仅对应一个feature map，每个feature map内部求平均，
10个feature map就变成了一个10维向量，然后输入到softmax中。全连接层过于依赖dropout来避免过拟合，而global average pooling可以看做是一种结构化正则，
即对多个feature map的空间平均（spatial average），能够适用输入的许多空间变化（翻转、旋转，平移，尺度，等）。同时它不引入参数，缓解过拟合。

CNN的平移不变性？

结论在最后

解释一下什么是CNN的平移不变性。
简单来说，平移不变性（translation invariant）指的是CNN对于同一张图及其平移后的版本，都能输出同样的结果。
这对于图像分类（image classification）问题来说肯定是最理想的，
因为对于一个物体的平移并不应该改变它的类别。而对于其它问题，比如物体检测（detection）、物体分割（segmentation）来说，
这个性质则不应该有，原因是当输入发生平移时，输出也应该相应地进行平移。
这种性质又称为平移等价性（translation equivalence）。
这两个概念是比较混淆的，但确实是两个不同的东西（敲黑板）。先来分析单层的情况。
(1) 卷积层：在信号处理中，卷积（以及相关）的性质包含了平移等价性（translation equivalence）。
对于共享权值的卷积层来说，只在平移量为stride的整数倍时平移等价性才严格成立。
而仅仅在卷积核比较均匀而且输入也有很多均匀区域的时候才有比较弱的（translation invariant），因为此时微小的移动对于输出改变比较少。(2) 池化层：普通池化层中，均值池化average pooling其实也可以理解成是一种平均滤波卷积，
它并没有非线性，因此性质也同上面分析的卷积层相同；最大值池化max pooling也类似，但取最大值的操作使其相对于均值带有更强的平移不变性。(3) 全局池化层global average pooling: 上一个问题解释了，gap将整个输入变成1x1大小的输出，忽略了特征的空间位置信息，当前面的输入具有平移等价性的时候具有比较强的平移不变性。(4) 全连接层：全连接层这两个性质都没有，因为没有在不同位置共享权值，特征在不同位置对于输出的贡献变化很大。参数的学习需要数据，由于数据中平移的分布一般都比较不均匀，引入平移的数据增强（augmentation）肯定是必要的。
那有人会问，为什么好像没看到有这个增强方式？
其实裁切（crop）就是一种平移的数据增强方式，因为不同裁切方式对应的patch之间的变换就是平移。
而且这种方式相比于平移更加自然，没有周围的黑边padding，因此更加常用。

所以在使用全连接层的时候整个CNN的结构一般不具有平移不变性。
就算用了全局池化层gap，由于前面叠加的多层卷积层的累计效应，最后的平移不变性也很弱，只有当位移是整个网络的降采样倍数的整数倍才存在。
CNN的平移不变性主要是通过数据学习来的，结构只能带来非常弱的平移不变性，
而学习又依赖于数据增强中的裁切，裁切相当于一种更好的图像平移。

参考 https://www.cvmart.net/community/detail/240
论文 http://proceedings.mlr.press/v97/zhang19a.html

Pooling的作用

首先pooling不引入额外参数，降低计算消耗，这是一个优点，也是出发点。average pooling，可以看成是一个kernel参数为常数的卷积，平均滤波卷积
所以我们只需要知道卷积的作用是什么就知道了，
不就是参数共享，提取特征，对于average这种操作提取的主要还是背景信息，因为背景远远多于目标
步长大于1的时候所有层都有的特点，增大感受野，降采样，去除冗余信息。max pooling
我们说的pooling的作用，其实一般指的是max pooling的作用
首先，max pooling引入了非线性机制，而非线性会缓建过拟合。
然后，max pooling的步长都大于1，一般是2，它提取的信息是纹理特征信息，也可以说是物体信息而不是背景
最后，像上一个问题中描述的，max pooling对选择，平移，尺度变换等有较强的不变性。global average pooling的作用，直接看上上个问题。adaptive pooling，自适应池化，引入学习参数，融合avgpooling和maxpooling，更好地提取特征，可以涨点。

介绍几种CV中数据增强data augmentation方法

我这里先以yolov4&v5中用到的数据增强方法进行介绍。
random crop：可保留主要特征，裁剪掉背景噪声
random erasing：随机选择一个区域，然后采用随机值进行覆盖，模拟遮挡场景
mixup：两张图按0.5比例叠加，增加样本数量，丰富了目标背景，提高模型的泛化能力
cutout：只用正方形填充，填充值只有0或其他纯色填充（作者发现区域的大小比形状更重要）
cutmix：cutout和mixup结合，将图片的一部分区域擦除并随机填充训练集中的其他数据区域像素值

mosaic：cutmix的升级版，cutmix是两张图片混搭，而masaic是四张图片混搭，具体地

1. 在一个空白幕布张随机选择一个拼接点xc，yc
2. 四张图片根据拼接点，分别经过尺度调整和比例缩放之后，放置在基准点的四周
3. 根据每张图的变换方式，同步的变换他妈的groung truth
4. 处理掉超过图片边际的像素
   这里给出一张超不清网图。。
   

YOLOV4相比于YoloV3有哪些改进

参考博客 地址
参考博客 地址

Weighted Residual Connection WRC

Cross Stage Partial DarkNet
CSPDarknet 我的博文

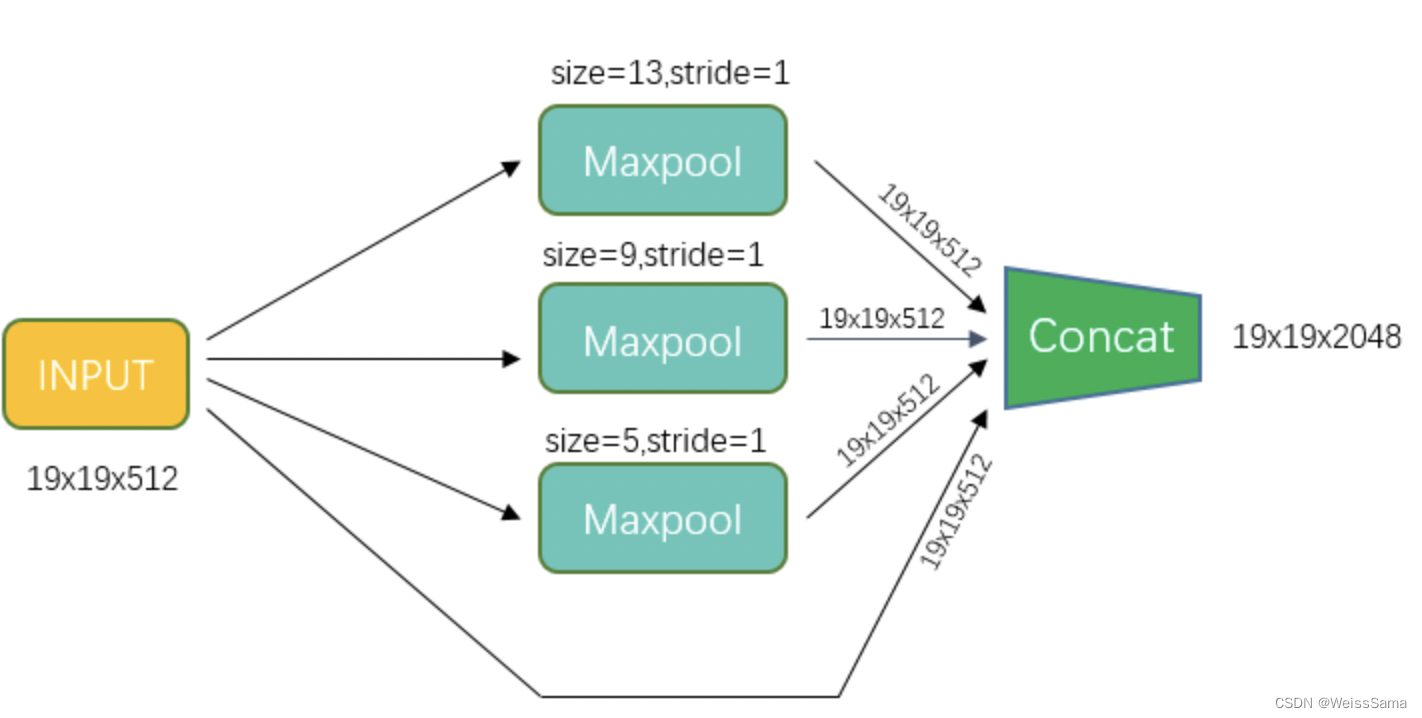
SPP
金字塔pooling，通不同的kernel size对input进行max pooling，所以每次移动都是一个
13x13 或者 9x9 或者5x5区域的最大值。这些最大值构成了最终的三个19x19x512 feature map

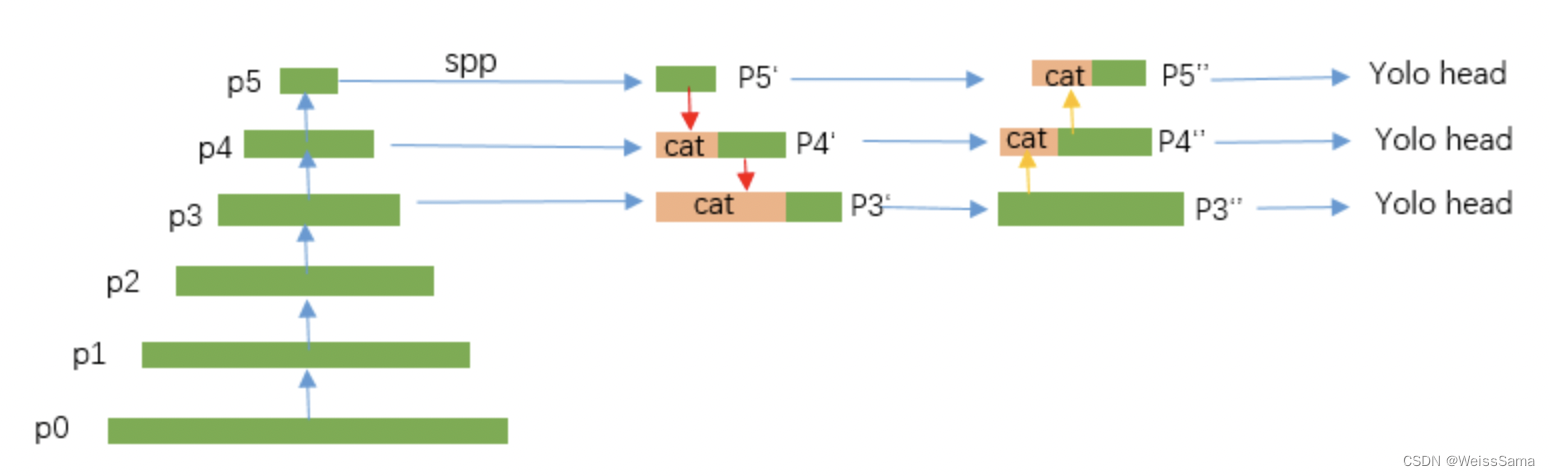
PAN
SPP为了PAN而使用的，图解可以看上述博客，PANet是加强版的FPN，不仅有FPN的自顶向下的特征融合，还加上了自底向上的特征融合，两者融合在一起来增加模型的表征能力。
下图是PAN，结构中包括了两次上采样和两次下采样。

Cross mini BN

Spatial Attention Module
参考我的文章地址

Mosaic data augmentation
见上一个问题

DropBlock Regularization

CIou Loss
见下一个问题

Smooth L1 Loss 和它的改进版本各种 IoU Loss

我们从L1 loss 开始看吧，L1 loss又被称为
L1范数损失
最小绝对偏差（LAD）
平均绝对值误差（MAE）
它的优点就是梯度稳定，缺点是在x=0的地方，梯度不存在。而L2 Loss被称为
L2范数损失
最小均方误差（LSE）
均方误差（MSE）
优点：各点都连续光滑，方便求导，具有较为稳定的解
缺点：不是特别的稳健，因为当函数的输入值距离真实值较远的时候，对应loss值很大在两侧，则使用梯度下降法求解的时候梯度很大，可能导致梯度爆炸。
一般在回归任务
或者数值特征不大（防止loss太大，继而引起梯度大，梯度爆炸）
或者问题维度不高（loss本身比较简单，高纬度的还是得要更复杂的loss支撑）

Smooth L1 Loss成名是在Faster Rcnn中作为预测位置损失。表达如下

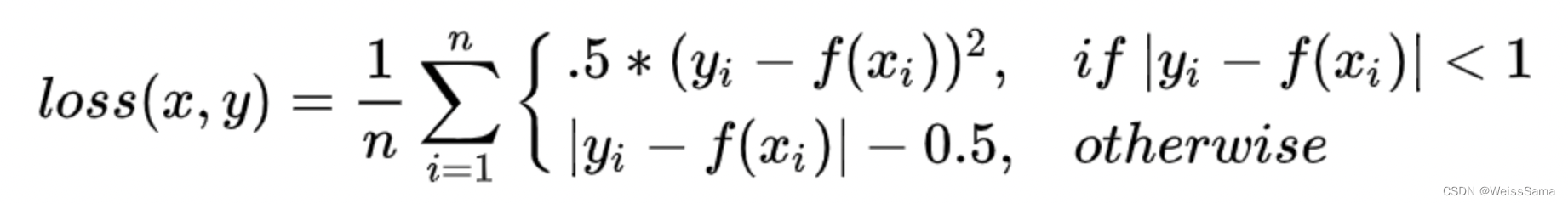
在预测值和真实值差别不大的时候，用的是L2 loss，此次梯度的差别也比较小，等于两者之差。而两者差别较大的时候，smooth l1 loss对那些离群的点不那么敏感，不会导致大规模的梯度变化。

介绍完了smooth l1 loss，再来说说它的进化版本，IoU loss系列。
回忆一下faster rcnn的思想，它投入到smooth l1 loss的并不是location的坐标
而是变换参数，包括平移变换参数和尺度变换参数，可以去复习一下 https://blog.csdn.net/zijin0802034/article/details/77685438上面的smooth l1 loss中，是独立的求出四点点的loss，然后相加得最终loss，但是其实这四点是互相关联的
我们应用引入一种loss，专门衡量位置损失，并且充分利用到几个参数之间有关联的特点
那用IoU不就好了
IoU越大代表预测框和真正框越接近，那么我们用 1-Iou = Iou_loss'
但是，IoU loss也不够好，
缺点1：IOU=0的时候，无法反应两个框距离的大小（重合度），此时loss=0，损失函数不可导，没有梯度回传，无法进行学习训练，IOU_Loss无法优化两个框不相交的情况。缺点2：即下图状态2和状态3的情况，当两个预测框大小相同，两个IOU也相同，IOU_Loss无法区分两者相交情况的不同。更直观的说，下面三个框，三种情况IoU都相等，但看得出来他们的重合度是不一样的，左边的图回归的效果好，右边差。

继续改进Iou loss，提出来了GIoU（Generalized Intersection over Union)
由于IoU是比值的概念，对目标物体的scale是不敏感的。
然而检测任务中的BBox的回归损失优化和IoU优化不是完全等价的，
而且 Ln 范数对物体的scale也比较敏感，IoU无法直接优化没有重叠的部分先计算两个框的最小外接矩形，假设面积是C，同时也可以求出交集I和并集B
最小外接矩形引入了尺度信息。
再计算出IoU，再计算最小外接矩形中不属于两个框的区域占最小外接矩形的比重=(C-B)/C，
这个(C-B)/C越小，说明两者交互程度越深。
最后用IoU减去这个比重得到GIoU=IoU - (C-B)/C 。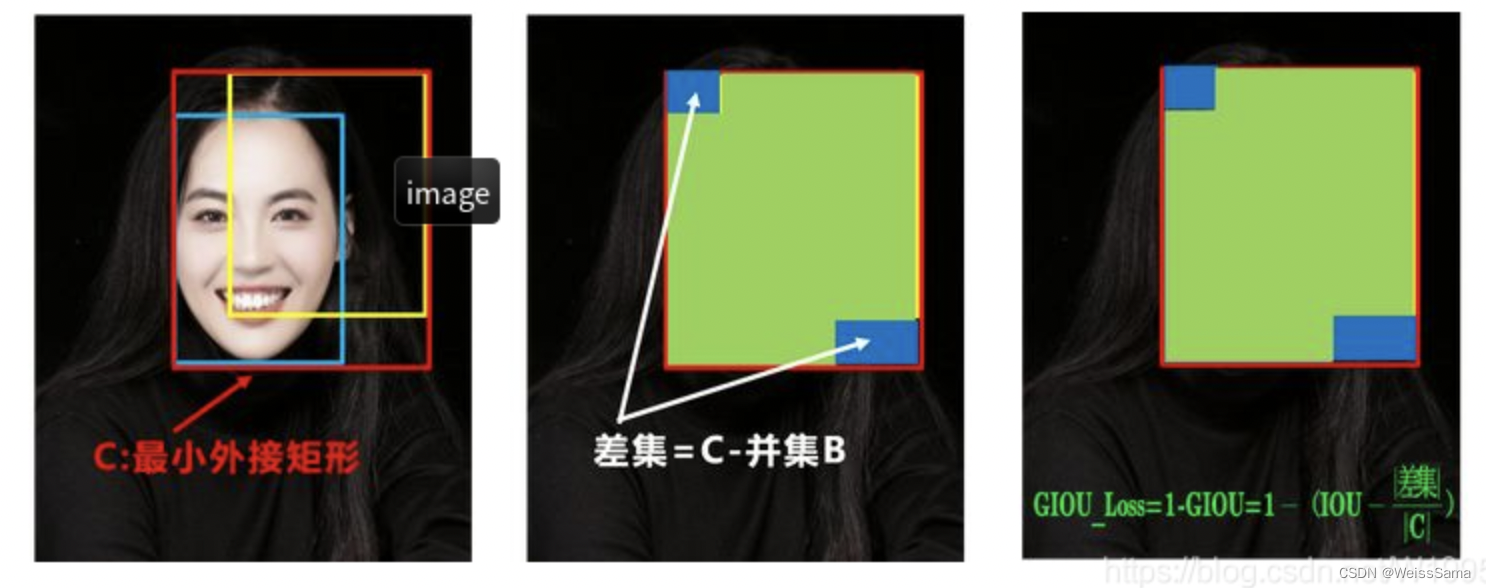

缺点，无法区分相对位置，下面三种情况下，GIOU值一样的，GIoU对于包含情况较差。

再引入一个Distance IoU，DIOU。
DIoU要比GIou更加符合目标框回归的机制，将目标与anchor之间的距离，重叠率（面积）以及尺度
都考虑进去，使得目标框回归变得更加稳定，不会像IoU和GIoU一样出现训练过程中发散等问题。当目标框包裹预测框的时候，直接度量2个框的距离，因此DIOU_Loss收敛的更快
其中，b , bgt 分别代表了预测框和真实框的中心点，且 ρ 代表的是计算两个中心点间的欧式距离。
c 代表的是能够同时包含预测框和真实框的最小外包矩形的对角线距离。DIoU优点：
1. GIoU loss类似，DIoU loss（ = 1-DIOU ）在与目标框不重叠时，仍然可以为边界框提供移动方向。
2. DIoU loss可以直接最小化两个目标框的距离，因此比GIoU loss收敛快得多。
3. 对于包含两个框在水平方向和垂直方向上这种情况，DIoU损失可以使回归非常快，而GIoU损失几乎退化为IoU损失
4. DIoU还可以替换普通的IoU评价策略，应用于NMS中，使得NMS得到的结果更加合理和有效。DIoU 缺点：
没有考虑到长宽比。下面三种请款预测框的中心点的位置都是一样的，因此按照DIOU_Loss的计算公式，三者的值都是相同的。

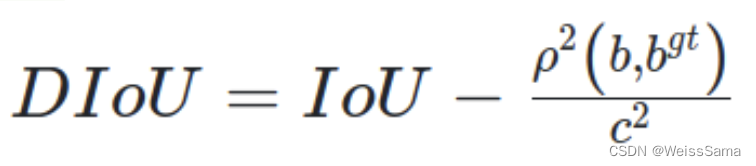
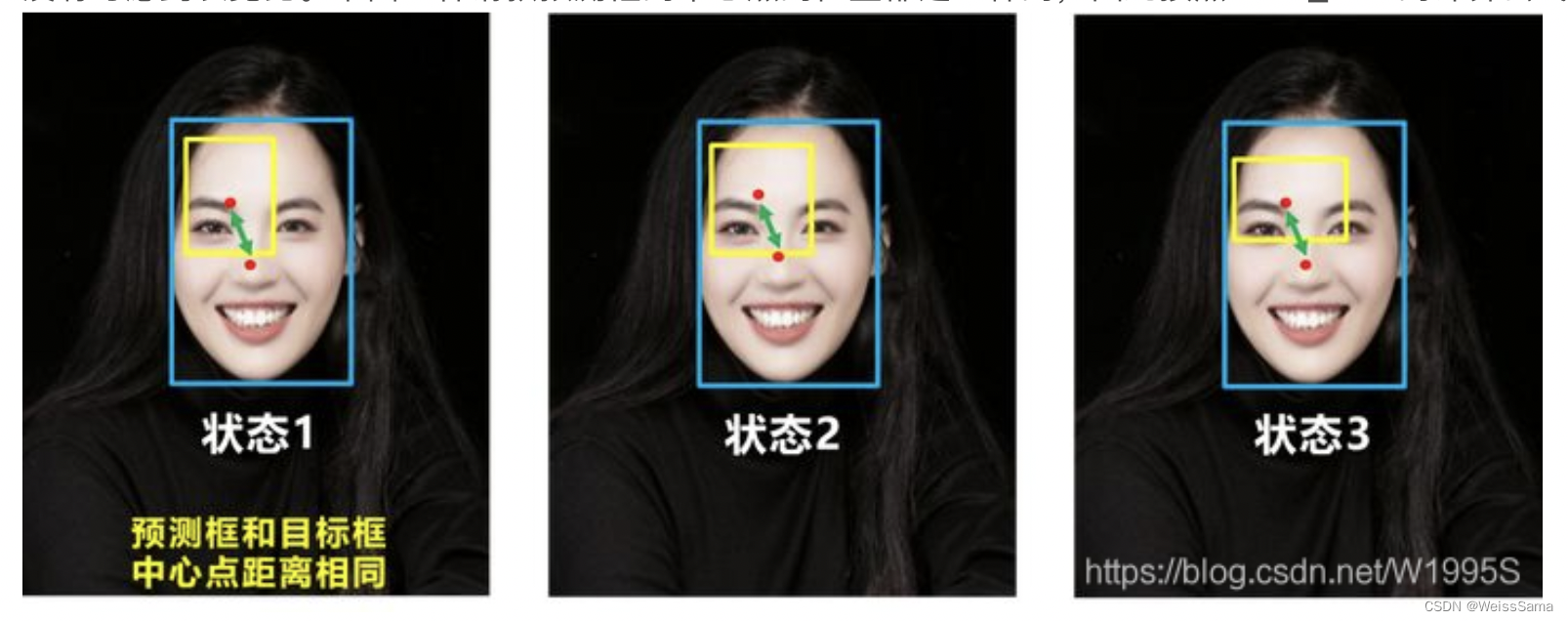
CIoU（Complete-IoU）在DIoU的基础上增加了一个长宽比的影响因子。
公式如下图一，其中$\alpha$ 是权重常数，v是用来衡量长宽比的相似性
v的定义如下图2

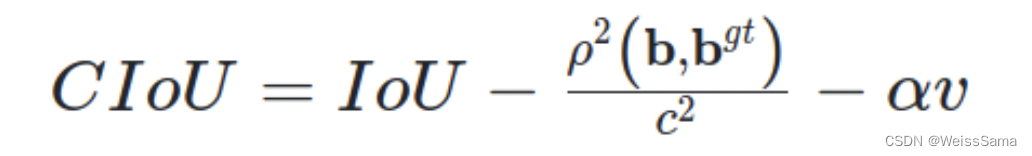
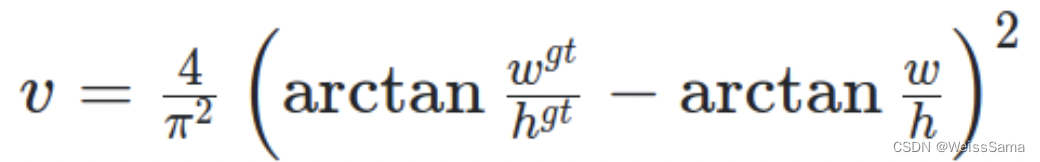
CIoU loss的梯度类似于DIoU loss，但还要考虑 v 的梯度。在长宽在 [0, 1] 的情况下， w2+h2w^{2}+h^{2}w2+h2通常会很小，会导致梯度爆炸，因此在 1w2+h2\frac{1}{{w^2}+{h^2}}w2+h21​ 实现时将替换成1。

Roi pooling和Roi align介绍区别，还有Roi warp

参考 图解 RoIPooling、RoIAlign 和 RoIWarp

RoI（Region of Interest） 是从原始图像中提取的区域。
我们不打算讲解如何提取这些区域，因为有很多方法可以做到。
我们现在唯一应该知道的是，有多个类似的长宽不同区域，最后都应该接受测试。feature map和原图之间有一个多次下采样造成的比例，一般是16或者32等等。
通过这个倍数我们可以找到roi 在feature map上的位置。其实这个过程中由于去整会造成一些精度损失 Quantization losses
RoIAlign它可以修复这个问题，但Roi pooling不能。

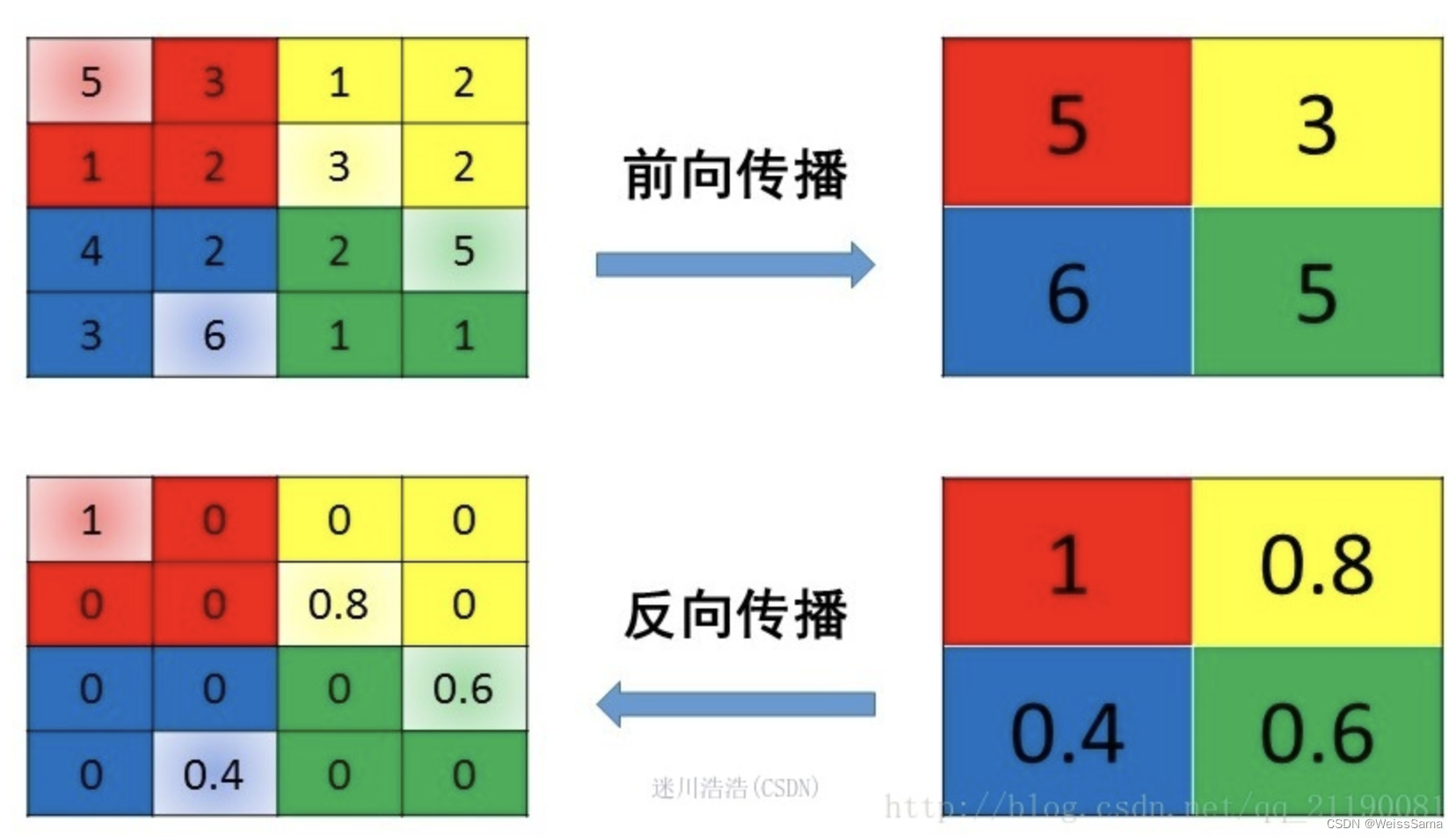
我们的目的是不管什么形状的Roi，经过我们的Roi pooling之后，得到的得到的结果都是一样的，假设我们需要的结果size是3x3，那么我们根据结果去反推pooling时候的面积。
我们看看这个过程，输入的feature map大小是4x6xchannel，roi pooling的结果是3x3xchannel，而4//3=1, 6//3=2；这意味着，我们做pooling的面积是1x2，stride默认是1.那么如下图。

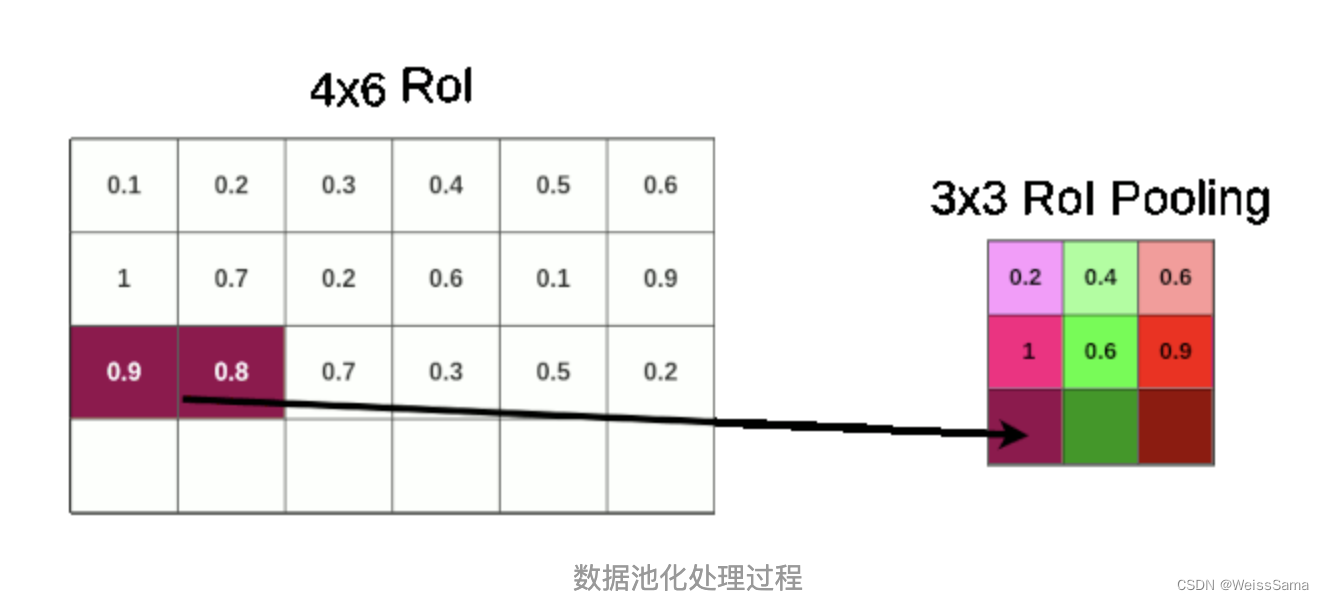
我们最终的到的结果就是3x3xchannel。
这个过程中，我们有两次运算取整，丢失了不少信息。
尤其是对于目标分割这种任务，会损失很多精度。
所以需要改进一下Roi pooling
在分割模型Mask Rcnn中，我们仔细看看这个过程

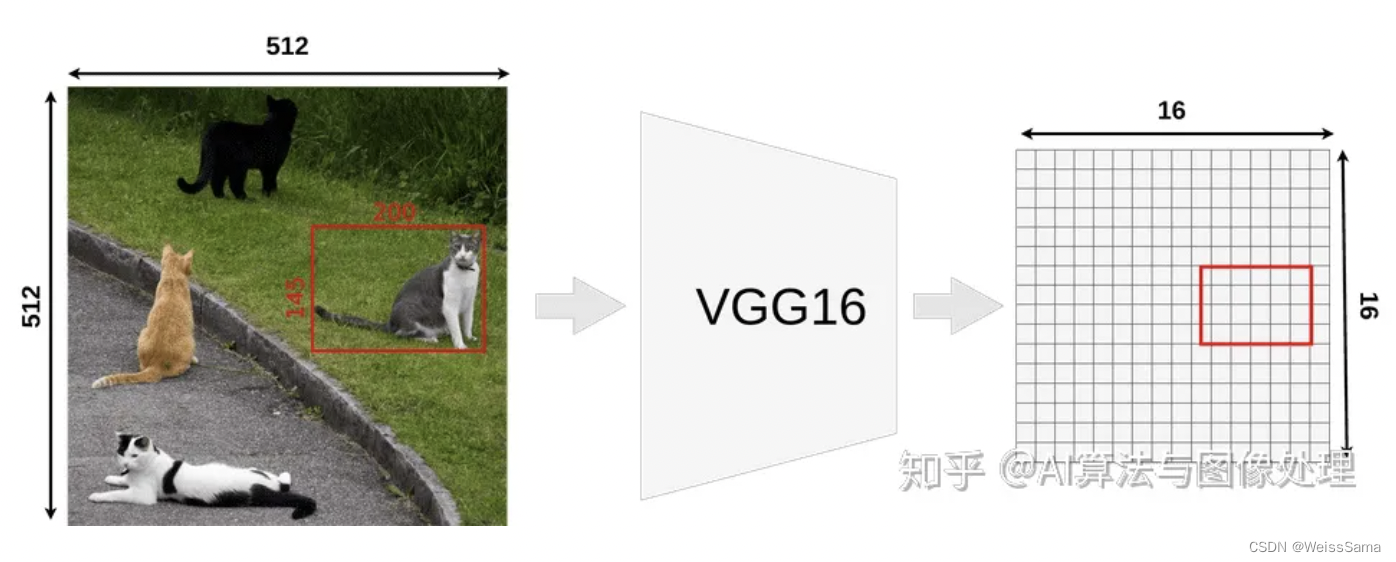
一个512x512x3 的图像经过vgg16的32倍下采样之后，
得到了16x16x512 的feature map。
原图上的一只猫的proposed RoIs (145x200 box)，尝试将其映射到feature map上。
因为不是所有的对象维度都可以整除以32，所以我们没有将RoI与网格对齐。

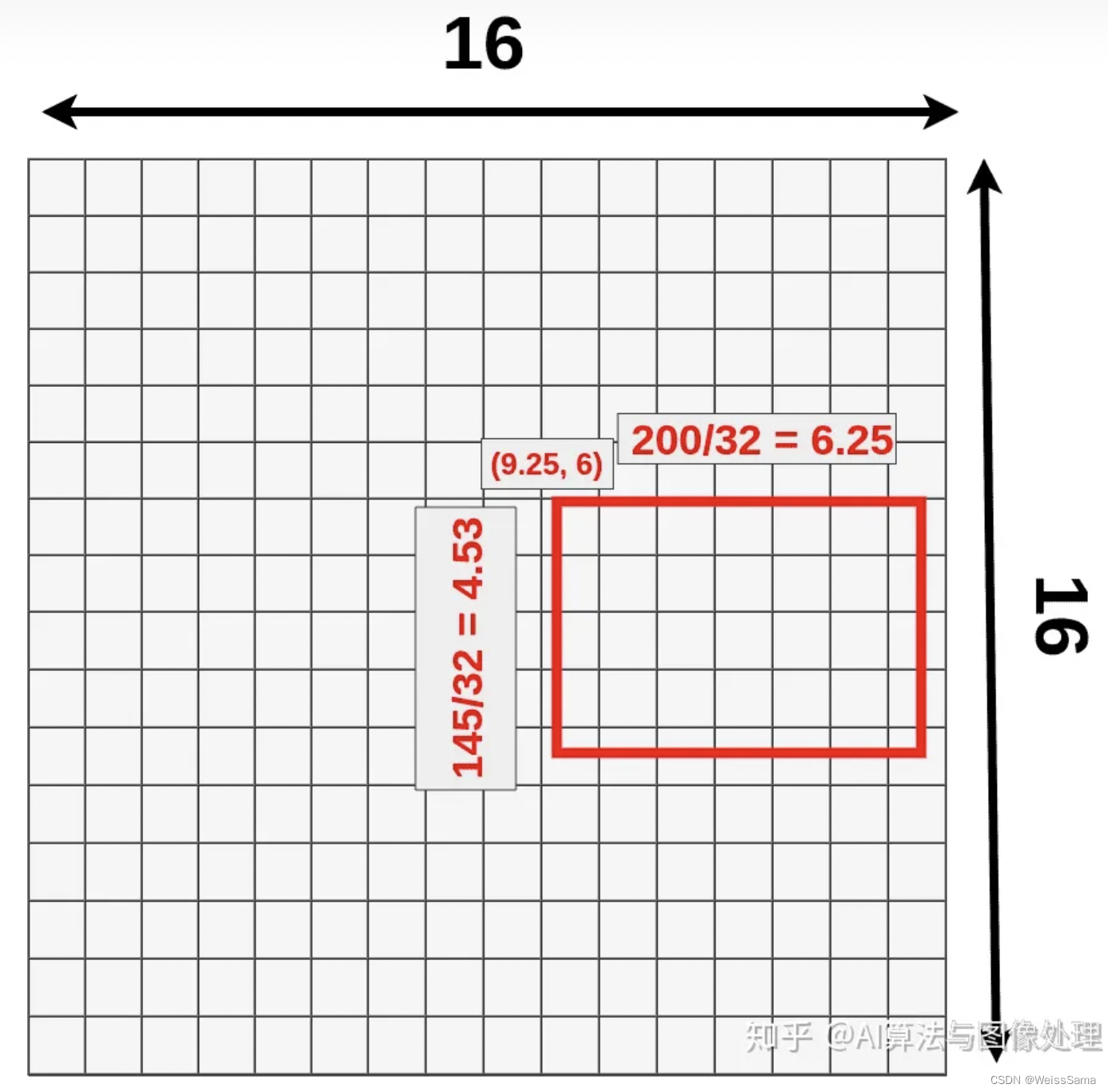
RoI 位置
- (9.25,6) — top left corner
- 6.25 — width
- 4.53 — height
再一次，我们选择池化层的大小为3x3，所以最终的形状是3x3x512
(这只是一个任意的例子，以便更容易在图像上显示）

下面我们引入Roi Align
RoI池化和RoI Align之间的主要区别是量化。RoI Align没有将量化用于数据池化。你知道Fast R-CNN应用了两次量化。
第一次在映射过程中，第二次在池化过程中。

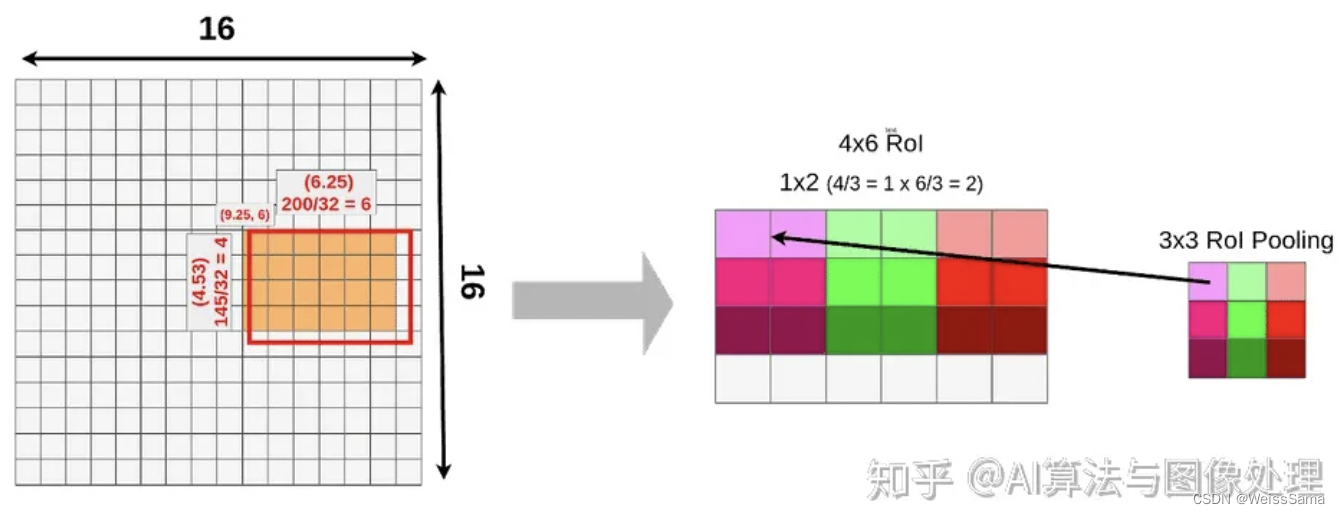
上面是feature map上猫的roi 映射的精确位置。
我们不做量化，直接将原图上的roi划分为k*k相同大小格子，
这里的k是有Roi pooling的大小决定，
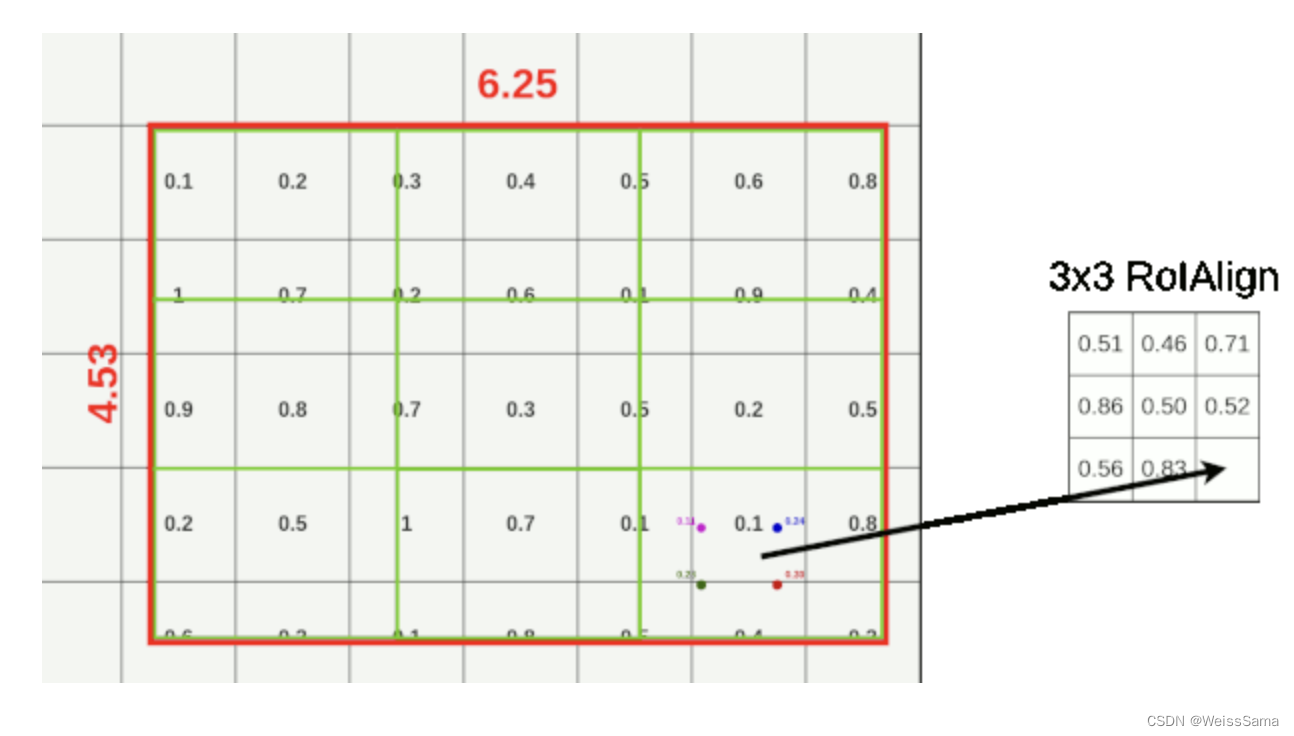
并在每个格子内应用双线性插值，如下图
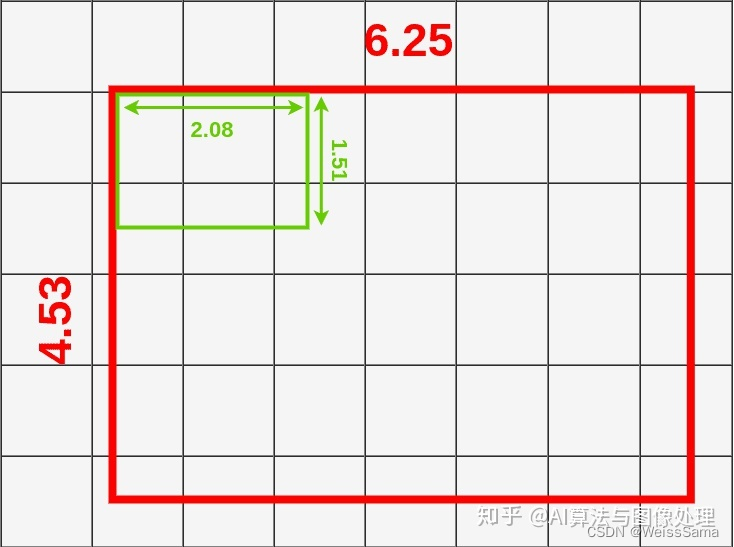
每个格子的大小 = (6.25x4.53)除以3。
这样我们就得到了9个 大约 高为 1.51 ，宽为 2.08 的方框

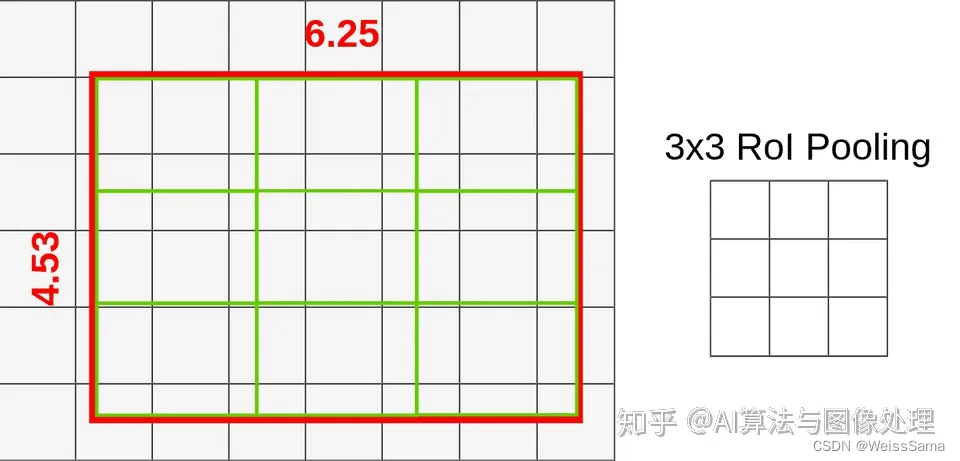
如果查看第一个框(左上角)，可以注意到它覆盖了6个不同的网格单元格。
为了提取池化层的值，我们必须从池化层中采样一些数据。
为了对数据进行采样，我们必须在盒子里创建 四个采样点。我们知道这个9x9的大框的左上角坐标X_box，Y_box 
那么我们计算第一个采样点(左上角)的坐标如下:
- X1 = X_box + (width/3) * 1 = 9.94
- Y1 = Y_box + (height/3) * 1 = 6.50
为了计算第二点(左下角)，我们只需要改变Y:
- X2 = X_box + (width/3) * 1 = 9.94
- Y2 = Y_box + (height/3) * 2 = 7.01

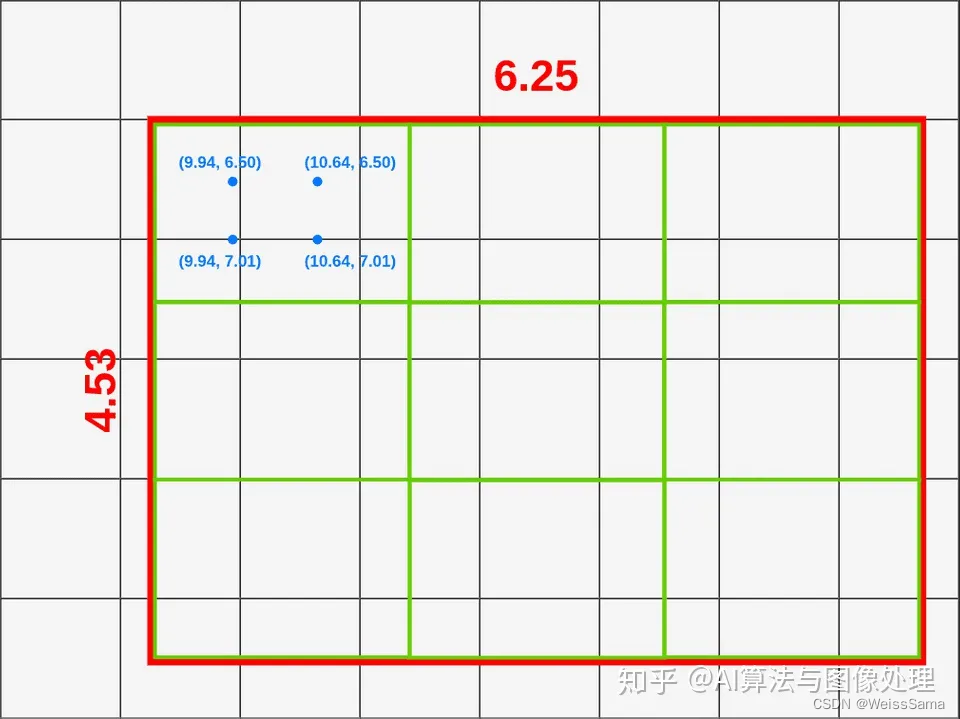
有了这几个采样点的坐标之后，我们就可以进行双线性插值方程计算.
下面是方程。注意代入采样点计算更容易理解。
我们姑且称这9个小格为格子，每个格子占据了feature map上的多个像素值，
我们在每个格子上设置了4个中心位置的采样点，
这些采样点和像素根据它们相应的位置有某种数值关系，
我们计算出这四个采样点对应的像素值，然后对这四个像素值进行max pooling操作，
这样9个格子得到了9个结果。

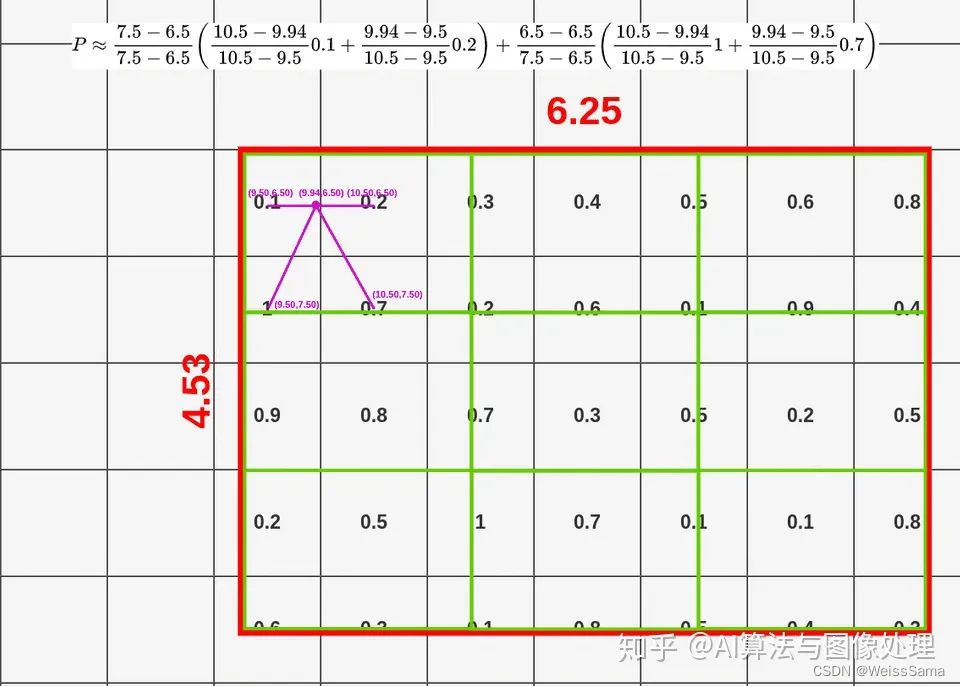
具体的计算过程我今天没时间去完全弄清楚了。不过总体就是我上面写的那样。
下次把这里补上去，今天先直接把计算结果贴上去。

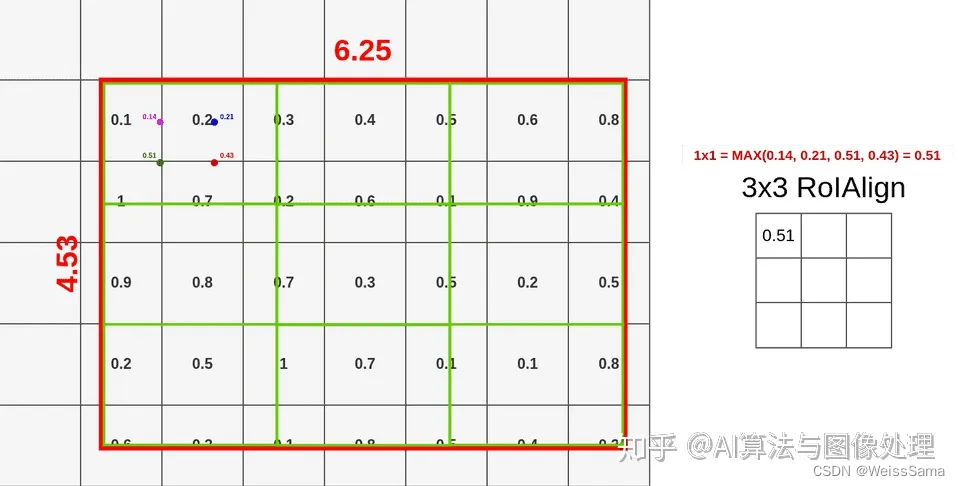
TensorRT的优化原理

1. 算子融合（网络层合并）：简单来说就是通过融合一些计算op或者去掉一些多余op来减少数据流通次数以及显存的频繁使用来提速，融合之后的计算图的层次更少了，占用的CUDA核心数也少了，因此整个模型结构会更小，更快，更高效
2. 低精度量化：量化即IN8量化或者FP16以及TF32等不同于常规FP32精度的使用，这些精度可以显著提升模型执行速度并且不会保持原先模型的精度，更低的数据精度将会使得内存占用和延迟更低，模型体积更小
3. cuda核自动调整：根据不同的显卡构架、SM数量、内核频率等，选择不同的优化策略以及计算方式，寻找最合适当前构架的计算方式，不同的硬件TensorRT 都会做对应的优化，得到优化后的engine
4. 动态张量显存：在每个tensor的使用期间，TensorRT会为其指定显存，避免显存重复申请，减少内存占用和提高重复使用效率
5. 多流执行：使用CUDA中的stream技术，最大化实现并行操作

分别介绍anchor-based和anchor-free的优缺点

Anchor-based方法的优点：

1. 比较精准：Anchor-based方法使用先验框作为基础，可以在更精细的位置上预测目标的位置。Anchor-based方法可以生成不同大小和比例的先验框，也可以更好地检测小目标。
2. 易于训练：由于Anchor-based方法使用预定义的先验框，因此可以通过较少的训练数据快速训练。

Anchor-based方法的缺点：

1. 速度慢：由于需要生成大量的先验框，Anchor-based方法通常需要更长的推理时间。
   容易出现误检：由于使用的是预定义的先验框，可能会导致在目标周围产生多个框，从而导致误检。

Anchor-free方法的优点：

1. 速度快：Anchor-free方法不需要生成大量的先验框，因此推理速度较快。
2. 鲁棒性更好：由于不需要预定义的先验框，Anchor-free方法对目标尺寸和比例的变化更加鲁棒。

Anchor-free方法的缺点：

1. 定位精度相对较低：由于Anchor-free方法不使用预定义的先验框，因此可能无法在更精细的位置上预测目标的位置。
2. 对小目标的检测较差：由于没有预定义的先验框，Anchor-free方法可能无法检测到小目标。

Label Smoothing

label smoothing是一种正则化的方式，全称为Label Smoothing Regularization(LSR)，即标签平滑正则化。
在传统的分类任务计算损失的过程中，是将真实的标签做成one-hot的形式，然后使用交叉熵来计算损失。而label smoothing是将真实的one hot标签做一个标签平滑处理，使得标签变成有概率值的soft label.其中，在真实label处的概率值最大，其他位置的概率值是个非常小的数。
通过soft one-hot 标签来引入噪声，减小了真实样本标签的类别在计算损失函数时的权重，从而改善泛化能力差的问题。

defomable conv和dilated conv

可变形卷积和膨胀卷积

简单描述感受野

一个kernel size=3的卷积核，通过在原feature map上划窗，然后计算得到的是一个值，
这个值是通过计算原来feature map上3×3面积上的值得到的结果，
那就说经过这个3×3卷积以后，这一层feature map的感受野就是3×3。
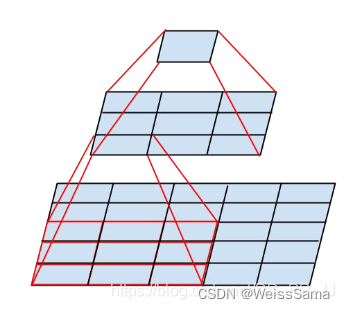
如果是两个kernel size=3的卷积核堆叠起来，那么上图黄色的feature map每个值对应最下面的5×5的感受野。
如下图

简述softmax和cross entropy loss之间关系

softmax公式我就不说了。
softmax早期一般用在分类层，假设你的WX=[1,2,3]，那么经过softmax层后就会得到[0.09,0.24,0.67]，这三个数字表示这个样本属于第1,2,3类的概率分别是0.09,0.24,0.67。
下面是softmax loss

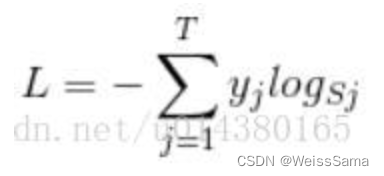
先放一张超不清的softmax loss 图压压惊。
首先L是损失。Sj是softmax的输出向量S的第j个值，前面已经介绍过了，表示的是这个样本属于第j个类别的概率。yj前面有个求和符号，j的范围也是[1,T]，T是类别个数，因此y是一个1*T的向量，里面的T个值，而且只有1个值是1，其他T-1个值都是0。那么哪个位置的值是1呢？答案是真实标签对应的位置的那个值是1，其他都是0。所以这个公式其实有一个更简单的形式：

来举个例子吧。假设一个5分类问题，然后一个样本I的标签y=[0,0,0,1,0]，
也就是说样本I的真实标签是4，
假设模型预测的结果概率（softmax的输出）p=[0.1,0.15,0.05,0.6,0.1]，
可以看出这个预测是对的，那么对应的损失L=-log(0.6)，
也就是当这个样本经过这样的网络参数产生这样的预测p时，它的损失是-log(0.6)。
那么换成p=[0.15,0.2,0.4,0.1,0.15]，这个预测结果就很离谱了，
因为真实标签是4，而你觉得这个样本是4的概率只有0.1
0.1远不如其他概率高，如果是在测试阶段，那么模型就会预测该样本属于类别3，
这样对应损失L=-log(0.1)。
那么再假设p=[0.05,0.15,0.4,0.3,0.1]，这个预测结果虽然也错了，但是没有前面那个那么离谱，
对应的损失L=-log(0.3)。我们知道log函数在输入小于1的时候是个负数，而且log函数是递增函数，
所以-log(0.6) < -log(0.3) < -log(0.1)。
简单讲就是你预测错比预测对的损失要大，预测错得离谱比预测错得轻微的损失要大。

下面是corss entropy loss

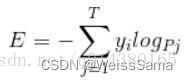
是不是觉得和softmax loss的公式很像。
当cross entropy的输入P是softmax的输出时，cross entropy等于softmax loss。
Pj是输入的概率向量P的第j个值，所以如果你的概率是通过softmax公式得到的，
那么cross entropy就是softmax loss。

在实际代码里面
nn.NLLLoss (负对数似然损失，用于多分类，要求label为稀疏编码，输入经过nn.LogSoftmax激活)
多分类模型：通常推荐使用nn.CrossEntropyLoss(y_pred未经过nn.softmax) == y_pred(经过softmax) + nn.NLLLoss

简述Focal Loss

参考 https://blog.csdn.net/W1995S/article/details/115308674
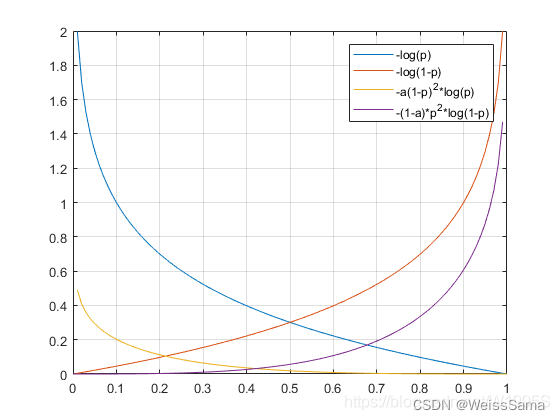
下图是二分类总的cross entropy loss，
有时候我们也只写正样本loss，因为y一般是one-hot表达形式，y不是0就是1
正负样本loss本就对称。
y’ 是经过 sigmoid 激活函数的预测输出（数值在0-1之间）
二分类时候，输出值越大，经过sigmoid越接近1，在蓝色曲线中loss越小。

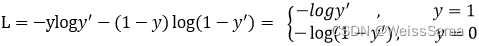
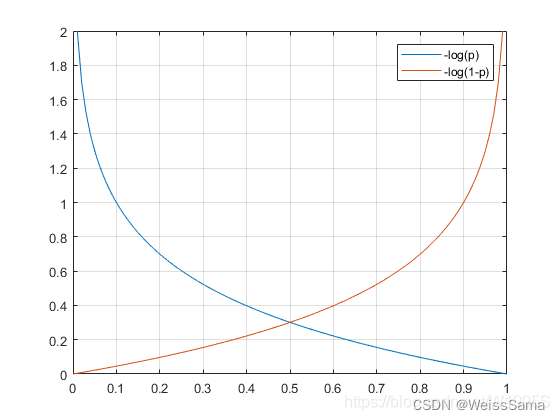
focal loss一共引入了两个参数，第一个是γ\gammaγ，并且γ\gammaγ>0，
见下图2，预测的预测值再大，在整个loss的贡献却变小了。其实就是降低了易分样本在loss中的比重。

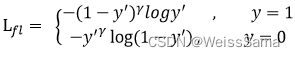
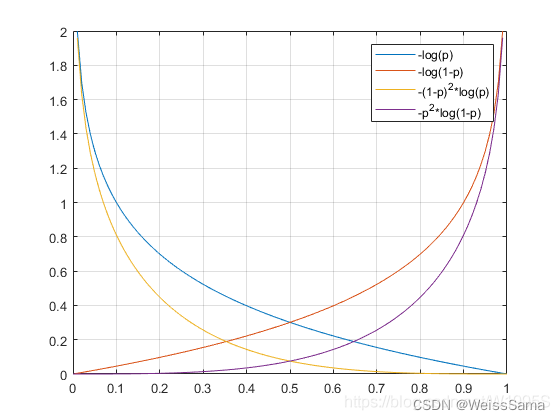
第二个参数是α\alphaα，用来乘以二分cross entropy loss，
用来平衡正负样本本身的数量比例不均（即类别不均衡）