前言

如果你对这篇文章可感兴趣，可以点击「【访客必读 - 指引页】一文囊括主页内所有高质量博客」，查看完整博客分类与对应链接。

变分推断

在贝叶斯方法中，针对含有隐变量的学习和推理，通常有两类方式，其一是马尔可夫链蒙特卡罗法 (MCMC)，其通过采样来近似估计后验概率分布；其二是变分推断，通过解析的方法近似计算后验概率分布。

假设联合概率分布 p(x,z)p(x,z)p(x,z)，其中 xxx 是观测变量，即数据，zzz 是隐变量，目标是学习后验概率分布 p(z∣x)p(z\mid x)p(z∣x)。

由于 p(z∣x)p(z\mid x)p(z∣x) 通常非常复杂，难以直接求解，因此变分推断使用分布 q(z)q(z)q(z) 来近似 p(z∣x)p(z\mid x)p(z∣x)，并通过限制 q(z)q(z)q(z) 形式，得到一种局部最优、但具有确定解的近似后验分布。其中 q(z)q(z)q(z) 即为变分分布 (variational distribution)，q(z)q(z)q(z) 与 p(z∣x)p(z\mid x)p(z∣x) 之间的相似度通过 KL\text{KL}KL 散度衡量。

如下图所示，我们希望在集合 Q\mathcal{Q}Q 中找到 q∗(z)q^*(z)q∗(z) 使其与 p(z∣x)p(z\mid x)p(z∣x) 之间的 KL\text{KL}KL 散度尽可能小。

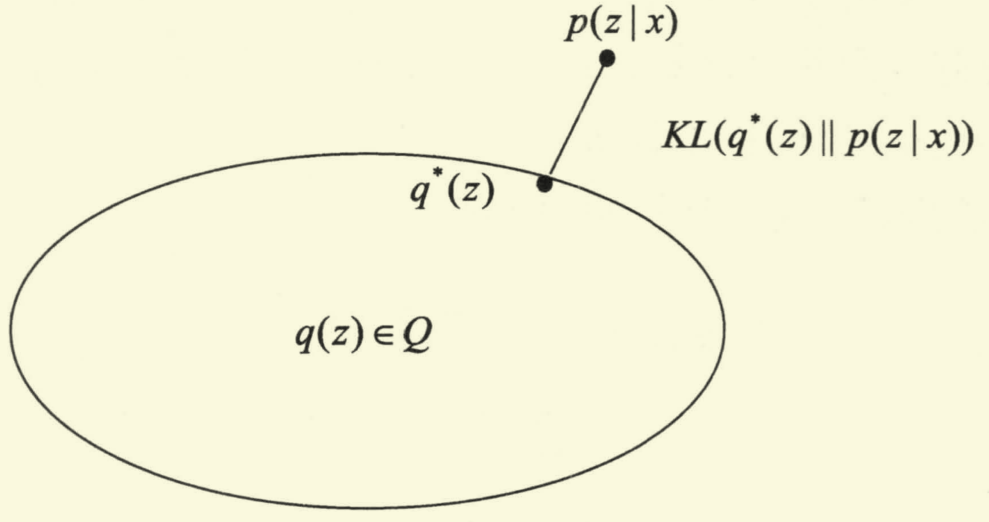
基于上述想法，对 KL(q(z)∥p(z∣x))\text{KL}(q(z)\|p(z\mid x))KL(q(z)∥p(z∣x)) 进行拆解：
KL(q(z)∥p(z∣x))=∫q(z)log⁡q(z)dz−∫q(z)log⁡p(z∣x)dz=log⁡p(x)−{∫q(z)log⁡p(x,z)dz−∫q(z)log⁡q(z)dz}=log⁡p(x)−Eq[log⁡p(x,z)−log⁡q(z)].\begin{aligned} \text{KL}(q(z)\| p(z\mid x)) &= \int q(z) \log q(z) \text{d} z - \int q(z) \log p(z\mid x) \text{d} z \\ &= \log p(x) - \left\{\int q(z) \log p(x,z) \text{d} z - \int q(z) \log q(z) \text{d} z\right\} \\ &= \log p(x) - \mathbb{E}_q\left[\log p(x,z)-\log q(z)\right]. \end{aligned} KL(q(z)∥p(z∣x))​=∫q(z)logq(z)dz−∫q(z)logp(z∣x)dz=logp(x)−{∫q(z)logp(x,z)dz−∫q(z)logq(z)dz}=logp(x)−Eq​[logp(x,z)−logq(z)].​

由于 KL\text{KL}KL 散度非负，因此：
log⁡p(x)≥Eq[log⁡p(x,z)−log⁡q(z)].\log p(x) \geq \mathbb{E}_q\left[\log p(x,z)-\log q(z)\right]. logp(x)≥Eq​[logp(x,z)−logq(z)].

不等式左端为证据 (Evidence)，右端则为证据下界 (Evidence Lower Bound, ELBO\text{ELBO}ELBO)，记作 L(q)L(q)L(q)（ELBO 经常出现于各类与贝叶斯有关的文章中）。

我们的目的是求解 q(z)q(z)q(z) 来最小化 KL(q(z)∥p(z∣x))\text{KL}(q(z)\| p(z\mid x))KL(q(z)∥p(z∣x))，由于 log⁡p(x)\log p(x)logp(x) 是常量，问题转化为最大化 ELBO\text{ELBO}ELBO L(q)L(q)L(q).

若 q(z)q(z)q(z) 形式过于复杂，最大化 ELBO\text{ELBO}ELBO 依然难以求解，因此通常会对 q(z)q(z)q(z) 形式进行约束，一种常见的方式是假设 zzz 服从分布
q(z)=∏iqi(zi),q(z)=\prod_{i} q_i(z_i), q(z)=i∏​qi​(zi​),

即 zzz 可拆解为一系列相互独立的 ziz_izi​，此时的变分分布称为平均场 (Mean Filed).

总结一下，变分推断常见步骤如下：

• 定义变分分布 q(z)q(z)q(z)；
• 推导证据下界 ELBO\text{ELBO}ELBO 表达式；
• 最大化 ELBO\text{ELBO}ELBO，得到 q∗(z)q^*(z)q∗(z)，作为后验概率分布 p(z∣x)p(z\mid x)p(z∣x) 的近似。

广义 EM

上述变分推断过程可以与「广义 EM」联系起来，由于 log⁡p(x)≥ELBO\log p(x)\geq \text{ELBO}logp(x)≥ELBO 恒成立，若将模型参数 θ\thetaθ 引入其中，即可得到：

log⁡p(x∣θ)≥Eq[log⁡p(x,z∣θ)−log⁡q(z)],\log p(x\mid \theta) \geq \mathbb{E}_q\left[\log p(x,z\mid \theta)-\log q(z)\right], logp(x∣θ)≥Eq​[logp(x,z∣θ)−logq(z)],

此时有两种理解：

• 用分布 q(z)q(z)q(z) 近似联合概率分布 p(x,z∣θ)p(x,z\mid \theta)p(x,z∣θ)，最小化分布距离 KL(q∥p)\text{KL}(q\|p)KL(q∥p)；
• 采用极大似然估计的思想，最大化对数似然函数 log⁡p(x∣θ)\log p(x\mid \theta)logp(x∣θ)（也可以理解为最大化证据）。

虽然两种视角不同，但结论一致，即最大化 ELBO\text{ELBO}ELBO，记作 L(q,θ)L(q,\theta)L(q,θ)。对应于广义 EM 算法，即采用迭代的方式，循环执行 E 步和 M 步，直至收敛：

• 【E 步】固定 θ\thetaθ，求 L(q,θ)L(q,\theta)L(q,θ) 对 qqq 的最大化；
• 【M 步】固定 qqq，求 L(q,θ)L(q,\theta)L(q,θ) 对 θ\thetaθ 的最大化。

上述迭代可以保证 log⁡p(x∣θ(t))\log p(x\mid \theta^{(t)})logp(x∣θ(t)) 不降，即一定会收敛，但可能会收敛到局部最优：
log⁡p(x∣θ(t−1))=L(q(t),θ(t−1))≤L(q(t),θ(t))≤log⁡p(x∣θ(t))\log p(x \mid \theta^{(t-1)})=L(q^{(t)}, \theta^{(t-1)}) \leq L(q^{(t)}, \theta^{(t)}) \leq \log p(x \mid \theta^{(t)}) logp(x∣θ(t−1))=L(q(t),θ(t−1))≤L(q(t),θ(t))≤logp(x∣θ(t))

其中「左边第一个等号」由变分推断原理 + E 步得到，「左边第一个不等号」由 M 步得到，「左边第二个不等号」由变分推断原理得到。

参考资料

• 周志华. (2016). 机器学习. 清华大学出版社, 北京.
• 李航. (2019). 统计学习方法. 清华大学出版社, 第 2 版, 北京.