linux办公网
Scikit-network-10：Embedding
创始人
2024-05-30 15:28:55
0次

Embedding

  • https://scikit-network.readthedocs.io/en/stable/reference/embedding.html

Spectral

介绍图的谱嵌入

from IPython.display import SVG
import numpy as np
from scipy import sparse
from sknetwork.data import karate_club, painters, movie_actor
from sknetwork.embedding import Spectral
from sknetwork.visualization import svg_graph, svg_digraph, svg_bigraph

图

graph = karate_club(metadata=True)
adjacency = graph.adjacency
labels = graph.labels# embedding in dimension 2
spectral = Spectral(2)
embedding = spectral.fit_transform(adjacency)
embedding

array([[-0.89876639,  0.43842784],[-0.30788795,  0.95142262],[ 0.04238223,  0.99910147],[-0.3441381 ,  0.93891904],[-0.82105705, -0.57084615],[-0.73816864, -0.67461624],[-0.73816864, -0.67461624],[-0.34568408,  0.93835096],[ 0.73618645,  0.67677878],[ 0.78358705,  0.62128201],[-0.82105705, -0.57084615],[-0.85986949,  0.51051392],[-0.51782927,  0.85548398],[-0.22290148,  0.97484098],[ 0.90007317, -0.43573879],[ 0.90007317, -0.43573879],[-0.66856684, -0.74365206],[-0.51516599,  0.85709043],[ 0.90007317, -0.43573879],[-0.28066995,  0.95980434],[ 0.90007317, -0.43573879],[-0.51516599,  0.85709043],[ 0.90007317, -0.43573879],[ 0.77997798, -0.62580696],[ 0.68984248, -0.7239595 ],[ 0.6717557 , -0.74077276],[ 0.8252923 , -0.56470578],[ 0.87212272, -0.4892872 ],[ 0.99996837, -0.00795388],[ 0.81142925, -0.58445066],[ 0.77271246,  0.63475622],[ 0.75614343, -0.65440593],[ 0.91271077, -0.40860622],[ 0.94609416, -0.32389172]])

# visualization
image = svg_graph(adjacency, position=embedding, labels=labels)
SVG(image)

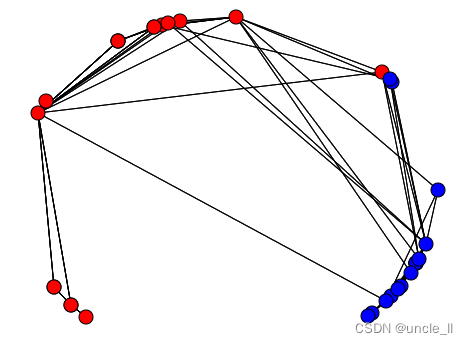
在这里插入图片描述

# find the embedding of a new node
adjacency_vector = np.zeros(adjacency.shape[0], dtype = int)
adjacency_vector, adjacency_vector.shape

(array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]),(34,))

adjacency_vector[:6] = np.ones(6, dtype = int)
adjacency_vector

array([1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])

embedding_vector = spectral.predict(adjacency_vector)
embedding_vector

array([-0.97908533,  0.20345003])

# visualization
adjacency_extend = sparse.vstack([adjacency, adjacency_vector])
adjacency_extend = sparse.hstack([adjacency_extend, sparse.csr_matrix((35, 1))], format='csr')
embedding_extend = np.vstack([embedding, embedding_vector])
labels_extend = list(labels) + [-1]

image = svg_graph(adjacency_extend, position=embedding_extend, labels=labels_extend, seeds={34:1})
SVG(image)

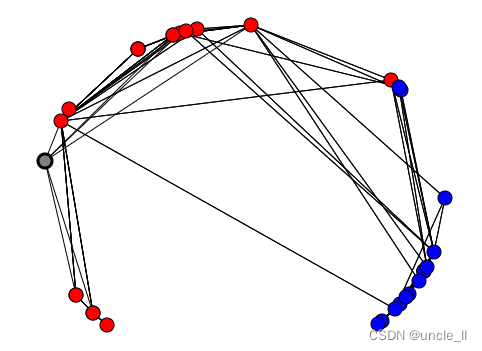
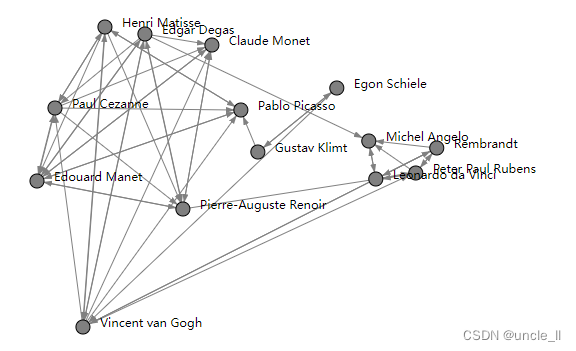
在这里插入图片描述

有向图

graph = painters(metadata=True)
adjacency = graph.adjacency
position = graph.position
names = graph.names

# embedding
spectral = Spectral()  # 默认是2维
embedding = spectral.fit_transform(adjacency)

image = svg_digraph(adjacency, position=embedding, names=names)
SVG(image)

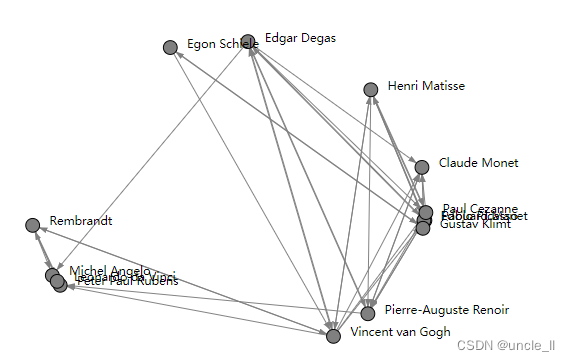
在这里插入图片描述

二部图

graph = movie_actor(metadata=True)
biadjacency = graph.biadjacency
names_row = graph.names_row
names_col = graph.names_col

# embedding
spectral = Spectral(2)
spectral.fit(biadjacency)

Spectral(n_components=2, decomposition='rw', regularization=-1, normalized=True)

embedding_row = spectral.embedding_row_
embedding_col = spectral.embedding_col_

image = svg_bigraph(biadjacency, names_row, names_col,position_row=embedding_row, position_col=embedding_col,color_row='blue', color_col='red')
SVG(image)

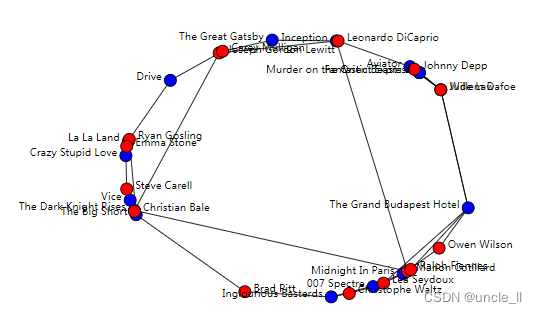
在这里插入图片描述

SVD

通过邻接矩阵的奇异值分解表示图的嵌入

  • https://en.wikipedia.org/wiki/Singular_value_decomposition
from IPython.display import SVG
import numpy as np
from sknetwork.data import karate_club, painters, movie_actor
from sknetwork.embedding import SVD, cosine_modularity
from sknetwork.visualization import svg_graph, svg_digraph, svg_bigraph

图

graph = karate_club(metadata=True)
adjacency = graph.adjacency
labels = graph.labels

svd = SVD(2)
embedding = svd.fit_transform(adjacency)
embedding

array([[-2.390928  ,  1.92543628],[-1.78876603,  1.33853197],[-2.13334091,  0.65279087],[-1.42033097,  1.25893017],[-0.51094331,  0.6664152 ],[-0.53457894,  0.72494643],[-0.53457894,  0.72494643],[-1.14982359,  1.03990599],[-1.52944994, -0.27381159],[-0.69055597, -0.23942952],[-0.51094331,  0.6664152 ],[-0.35549144,  0.38686107],[-0.56667116,  0.6398069 ],[-1.52318706,  0.66931691],[-0.68200769, -0.6951449 ],[-0.68200769, -0.6951449 ],[-0.15896609,  0.29131429],[-0.62145136,  0.6558006 ],[-0.68200769, -0.6951449 ],[-0.99481483,  0.28521152],[-0.68200769, -0.6951449 ],[-0.62145136,  0.6558006 ],[-0.68200769, -0.6951449 ],[-1.00965214, -1.08025878],[-0.38371747, -0.28076981],[-0.39820485, -0.37569412],[-0.50832429, -0.57716769],[-0.89772699, -0.51288909],[-0.88158982, -0.34166407],[-0.90770568, -1.02815711],[-1.17537152, -0.48121995],[-1.28483587, -0.50882896],[-2.07584773, -1.61533845],[-2.51112984, -1.84444934]])

image = svg_graph(adjacency, embedding, labels=labels)
SVG(image)

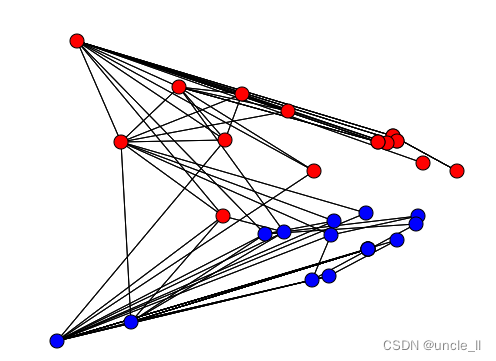
在这里插入图片描述

有向图

graph = painters(metadata=True)
adjacency = graph.adjacency
names = graph.namessvd = SVD(2)
embedding = svd.fit_transform(adjacency)image = svg_digraph(adjacency, embedding, names=names)
SVG(image)

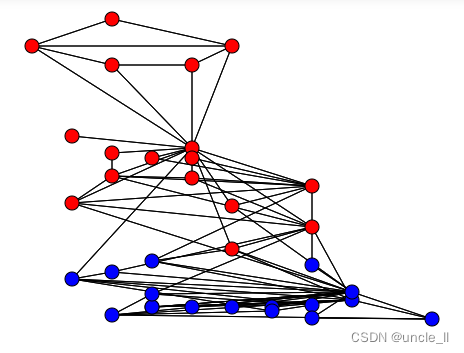
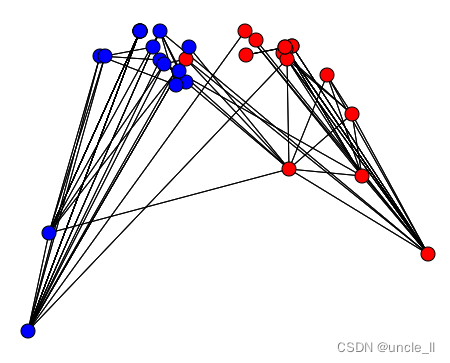
在这里插入图片描述

二部图

graph = movie_actor(metadata=True)
biadjacency = graph.biadjacency
names_row = graph.names_row
names_col = graph.names_colsvd = SVD(2, normalized=False)
svd.fit(biadjacency)embedding_row = svd.embedding_row_
embedding_col = svd.embedding_col_image = svg_bigraph(biadjacency, names_row, names_col,position_row=embedding_row, position_col=embedding_col,color_row='blue', color_col='red', scale=1.5)
SVG(image)

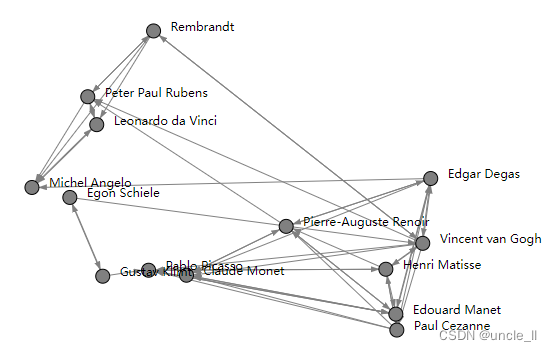
在这里插入图片描述

GSVD

通过邻接矩阵的广义奇异值分解表示图的嵌入

  • https://en.wikipedia.org/wiki/Generalized_singular_value_decomposition
from IPython.display import SVGimport numpy as np
from sknetwork.data import karate_club, painters, movie_actor
from sknetwork.embedding import GSVD
from sknetwork.visualization import svg_graph, svg_digraph, svg_bigraph

图

graph = karate_club(metadata=True)
adjacency = graph.adjacency
labels = graph.labelsgsvd = GSVD(2, normalized=False)
embedding = gsvd.fit_transform(adjacency)image = svg_graph(adjacency, embedding, labels=labels)
SVG(image)

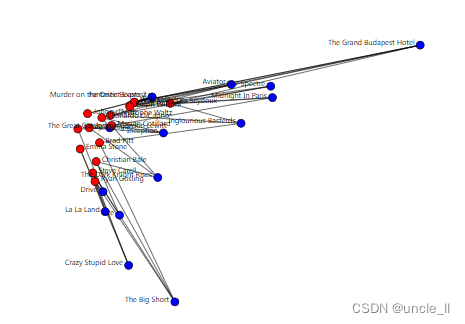
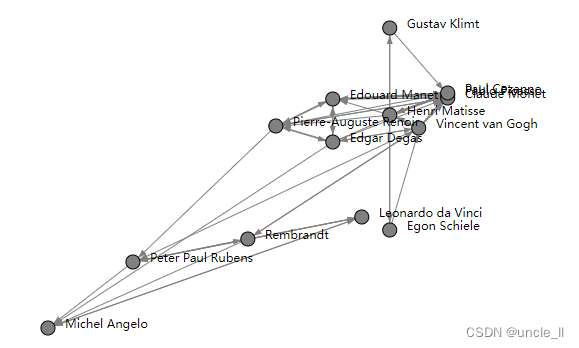
在这里插入图片描述

有向图

graph = painters(metadata=True)
adjacency = graph.adjacency
position = graph.position
names = graph.namesgsvd = GSVD(2, normalized=False)
embedding = gsvd.fit_transform(adjacency)image = svg_digraph(adjacency, embedding, names=names)
SVG(image)

在这里插入图片描述

二部图

graph = movie_actor(metadata=True)
biadjacency = graph.biadjacency
names_row = graph.names_row
names_col = graph.names_colgsvd = GSVD(2, normalized=False)
gsvd.fit(biadjacency)

GSVD(n_components=2, regularization=None, factor_row=0.5, factor_col=0.5, factor_singular=0.0, normalized=False, solver=LanczosSVD(n_iter=None, tol=0.0))

embedding_row = gsvd.embedding_row_
embedding_col = gsvd.embedding_col_image = svg_bigraph(biadjacency, names_row, names_col,position_row=embedding_row, position_col=embedding_col,color_row='blue', color_col='red')
SVG(image)

在这里插入图片描述

PCA

通过邻接矩阵的主成分分析表示图的嵌入

  • https://en.wikipedia.org/wiki/Principal_component_analysis
import numpy as np
from IPython.display import SVG
from sknetwork.embedding import PCA
from sknetwork.data import karate_club, painters, movie_actor
from sknetwork.visualization import svg_graph, svg_digraph, svg_bigraph

图

graph = karate_club(metadata=True)
adjacency = graph.adjacency
labels = graph.labelspca = PCA(2)
embedding = pca.fit_transform(adjacency)image = svg_graph(adjacency, embedding, labels=labels)
SVG(image)

在这里插入图片描述

有向图

graph = painters(metadata=True)
adjacency = graph.adjacency
names = graph.namespca = PCA(2)
embedding = pca.fit_transform(adjacency)image = svg_digraph(adjacency, embedding, names=names)
SVG(image)

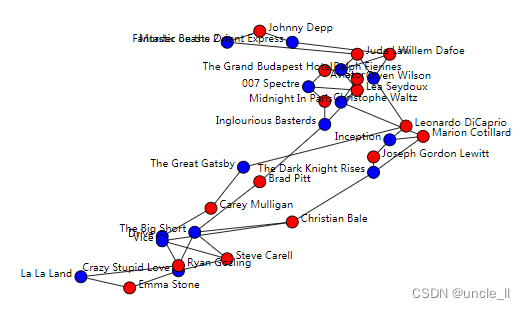
在这里插入图片描述

二部图

graph = movie_actor(metadata=True)
biadjacency = graph.biadjacency
names_row = graph.names_row
names_col = graph.names_colpca = PCA(2)
pca.fit(biadjacency)

PCA(n_components=2, normalized=False, solver=LanczosSVD(n_iter=None, tol=0.0))

embedding_row = pca.embedding_row_
embedding_col = pca.embedding_col_image = svg_bigraph(biadjacency, names_row, names_col,position_row=embedding_row, position_col=embedding_col,color_row='blue', color_col='red')
SVG(image)

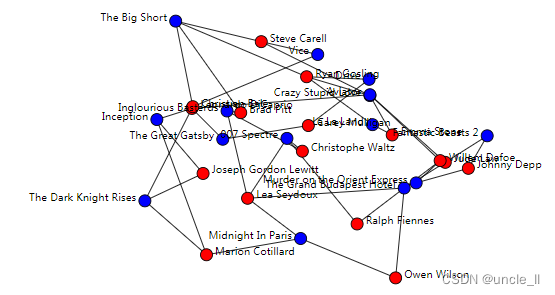
在这里插入图片描述

Random Projection

通过随机投影表示图的嵌入

from IPython.display import SVG
import numpy as np
from sknetwork.data import karate_club, painters, movie_actor
from sknetwork.embedding import RandomProjection
from sknetwork.visualization import svg_graph, svg_digraph, svg_bigraph

图

graph = karate_club(metadata=True)
adjacency = graph.adjacency
labels = graph.labelsprojection = RandomProjection(2)
embedding = projection.fit_transform(adjacency)image = svg_graph(adjacency, position=embedding, labels=labels)
SVG(image)

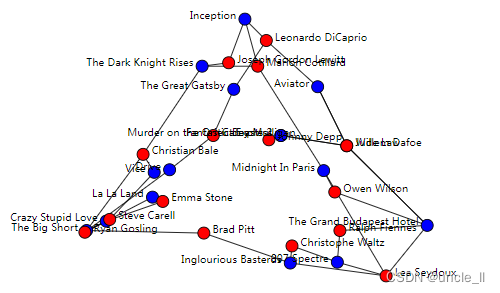
在这里插入图片描述

有向图

graph = painters(metadata=True)
adjacency = graph.adjacency
position = graph.position
names = graph.namesprojection = RandomProjection(2)
embedding = projection.fit_transform(adjacency)image = svg_digraph(adjacency, position=embedding, names=names)
SVG(image)

在这里插入图片描述

二部图

graph = movie_actor(metadata=True)
biadjacency = graph.biadjacency
names_row = graph.names_row
names_col = graph.names_colprojection = RandomProjection(2, normalized=False)
projection.fit(biadjacency)embedding_row = projection.embedding_row_
embedding_col = projection.embedding_col_image = svg_bigraph(biadjacency, names_row, names_col,position_row=embedding_row, position_col=embedding_col,color_row='blue', color_col='red')
SVG(image)

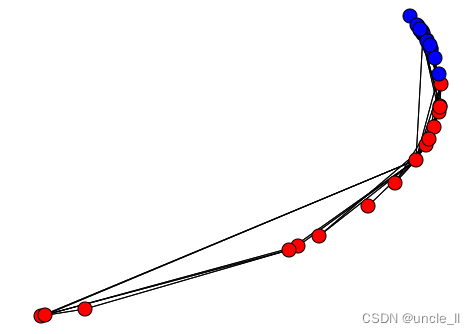
在这里插入图片描述

Louvain

通过Louvain聚类表示图的嵌入

from IPython.display import SVG
import numpy as np
from sknetwork.data import karate_club, painters, movie_actor
from sknetwork.embedding import LouvainEmbedding
from sknetwork.visualization import svg_graph, svg_digraph, svg_bigraph

图

graph = karate_club(metadata=True)
adjacency = graph.adjacency
labels = graph.labelslouvain = LouvainEmbedding()
embedding = louvain.fit_transform(adjacency)
embedding.shape

(34, 4)

position = embedding[:, :2]
image = svg_graph(adjacency, position=position, labels=labels)
SVG(image)

在这里插入图片描述

有向图

graph = painters(metadata=True)
adjacency = graph.adjacency
names = graph.nameslouvain = LouvainEmbedding()
embedding = louvain.fit_transform(adjacency)
embedding.shape

(14, 3)

position = embedding[:, :2]
image = svg_digraph(adjacency, position=position, names=names)
SVG(image)

在这里插入图片描述

二部图

graph = movie_actor(metadata=True)
biadjacency = graph.biadjacency
names_row = graph.names_row
names_col = graph.names_collouvain = LouvainEmbedding()
louvain.fit(biadjacency)

LouvainEmbedding(resolution=1, modularity='dugue', tol_optimization=0.001, tol_aggregation=0.001, n_aggregations=-1, shuffle_nodes=False, isolated_nodes='remove')

embedding_row = louvain.embedding_row_
embedding_col = louvain.embedding_col_
embedding_row.shape

(15, 4)

position_row = embedding_row[:, :2]
position_col = embedding_col[:, :2]

image = svg_bigraph(biadjacency, names_row, names_col,position_row=position_row, position_col=position_col,color_row='blue', color_col='red')
SVG(image)

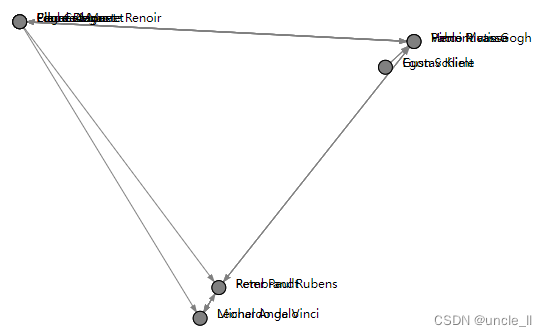
在这里插入图片描述

Hierarchical Louvain

使用分层Louvain算法表示图的嵌入

from IPython.display import SVG
import numpy as np
from sknetwork.data import karate_club, painters, movie_actor
from sknetwork.embedding import LouvainNE
from sknetwork.visualization import svg_graph, svg_digraph, svg_bigraph

图

graph = karate_club(metadata=True)
adjacency = graph.adjacency
labels = graph.labelslouvain = LouvainNE(2)
embedding = louvain.fit_transform(adjacency)image = svg_graph(adjacency, position=embedding, labels=labels)
SVG(image)

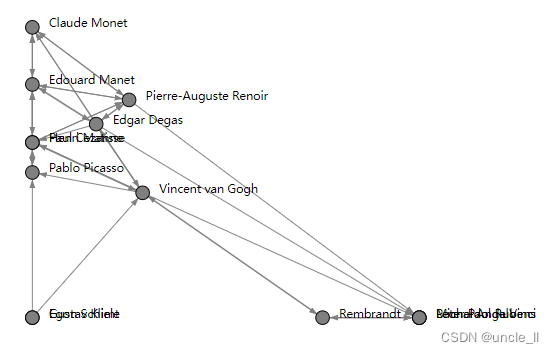
在这里插入图片描述

有向图

graph = painters(metadata=True)
adjacency = graph.adjacency
position = graph.position
names = graph.nameslouvain = LouvainNE(2)
embedding = louvain.fit_transform(adjacency)image = svg_digraph(adjacency, position=embedding, names=names)
SVG(image)

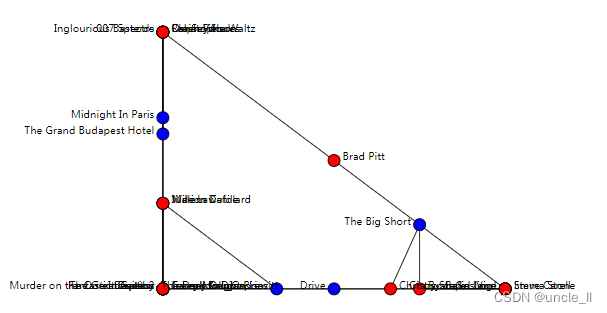
在这里插入图片描述

二部图

graph = movie_actor(metadata=True)
biadjacency = graph.biadjacency
names_row = graph.names_row
names_col = graph.names_collouvain = LouvainNE()
louvain.fit(biadjacency)embedding_row = louvain.embedding_row_
embedding_col = louvain.embedding_col_image = svg_bigraph(biadjacency, names_row, names_col,position_row=embedding_row, position_col=embedding_col,color_row='blue', color_col='red')
SVG(image)

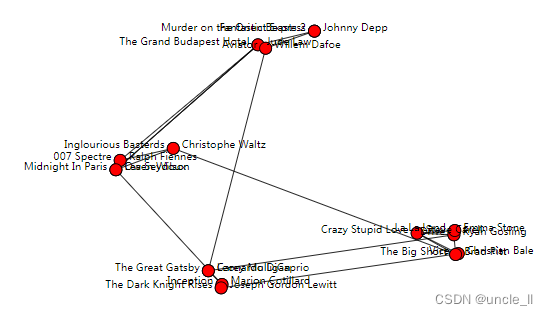
在这里插入图片描述

Spring

通过力定向算法表示图的二维嵌入

  • force-directed algorithm
from IPython.display import SVG
import numpy as np
from sknetwork.data import karate_club, painters
from sknetwork.embedding import Spring
from sknetwork.visualization import svg_graph, svg_digraph

图

graph = karate_club(metadata=True)
adjacency = graph.adjacency
labels = graph.labelsspring = Spring(2)
embedding = spring.fit_transform(adjacency)image = svg_graph(adjacency, position=embedding, labels=labels)
SVG(image)

在这里插入图片描述

有向图

graph = painters(metadata=True)
adjacency = graph.adjacency
names = graph.namesspring = Spring(2)
embedding = spring.fit_transform(adjacency)
embedding.shapeimage = svg_digraph(adjacency, position=embedding, names=names)
SVG(image)

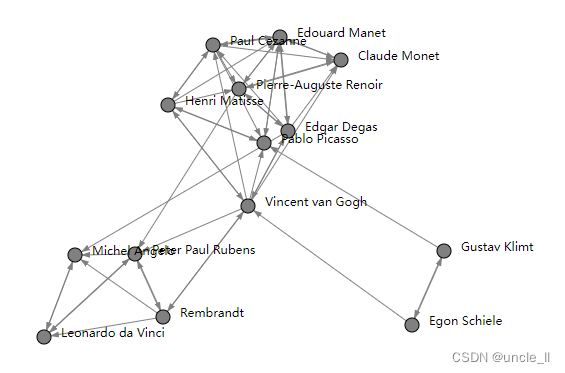
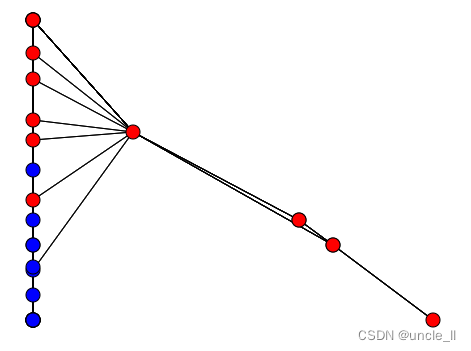
在这里插入图片描述

ForceAtlas

通过力量定向算法 Atlas2 表示图的嵌入

from IPython.display import SVGfrom sknetwork.data import karate_club
from sknetwork.embedding.force_atlas import ForceAtlas
from sknetwork.visualization import svg_graph

graph = karate_club(metadata=True)
adjacency = graph.adjacency
labels = graph.labelsforceatlas2 = ForceAtlas()
embedding = forceatlas2.fit_transform(adjacency)
image = svg_graph(adjacency, embedding, labels=labels)
SVG(image)

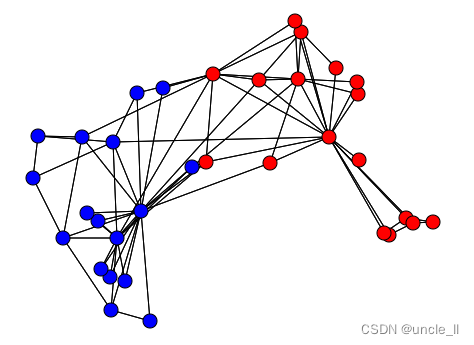
在这里插入图片描述

# 这里介绍不同设置下对图嵌入表示的影响# 用对数吸引力代替线性吸引力（默认是线性吸引力）
forceatlas2 = ForceAtlas(lin_log = True)
embedding = forceatlas2.fit_transform(adjacency)
image = svg_graph(adjacency, embedding, labels=labels)
SVG(image)

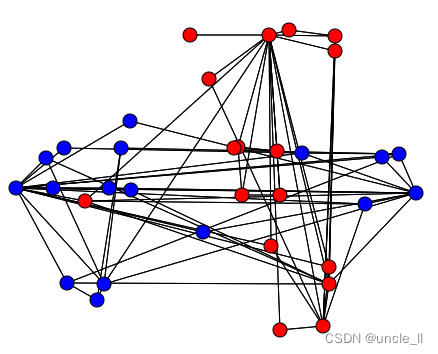
在这里插入图片描述

# 设置重力和斥力常数(重力系数和斥力系数)来设置布局中每个力的重要性，将值保持在0.01和0.1之间
forceatlas2 = ForceAtlas(gravity_factor = 0.1)
embedding = forceatlas2.fit_transform(adjacency)
image = svg_graph(adjacency, embedding, labels=labels)
SVG(image)

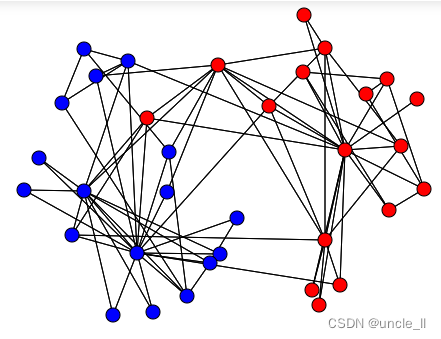
在这里插入图片描述

# 设置摆动容许量，较低的摆动产生较低的速度和更高的精度
forceatlas2 = ForceAtlas(tolerance=1.5)
embedding = forceatlas2.fit_transform(adjacency)
image = svg_graph(adjacency, embedding, labels=labels)
SVG(image)

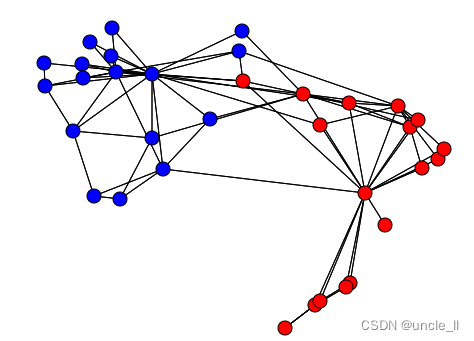
在这里插入图片描述

# 设置近似范围，如果提供了正值，则仅在此距离内使用给定节点的节点来计算排斥力
forceatlas2 = ForceAtlas(approx_radius=2)
embedding = forceatlas2.fit_transform(adjacency)
image = svg_graph(adjacency, embedding, labels=labels)
SVG(image)

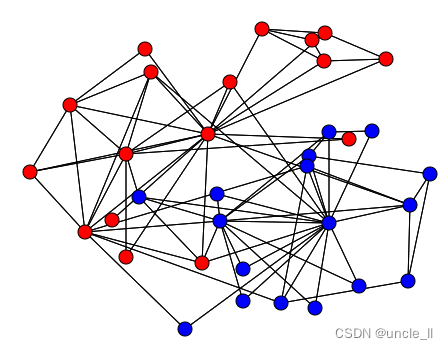
在这里插入图片描述

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：Stimulsoft Dashboards.WEB 23.1.8 完美Patch

下一篇：【GO】K8s 管理系统项目34[Linux环境–应用部署]

相关内容

热门资讯

【NI Multisim 14...   目录 序言 一、工具栏 🍊1.“标准”工具栏 🍊 2.视图工具...
银河麒麟V10SP1高级服务器... 银河麒麟高级服务器操作系统简介： 银河麒麟高级服务器操作系统V10是针对企业级关键业务...
不能访问光猫的的管理页面 光猫是现代家庭宽带网络的重要组成部分，它可以提供高速稳定的网络连接。但是，有时候我们会遇到不能访问光...
AWSECS：访问外部网络时出... 如果您在AWS ECS中部署了应用程序，并且该应用程序需要访问外部网络，但是无法正常访问，可能是因为...
Android|无法访问或保存... 这个问题可能是由于权限设置不正确导致的。您需要在应用程序清单文件中添加以下代码来请求适当的权限：此外...
北信源内网安全管理卸载 北信源内网安全管理是一款网络安全管理软件，主要用于保护内网安全。在日常使用过程中，卸载该软件是一种常...
AWSElasticBeans... 在Dockerfile中手动配置nginx反向代理。例如，在Dockerfile中添加以下代码：FR...
AsusVivobook无法开... 首先，我们可以尝试重置BIOS（Basic Input/Output System）来解决这个问题。...
ASM贪吃蛇游戏-解决错误的问... 要解决ASM贪吃蛇游戏中的错误问题，你可以按照以下步骤进行：首先，确定错误的具体表现和问题所在。在贪...
月入8000+的steam搬砖... 大家好，我是阿阳 今天要给大家介绍的是 steam 游戏搬砖项目，目前...