极图

l部图的概念与特征

定义：若简单图G的点集V有一个划分：

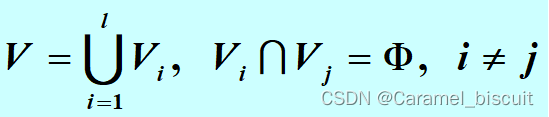
且所有的Vi非空，Vi内的点均不邻接，设G是一个l部图。

1. 如果l=2，则G就是偶图。
2. n阶无环图必是n部图。
3. 若l1

如果在一个l部图G中，|Vi|=ni 任何两点u∈Vi , v∈Vj , i ≠ j , i, j =1, 2,…, l 均邻接，则称G为完全l部图。
记作

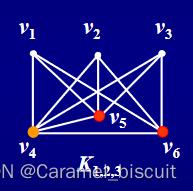
如果在一个n阶完全l部图中，n=kl+r(0≤ r |V1| = |V2| = ··· = |Vr| = k + 1, |Vr+1| = |Vr+2| = ··· = |Vl | = k
则称G为n阶完全l几乎等部图，记为Tl, n。

V1| = |V2| = ··· = |Vl| 的完全l几乎等部图称为完全l等部图。

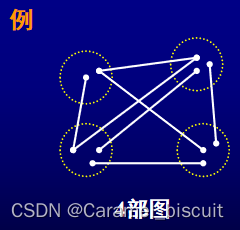
1. 这是一个连通的3部图，点集V的划分为V1={v4}，V2={v3,v5}，V3={v1,v2,v6}；
2. V的划分也可以为V1={v1,v5},V2={v2,v3},V3={v4,v6}；
3. 这也是一个2部图，点集的划分为V1={v2,v4,v6}，V2={v1,v3,v5}；且划分唯一

连通偶图的2部划分是唯一的。
证明：设连通偶图G的2部划分为V1∪V2 =V。
取v∈V1，由于G 连通，对任何u∈V1∪V2， G中有联结u 和v的路，故d (v, u)有定义。
因为任何一条以v为起点的路交替地经过V1和V2的点，可知一个点u∈V2 当且仅当d (v, u)是奇数。
该准则唯一地决定了G的2部划分。

Turán定理

**定义：设G和H是两个n阶图，称G度弱于H，如果存在双射 μ：V (G)→V(H)，使得对任何点v∈V(G)，有
**

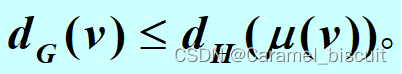
若G度弱于H，一定有m(G) ≤ m(H)。但逆命题不成立。
例如：(1, 1, 2, 4)与(3, 3, 3, 3)没有度弱关系！

若n阶简单图G不包含Kl+1，则G度弱于某个完全l部图H，且若G具有H相同的度序列，则G ≌ H。

设G是n阶简单图，并且不包含Kl+1，则边数m(G)≤ m(Tl, n)。
此外，仅当G ≌ Tl, n时，m(G) = m(Tl, n)。