#D. 竞选班长
创始人
2025-05-30 22:03:29
0次
题目
思路1
可以发现题目问的是
至少有多少人参加了投票
并且题目中有一句
不能弃权或投给其它的人
所以A和B的票数如果从前往后看的话,那么按理来说应该是不递减的(后面一次票数>=前面一次的票数)
可是比例是已约过分的
所以可能不递减
那么我们可以不断将A的票数和B的票数一起*i(i不断+1)
直到A,B的票数都>=AB上一次的票数
最后输出A,B最终的票数和就行了
程序1
#include
#define ll long long
using namespace std;
int n,a[10000001],b[10000001];
signed main()
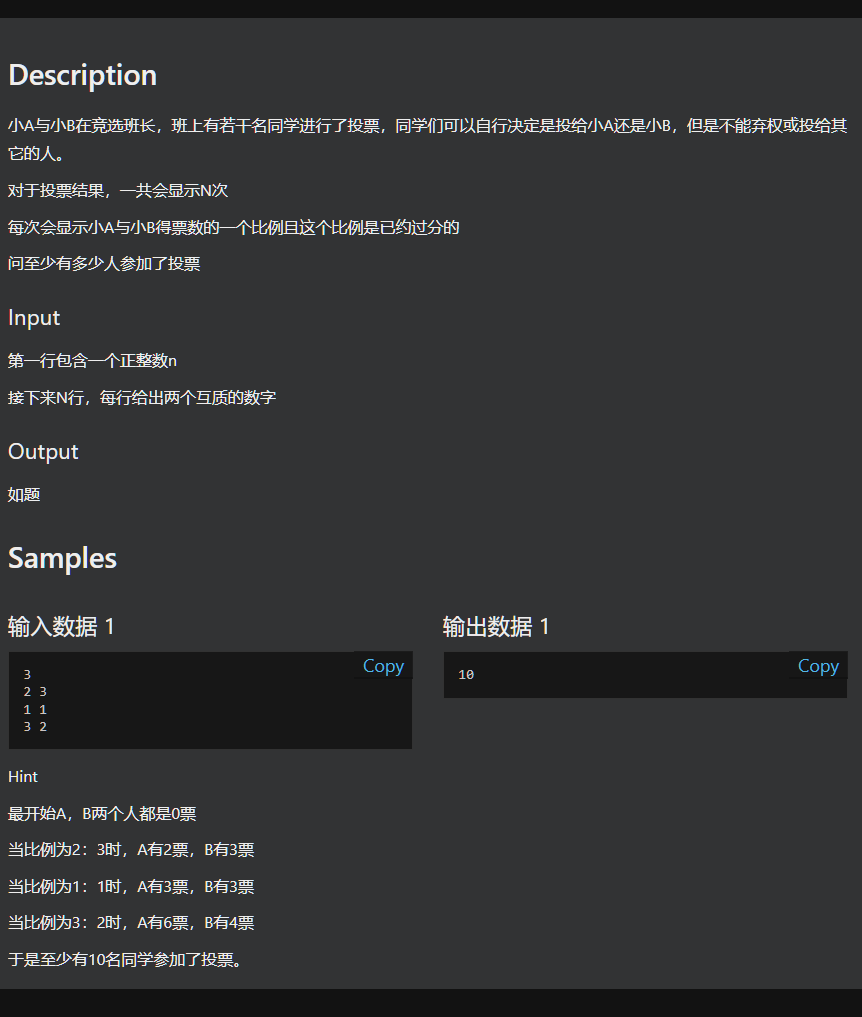
{cin>>n;for(int i = 1;i <= n;i++) cin>>a[i]>>b[i];for(int i = 2;i <= n;i++){int t = a[i],t_2 = b[i];while(a[i] < a[i - 1] || b[i] < b[i - 1])a[i] += t,b[i] += t_2;}cout< 但是,提交上去后,37分,TLE了。。。
思路2
我们可以发现TLE的原因是
int t = a[i],t_2 = b[i];while(a[i] < a[i - 1] || b[i] < b[i - 1])a[i] += t,b[i] += t_2;这段代码要一个个去倍增,那么怎么优化呢?
我们每次处理A,B的票数时可以分3种情况
a[i] < a[i - 1] && b[i] >= b[i - 1]
这样,a[i]不符合条件,但是b[i]符合,所以我们用t记录下a[i - 1]/a[i]并向上取整的结果
a[i] >= a[i - 1] && b[i] < b[i - 1]
这样,b[i]不符合条件,但是a[i]符合,所以我们用t记录下b[i - 1]/b[i]并向上取整的结果
a[i] < a[i - 1] && b[i] < b[i - 1]
这样,a[i]不符合条件,b[i]也符合,所以我们用t记录下max(a[i - 1]/a[i],b[i - 1 / b[i]])并都向上取整的结果
最后将a[i],b[i] * t就行了。
向上取整的原因:如果向下取整,举个例子a[i - 1]=6,a[i] = 4,那么6/4向下取整是1,可是4*1不>=6,只能*2,所以只能向上取整。
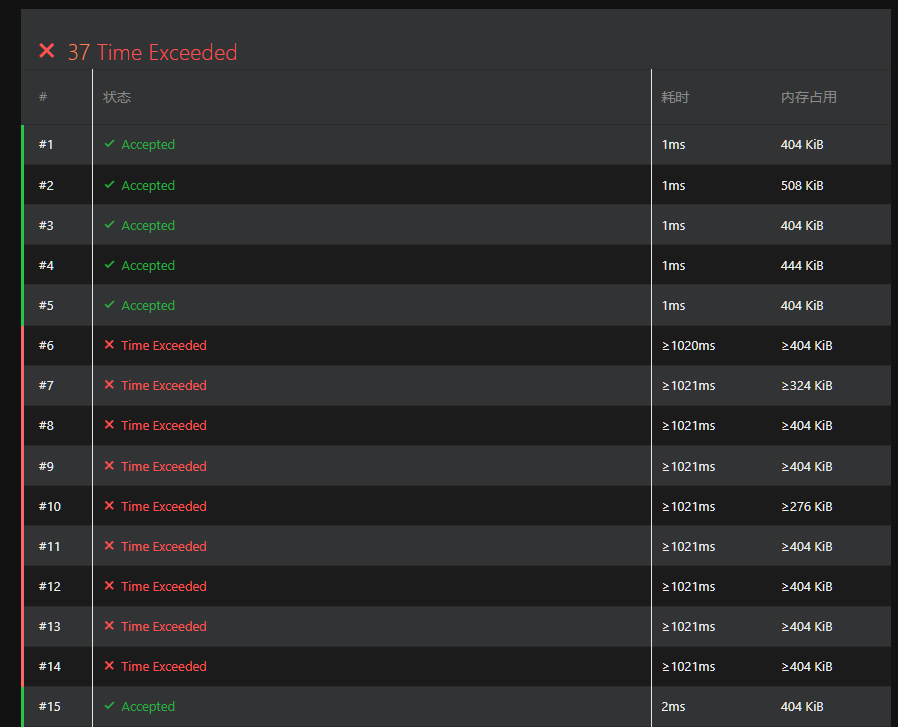
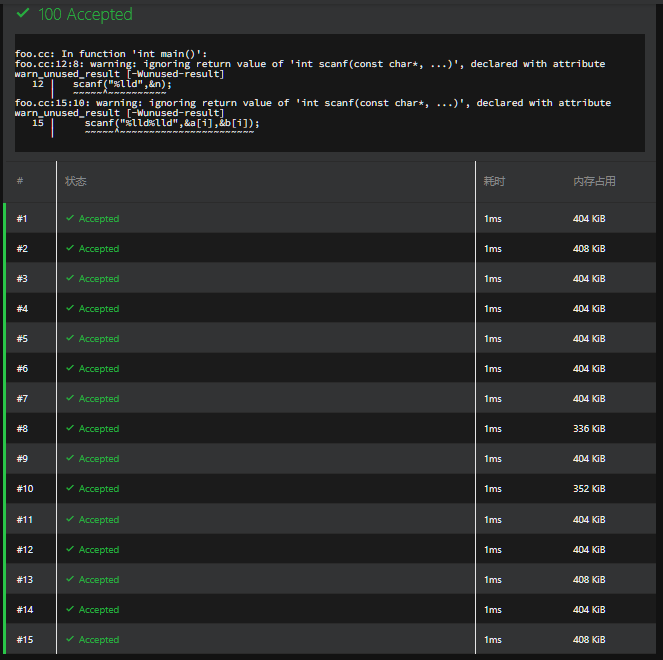
AC代码
#include
#define int long long
using namespace std;
int n,a[10000001],b[10000001],ta[10000001],tb[10000001],t;
int f(int x,int y)//返回x/y的向上取整的结果
{if(x % y != 0) return x / y + 1;else return x / y;
}
signed main()
{scanf("%lld",&n);for(int i = 1; i <= n; i++){scanf("%lld%lld",&a[i],&b[i]);if(i > 1 && ((a[i] < a[i - 1])||(b[i] < b[i - 1])))//只要a[i]/b[i]有一个不符合条件{if(a[i] < a[i - 1] && b[i] >= b[i - 1]) t = f(a[i - 1],a[i]);else if(a[i] >= a[i - 1] && b[i] < b[i - 1]) t = f(b[i - 1],b[i]);else if(a[i] < a[i - 1] && b[i] < b[i - 1]){int tt = f(a[i - 1],a[i]),ttt = f(b[i - 1],b[i]);t = max(ttt,tt);}a[i] *= t;b[i] *= t;}}printf("%lld",a[n] + b[n]);return 0;
} 
相关内容
热门资讯
保存时出现了1个错误,导致这篇...
当保存文章时出现错误时,可以通过以下步骤解决问题:查看错误信息:查看错误提示信息可以帮助我们了解具体...
汇川伺服电机位置控制模式参数配...
1. 基本控制参数设置 1)设置位置控制模式 2)绝对值位置线性模...
不能访问光猫的的管理页面
光猫是现代家庭宽带网络的重要组成部分,它可以提供高速稳定的网络连接。但是,有时候我们会遇到不能访问光...
不一致的条件格式
要解决不一致的条件格式问题,可以按照以下步骤进行:确定条件格式的规则:首先,需要明确条件格式的规则是...
本地主机上的图像未显示
问题描述:在本地主机上显示图像时,图像未能正常显示。解决方法:以下是一些可能的解决方法,具体取决于问...
表格列调整大小出现问题
问题描述:表格列调整大小出现问题,无法正常调整列宽。解决方法:检查表格的布局方式是否正确。确保表格使...
表格中数据未显示
当表格中的数据未显示时,可能是由于以下几个原因导致的:HTML代码问题:检查表格的HTML代码是否正...
Android|无法访问或保存...
这个问题可能是由于权限设置不正确导致的。您需要在应用程序清单文件中添加以下代码来请求适当的权限:此外...
【NI Multisim 14...
目录 序言 一、工具栏 🍊1.“标准”工具栏 🍊 2.视图工具...
银河麒麟V10SP1高级服务器...
银河麒麟高级服务器操作系统简介: 银河麒麟高级服务器操作系统V10是针对企业级关键业务...