【动手学深度学习】(task1)注意力机制(更新中)
note
- 注意力机制
文章目录
- note
- 零、基础回顾
- 0.0 不同人员的学习定位
- 0.1 AI地图
- 0.2 深度学习的应用
- 0.3 答疑
- 一、可视化注意力权重
- 1.1 查询、键和值
- 1.2 注意力的可视化
- 1.3 小结和练习
- 二、注意力汇聚:Nadaraya-Watson 核回归
- 三、注意力评分函数
- 四、Bahdanau 注意力
- 五、多头注意力
- 六、自注意力和位置编码
- 6.1 比较卷积神经网络、循环神经网络和自注意力
- 6.2 位置编码
- (1)绝对位置编码
- (2)相对位置编码
- 七、Transformer架构
- 八、简单栗子
- 时间安排
- Reference
零、基础回顾
0.0 不同人员的学习定位
- AI相关从业人员(产品经理等):掌握What,知道名词,能干什么
- 数据科学家、工程师:掌握What、How,手要快,能出活
- 研究员、学生:掌握What、How、Why,除了知道有什么和怎么做,还要知道为什么,思考背后的原因,做出新的突破
0.1 AI地图
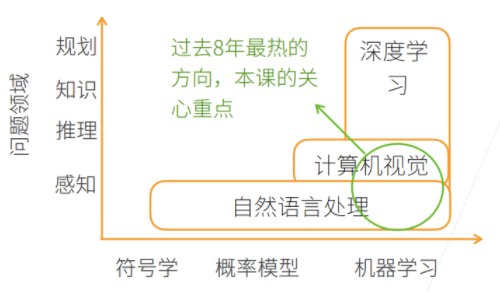
y轴表示可以达到的层次:由底部向上依次是
感知:了解是什么,比如能够可以看到物体,如面前的一块屏幕
推理:基于感知到的现象,想象或推测未来会发生什么
知识:根据看到的数据或者现象,形成自己的知识
规划:根据学习到的知识,做出长远的规划
- NLP:停留在【感知层面】,如机器翻译;NLP从【符号学】的方法,到【概率模型】,到现在的【机器学习|深度学习】。
- CV:在感知层面上,对图片做一些推理;图片里都是像素,很难用nlp的那种符号学解释,所以一般用【概率模型】和【机器学习|深度学习】。
- 深度学习:机器学习的一种,包括CV、NLP、强化学习等。
0.2 深度学习的应用

- 物体检测和分割:图片内容、物体是啥、物体位置;物体分割指每个像素属于什么,属于飞机还是人等;
- 样式迁移:原图片+迁移风格=风格迁移后的图片
- 文生图:如diffusion model
- 文字生成:如ChatGPT
- 广告点击:
- 步骤:
- 触发:用户输入关键词,机器先找到一些相关的广告
- 点击率预估: 利用机器学习的模型预测用户对广告的点击率
- 排序:利用 点击率 x 竞价 的结果进行排序呈现广告,排名高的在前面呈现
- 模型的预测:数据 (待预测广告) → 特征提取 → 模型 → 点击率预测
- 训练数据 (过去广告展现和用户点击) → 特征(X)和用户点击(Y) → 喂给模型训练
- 步骤:
0.3 答疑
◆ Q1:领域专家是什么意思?
举个例子,比如我要做农业上的物体识别,我种了一棵树,想要看今年的收成怎么样,我有很多很多土地,用人去一个个查看很费力,于是我用一个无人机,将农作物的情况拍下来,假设得到了树的一些图片,而数据科学家不知道农作物什么样的情况是好,什么样是坏,于是领域专家进行解释,比如多少叶子算是好,什么样不好。同时数据科学家将领域专家的问题翻译成机器学习能做的任务。所以可以认为领域专家是提需求的人甲方,而数据科学家是乙方。
◆ Q2:符号学可以和机器学习融合起来吗?
确实是可以的。目前来说,符号学在深度学习有一些新的进展,以前说符号学就是做一些符号上的推理,目前深度学习如图神经网络,可以做一些比较复杂的推理。
Q3:说自然语言处理仅仅停留在感知层面似乎不太合适?因为语言的理解和产出不仅仅是感知,也涉及到语言知识和世界知识,也涉及到规划,比如机器规划下一步要做什么。
语言当然是一个很复杂的过程,我只是想说,自然语言处理我们做得还很一般,虽然能做一些感知以外的东西,但是我感觉是说,不如深度学习特别机器学习,在图片上的应用做得好一些。当然AI地图上也只是一个大致的分类。
◆ Q4:如何寻找自己领域的paper的经验吗?
因为大家如果现在去读paper的话,可能每天都有一百篇paper出来,你怎么样去找到你想要的paper,总不能天天看朋友圈推文,这样只能知道别人读过的paper,不会有自己独特的见解。
◆ Q5:以无人驾驶为例,误判率在不断下降,但误判的影响还是很严重的,有可能从已有的判断case(样例)得到修正,从而完全避免这样的错误吗?
无人驾驶中,任何一次出现的错误,都可能带来毁灭性的灾难。大家可能看到,特斯拉今天撞了,明天又撞了。所以说,无人驾驶对于错误率确实是非常注重的。
机器学习在学术界现在有很多关于uncertainty或者robustness的研究,就是说模型在数据偏移或者极端情况下会不会给出很不好的答案,我们不会特别深入去讲这个事情,但是无人驾驶这一块确实会通过大量的技术,比如说把不同的模型融合在一起,不是仅仅train一个模型,用多个模型来做投票。汽车有很多雷达、摄像头,它会通过不同的传感器来进行模型的融合,从而降低误差。
因为涉及到评价无人驾驶的特别技术,但在竞赛中我们会给大家看到如何通过融合多个模型提升精度的做法。
一、可视化注意力权重
1.1 查询、键和值
自主性的与非自主性的注意力提示解释了人类的注意力的方式,下面来看看如何通过这两种注意力提示,用神经网络来设计注意力机制的框架,
首先,考虑一个相对简单的状况,即只使用非自主性提示。要想将选择偏向于感官输入,则可以简单地使用参数化的全连接层,甚至是非参数化的最大汇聚层或平均汇聚层。
因此:
- “是否包含自主性提示”将注意力机制与全连接层或汇聚层区别开来。在注意力机制的背景下,自主性提示被称为查询(query)。给定任何查询,注意力机制通过注意力汇聚(attention pooling)将选择引导至感官输入(sensory inputs,例如中间特征表示)。
- 在注意力机制中,这些感官输入被称为值(value)。更通俗的解释,每个值都与一个键(key)配对,这可以想象为感官输入的非自主提示。如下图所示,可以通过设计注意力汇聚的方式,便于给定的查询(自主性提示)与键(非自主性提示)进行匹配,这将引导得出最匹配的值(感官输入)。
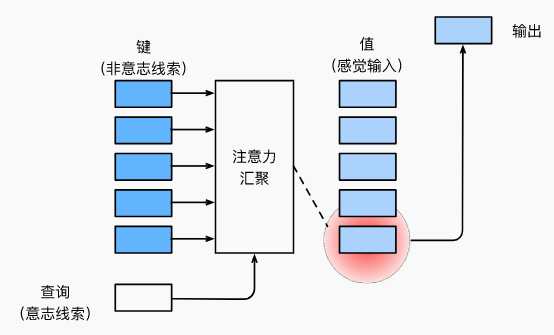
这个框架下的模型将成为本章的中心。然而,注意力机制的设计有许多替代方案。例如可以设计一个不可微的注意力模型,该模型可以使用强化学习方法(Mnih et al., 2014)进行训练。
1.2 注意力的可视化
平均汇聚层可以被视为输入的加权平均值,其中各输入的权重是一样的。实际上,注意力汇聚得到的是加权平均的总和值,其中权重是在给定的查询和不同的键之间计算得出的。
import torch
import matplotlib.pyplot as plt
from matplotlib_inline import backend_inline
# from d2l import torch as d2l# metrices: shape, [要显示的行数,要显示的列数,查询的数目, 键的数目]
# 可视化注意力权重
#@save
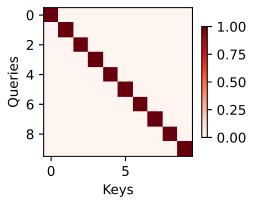
def show_heatmaps(matrices, xlabel, ylabel, titles=None, figsize=(2.5, 2.5),cmap='Reds'):"""显示矩阵热图"""backend_inline.set_matplotlib_formats('svg') # format# d2l.use_svg_display()num_rows, num_cols = matrices.shape[0], matrices.shape[1]# fig, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize,# sharex=True, sharey=True, squeeze=False)fig, axes = plt.subplots(num_rows, num_cols, figsize=figsize,sharex=True, sharey=True, squeeze=False)for i, (row_axes, row_matrices) in enumerate(zip(axes, matrices)):for j, (ax, matrix) in enumerate(zip(row_axes, row_matrices)):pcm = ax.imshow(matrix.detach().numpy(), cmap=cmap)if i == num_rows - 1:ax.set_xlabel(xlabel)if j == 0:ax.set_ylabel(ylabel)if titles:ax.set_title(titles[j])fig.colorbar(pcm, ax=axes, shrink=0.6);# 当查询和键相同时,注意力权重为1,否则为0
attention_weights = torch.eye(10).reshape((1, 1, 10, 10))
# 显示注意力权重
show_heatmaps(attention_weights, xlabel='Keys', ylabel='Queries')
上面的栗子,仅当查询和键相同时,注意力权重为1,否则为0。后面也经常用show_heatmaps函数来显示注意力权重。
1.3 小结和练习
【小结】
- 受试者使用非自主性和自主性提示有选择性地引导注意力。前者基于突出性,后者则依赖于意识。
- 注意力机制与全连接层或者汇聚层的区别源于增加的自主提示。
- 由于包含了自主性提示,注意力机制与全连接的层或汇聚层不同。
- 注意力机制通过注意力汇聚使选择偏向于值(感官输入),其中包含查询(自主性提示)和键(非自主性提示)。键和值是成对的。
- 可视化查询和键之间的注意力权重是可行的。
【练习】
(1)在机器翻译中通过解码序列词元时,其自主性提示可能是什么?非自主性提示和感官输入又是什么?
答:解码序列词元时的自主性提示可能是指模型已经学习到的语言规则
(2)随机生成一个10 X 10矩阵并使用softmax运算来确保每行都是有效的概率分布,然后可视化输出注意力权重。
答:
二、注意力汇聚:Nadaraya-Watson 核回归
【回顾上节】
查询(自主提示)和键(非自主提示)之间的交互形成了注意力汇聚;注意力汇聚有选择地聚合了值(感官输入)以生成最终的输出。1964年提出的Nadaraya-Watson核回归模型是一个简单但完整的例子,可以用于演示具有注意力机制的机器学习。
【小结本节】
- Nadaraya-Watson核回归是具有注意力机制的机器学习范例。
- Nadaraya-Watson核回归的注意力汇聚是对训练数据中输出的加权平均。从注意力的角度来看,分配给每个值的注意力权重取决于将值所对应的键和查询作为输入的函数。
- 注意力汇聚可以分为非参数型和带参数型。
回归问题:给定的成对的“输入-输出”数据集{(x1,y1),…,(xn,yn)}\{(x_1, y_1), \ldots, (x_n, y_n)\}{(x1,y1),…,(xn,yn)},如何学习fff来预测任意新输入xxx的输出y^=f(x)\hat{y} = f(x)y^=f(x)?
【准备数据集】根据下面的非线性函数生成一个人工数据集,其中加入的噪声项为ϵ\epsilonϵ:yi=2sin(xi)+xi0.8+ϵ,y_i = 2\sin(x_i) + x_i^{0.8} + \epsilon,yi=2sin(xi)+xi0.8+ϵ,
其中ϵ\epsilonϵ服从均值为000和标准差为0.50.50.5的正态分布。在这里生成了505050个训练样本和505050个测试样本。为了更好地可视化之后的注意力模式,需要将训练样本进行排序。
import torch
import torch.nn as nn
from d2l import torch as d2l# build dataset
n_train = 50 # 训练样本数
x_train, _ = torch.sort(torch.rand(n_train) * 5) # 排序后的训练样本def f(x):return 2 * torch.sin(x) + x**0.8y_train = f(x_train) + torch.normal(0.0, 0.5, (n_train,)) # 训练样本的输出
x_test = torch.arange(0, 5, 0.1) # 测试样本
y_truth = f(x_test) # 测试样本的真实输出
n_test = len(x_test) # 测试样本数
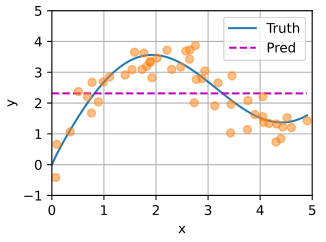
# n_testdef plot_kernel_reg(y_hat):d2l.plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'Pred'],xlim=[0, 5], ylim=[-1, 5])d2l.plt.plot(x_train, y_train, 'o', alpha=0.5)# 和上面和下面的可视化函数结果等价
def use_svg_display():"""Use the svg format to display a plot in Jupyter.Defined in :numref:`sec_calculus`"""backend_inline.set_matplotlib_formats('svg')def set_figsize(figsize=(3.5, 2.5)):"""Set the figure size for matplotlib.Defined in :numref:`sec_calculus`"""use_svg_display()d2l.plt.rcParams['figure.figsize'] = figsizedef set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):"""Set the axes for matplotlib.Defined in :numref:`sec_calculus`"""axes.set_xlabel(xlabel)axes.set_ylabel(ylabel)axes.set_xscale(xscale)axes.set_yscale(yscale)axes.set_xlim(xlim)axes.set_ylim(ylim)if legend:axes.legend(legend)axes.grid()def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,ylim=None, xscale='linear', yscale='linear',fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):"""Plot data points.Defined in :numref:`sec_calculus`"""if legend is None:legend = []set_figsize(figsize)axes = axes if axes else d2l.plt.gca()# Return True if `X` (tensor or list) has 1 axisdef has_one_axis(X):return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)and not hasattr(X[0], "__len__"))if has_one_axis(X):X = [X]if Y is None:X, Y = [[]] * len(X), Xelif has_one_axis(Y):Y = [Y]if len(X) != len(Y):X = X * len(Y)axes.cla()for x, y, fmt in zip(X, Y, fmts):if len(x):axes.plot(x, y, fmt)else:axes.plot(y, fmt)set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)def plot_kernel_reg(y_hat):plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'Pred'],xlim=[0, 5], ylim=[-1, 5])plt.plot(x_train, y_train, 'o', alpha=0.5);# 平均汇聚
y_hat = torch.repeat_interleave(y_train.mean(), n_test)
plot_kernel_reg(y_hat)
三、注意力评分函数
【小结】
- 将注意力汇聚的输出计算可以作为值的加权平均,选择不同的注意力评分函数会带来不同的注意力汇聚操作。
- 当查询和键是不同长度的矢量时,可以使用可加性注意力评分函数。当它们的长度相同时,使用缩放的“点-积”注意力评分函数的计算效率更高。
第二节使用了高斯核来对查询和键之间的关系建模。高斯核指数部分可以视为注意力评分函数(attention scoring function),简称评分函数(scoring function),然后把这个函数的输出结果输入到softmax函数中进行运算。通过上述步骤,将得到与键对应的值的概率分布(即注意力权重)。最后,注意力汇聚的输出就是基于这些注意力权重的值的加权和。
从宏观来看,上述算法可以用来实现对应的注意力机制框架。说明了如何将注意力汇聚的输出计算成为值的加权和,其中aaa表示注意力评分函数。由于注意力权重是概率分布,因此加权和其本质上是加权平均值。
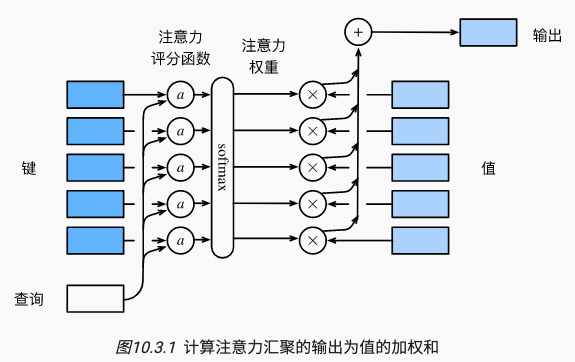
用数学语言描述,假设有一个查询q∈Rq\mathbf{q} \in \mathbb{R}^qq∈Rq和mmm个“键-值”对(k1,v1),…,(km,vm)(\mathbf{k}_1,\mathbf{v}_1), \ldots, (\mathbf{k}_m, \mathbf{v}_m)(k1,v1),…,(km,vm),其中ki∈Rk\mathbf{k}_i \in \mathbb{R}^kki∈Rk,vi∈Rv\mathbf{v}_i \in \mathbb{R}^vvi∈Rv。注意力汇聚函数fff就被表示成值的加权和:
f(q,(k1,v1),…,(km,vm))=∑i=1mα(q,ki)vi∈Rv,f(\mathbf{q}, (\mathbf{k}_1, \mathbf{v}_1), \ldots, (\mathbf{k}_m, \mathbf{v}_m)) = \sum_{i=1}^m \alpha(\mathbf{q}, \mathbf{k}_i) \mathbf{v}_i \in \mathbb{R}^v,f(q,(k1,v1),…,(km,vm))=i=1∑mα(q,ki)vi∈Rv,
其中查询q\mathbf{q}q和键ki\mathbf{k}_iki的注意力权重(标量)是通过注意力评分函数aaa将两个向量映射成标量,再经过softmax运算得到的:
α(q,ki)=softmax(a(q,ki))=exp(a(q,ki))∑j=1mexp(a(q,kj))∈R.\alpha(\mathbf{q}, \mathbf{k}_i) = \mathrm{softmax}(a(\mathbf{q}, \mathbf{k}_i)) = \frac{\exp(a(\mathbf{q}, \mathbf{k}_i))}{\sum_{j=1}^m \exp(a(\mathbf{q}, \mathbf{k}_j))} \in \mathbb{R}.α(q,ki)=softmax(a(q,ki))=∑j=1mexp(a(q,kj))exp(a(q,ki))∈R.
正如上图所示,选择不同的注意力评分函数aaa会导致不同的注意力汇聚操作。本节将介绍两个流行的评分函数,稍后将用他们来实现更复杂的注意力机制。
四、Bahdanau 注意力
【小结】
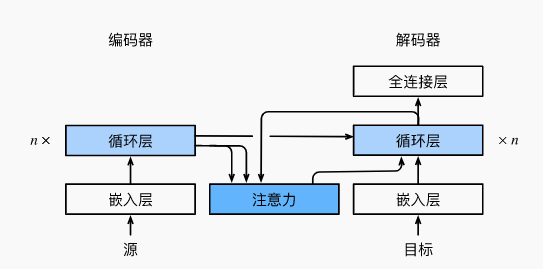
- 在预测词元时,如果不是所有输入词元都是相关的,那么具有Bahdanau注意力的循环神经网络编码器-解码器会有选择地统计输入序列的不同部分。这是通过将上下文变量视为加性注意力池化的输出来实现的。
- 在循环神经网络编码器-解码器中,Bahdanau注意力将上一时间步的解码器隐状态视为查询,在所有时间步的编码器隐状态同时视为键和值。
五、多头注意力
【小结】
- 多头注意力融合了来自于多个注意力汇聚的不同知识,这些知识的不同来源于相同的查询、键和值的不同的子空间表示。
- 基于适当的张量操作,可以实现多头注意力的并行计算。
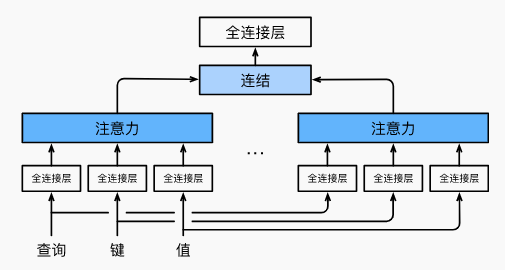
在实现多头注意力之前,让我们用数学语言将这个模型形式化地描述出来。
给定查询q∈Rdq\mathbf{q} \in \mathbb{R}^{d_q}q∈Rdq、键k∈Rdk\mathbf{k} \in \mathbb{R}^{d_k}k∈Rdk和值v∈Rdv\mathbf{v} \in \mathbb{R}^{d_v}v∈Rdv,每个注意力头hi\mathbf{h}_ihi(i=1,…,hi = 1, \ldots, hi=1,…,h)的计算方法为:
hi=f(Wi(q)q,Wi(k)k,Wi(v)v)∈Rpv,\mathbf{h}_i = f(\mathbf W_i^{(q)}\mathbf q, \mathbf W_i^{(k)}\mathbf k,\mathbf W_i^{(v)}\mathbf v) \in \mathbb R^{p_v},hi=f(Wi(q)q,Wi(k)k,Wi(v)v)∈Rpv,
其中,可学习的参数包括Wi(q)∈Rpq×dq\mathbf W_i^{(q)}\in\mathbb R^{p_q\times d_q}Wi(q)∈Rpq×dq、Wi(k)∈Rpk×dk\mathbf W_i^{(k)}\in\mathbb R^{p_k\times d_k}Wi(k)∈Rpk×dk和Wi(v)∈Rpv×dv\mathbf W_i^{(v)}\in\mathbb R^{p_v\times d_v}Wi(v)∈Rpv×dv,以及代表注意力汇聚的函数fff。fff可以是第三节中的加性注意力和缩放点积注意力。多头注意力的输出需要经过另一个线性转换,它对应着hhh个头连结后的结果,因此其可学习参数是Wo∈Rpo×hpv\mathbf W_o\in\mathbb R^{p_o\times h p_v}Wo∈Rpo×hpv:
Wo[h1⋮hh]∈Rpo.\mathbf W_o \begin{bmatrix}\mathbf h_1\\\vdots\\\mathbf h_h\end{bmatrix} \in \mathbb{R}^{p_o}.Woh1⋮hh∈Rpo.
基于这种设计,每个头都可能会关注输入的不同部分,可以表示比简单加权平均值更复杂的函数。
六、自注意力和位置编码
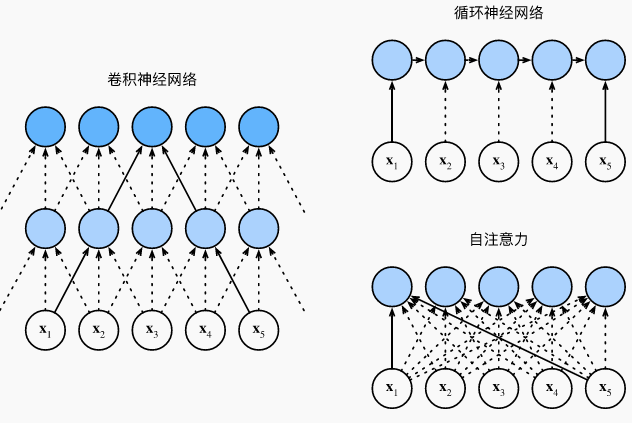
- 在自注意力中,查询、键和值都来自同一组输入。
- 卷积神经网络和自注意力都拥有并行计算的优势,而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
- 为了使用序列的顺序信息,可以通过在输入表示中添加位置编码,来注入绝对的或相对的位置信息。
6.1 比较卷积神经网络、循环神经网络和自注意力
给定一个由词元组成的输入序列x1,…,xn\mathbf{x}_1, \ldots, \mathbf{x}_nx1,…,xn,其中任意xi∈Rd\mathbf{x}_i \in \mathbb{R}^dxi∈Rd(1≤i≤n1 \leq i \leq n1≤i≤n)。该序列的自注意力输出为一个长度相同的序列y1,…,yn\mathbf{y}_1, \ldots, \mathbf{y}_ny1,…,yn,其中:
yi=f(xi,(x1,x1),…,(xn,xn))∈Rd\mathbf{y}_i = f(\mathbf{x}_i, (\mathbf{x}_1, \mathbf{x}_1), \ldots, (\mathbf{x}_n, \mathbf{x}_n)) \in \mathbb{R}^dyi=f(xi,(x1,x1),…,(xn,xn))∈Rd
根据之前定义的注意力汇聚函数fff:f(x)=∑i=1nα(x,xi)yif(x)=\sum_{i=1}^n \alpha\left(x, x_i\right) y_i f(x)=i=1∑nα(x,xi)yi
下面的代码片段是基于多头注意力对一个张量完成自注意力的计算,张量的形状为(批量大小,时间步的数目或词元序列的长度,ddd)。输出与输入的张量形状相同。
6.2 位置编码
在处理词元序列时,循环神经网络是逐个的重复地处理词元的,而自注意力则因为并行计算而放弃了顺序操作。为了使用序列的顺序信息,通过在输入表示中添加位置编码(positional encoding)来注入绝对的或相对的位置信息。位置编码可以通过学习得到也可以直接固定得到。接下来描述的是基于正弦函数和余弦函数的固定位置编码( (Vaswani et al., 2017)。)。
假设输入表示X∈Rn×d\mathbf{X} \in \mathbb{R}^{n \times d}X∈Rn×d包含一个序列中nnn个词元的ddd维嵌入表示。位置编码使用相同形状的位置嵌入矩阵P∈Rn×d\mathbf{P} \in \mathbb{R}^{n \times d}P∈Rn×d输出X+P\mathbf{X} + \mathbf{P}X+P,矩阵第iii行、第2j2j2j列和2j+12j+12j+1列上的元素为:
pi,2j=sin(i100002j/d),pi,2j+1=cos(i100002j/d).\begin{aligned} p_{i, 2j} &= \sin\left(\frac{i}{10000^{2j/d}}\right),\\p_{i, 2j+1} &= \cos\left(\frac{i}{10000^{2j/d}}\right).\end{aligned}pi,2jpi,2j+1=sin(100002j/di),=cos(100002j/di).
在解释这个设计之前,让我们先在下面的PositionalEncoding类中实现它。
(1)绝对位置编码
(2)相对位置编码
除了捕获绝对位置信息之外,上述的位置编码还允许模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移δ\deltaδ,位置i+δi + \deltai+δ处的位置编码可以线性投影位置iii处的位置编码来表示。
这种投影的数学解释是,令ωj=1/100002j/d\omega_j = 1/10000^{2j/d}ωj=1/100002j/d,对于任何确定的位置偏移δ\deltaδ,中的任何一对(pi,2j,pi,2j+1)(p_{i, 2j}, p_{i, 2j+1})(pi,2j,pi,2j+1)都可以线性投影到
(pi+δ,2j,pi+δ,2j+1)(p_{i+\delta, 2j}, p_{i+\delta, 2j+1})(pi+δ,2j,pi+δ,2j+1):
[cos(δωj)sin(δωj)−sin(δωj)cos(δωj)][pi,2jpi,2j+1]=[cos(δωj)sin(iωj)+sin(δωj)cos(iωj)−sin(δωj)sin(iωj)+cos(δωj)cos(iωj)]=[sin((i+δ)ωj)cos((i+δ)ωj)]=[pi+δ,2jpi+δ,2j+1],\begin{aligned} &\begin{bmatrix} \cos(\delta \omega_j) & \sin(\delta \omega_j) \\ -\sin(\delta \omega_j) & \cos(\delta \omega_j) \\ \end{bmatrix} \begin{bmatrix} p_{i, 2j} \\ p_{i, 2j+1} \\ \end{bmatrix}\\ =&\begin{bmatrix} \cos(\delta \omega_j) \sin(i \omega_j) + \sin(\delta \omega_j) \cos(i \omega_j) \\ -\sin(\delta \omega_j) \sin(i \omega_j) + \cos(\delta \omega_j) \cos(i \omega_j) \\ \end{bmatrix}\\ =&\begin{bmatrix} \sin\left((i+\delta) \omega_j\right) \\ \cos\left((i+\delta) \omega_j\right) \\ \end{bmatrix}\\ =& \begin{bmatrix} p_{i+\delta, 2j} \\ p_{i+\delta, 2j+1} \\ \end{bmatrix}, \end{aligned}===[cos(δωj)−sin(δωj)sin(δωj)cos(δωj)][pi,2jpi,2j+1][cos(δωj)sin(iωj)+sin(δωj)cos(iωj)−sin(δωj)sin(iωj)+cos(δωj)cos(iωj)][sin((i+δ)ωj)cos((i+δ)ωj)][pi+δ,2jpi+δ,2j+1],
2×22\times 22×2投影矩阵不依赖于任何位置的索引iii。
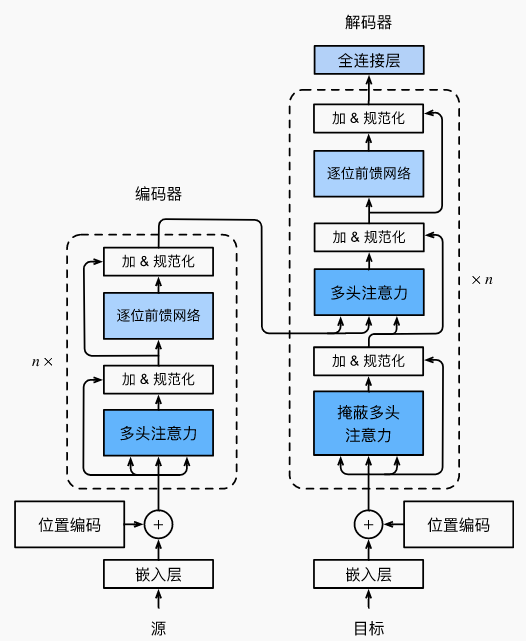
七、Transformer架构
- Transformer是编码器-解码器架构的一个实践,尽管在实际情况中编码器或解码器可以单独使用。
- 在Transformer中,多头自注意力用于表示输入序列和输出序列,不过解码器必须通过掩蔽机制来保留自回归属性。
- Transformer中的残差连接和层规范化是训练非常深度模型的重要工具。
- Transformer模型中基于位置的前馈网络使用同一个多层感知机,作用是对所有序列位置的表示进行转换。
八、简单栗子
时间安排
打卡日:19号周日、21号周二、23号周四、28号周二、30号周四。
| 内容 | 任务 | 预估天数 | 任务时间 | 完成情况 |
|---|---|---|---|---|
| task1 | dl基础+CP10-注意力机制(一) | 一天 | 3月19号周日 | 完成 |
| task2 | CP10-注意力机制(二)10.1-10.4 | 两天 | 3月20、21号周二 | |
| task3 | CP10-注意力机制(三) 10.5-10.7 | 两天 | 3月22号周三、23号周四 | |
| task4 | CP14-预训练(一)14.8-14.9 | 两天 | 3月24号周五、25号周六 | |
| task5 | CP14-预训练(二) 14.10 | 两天 | 3月26周日、27、28周二 | |
| task6 | CP15-NLP应用15.4-15.5 | 两天 | 3月29号、30号周四 |
Reference
[1] 动手学深度学习.李沐
[2] 动手学深度学习-文本处理
[3] 动手学深度学习-注意力机制CP10
[4] https://discuss.d2l.ai
[5] 教材:https://zh-v2.d2l.ai/
[6] 视频: https://space.bilibili.com/1567748478/channel/seriesdetail?sid=358497
[7] 笔记:https://github.com/MLNLP-World/DeepLearning-MuLi-Notes/tree/main/notes
[8] 竞赛:https://tianchi.aliyun.com/competition/entrance/231784/introduction?spm=5176.12281973.0.0.7c47106baWMBl3
[9] OpenI:https://openi.pcl.ac.cn/Datawhale/d2l