文章目录

• 1 表征共循环
• 2 一些必须的库
• 3 一个测试数据
• 4 获取用于绘制持续同伦图和共循环的参数
• 5 找到最大持续点
• 6 绘制共循环图

1 表征共循环

Ripser是基于共同伦 (cohomology) 的，它为持续共同伦算法的类生成器生成表征共循环。这里共同伦是同伦的对偶，共边界算子是边界算子的伴随算子，也就是说，共边界算子 (coboundary operator) 采用ddd形式到d+1d+1d+1形式。例如，共边界算子δ0\delta_0δ0​在向量空间 (原始边界上的函数) 采用000形式到111形式，δ1\delta_1δ1​使用111形式到222形式。一个ddd维的共循环是一个ddd形式，其δd=0\delta_d=0δd​=0。

与同伦一致，应用共边界算子两次得到零；δdδd−1=0\delta_d\delta_{d-1}=0δd​δd−1​=0，因此δd−1\delta_{d-1}δd−1​图像是δd\delta_dδd​的核，然后可以使用商Ker(δd)/Im(δd−1)Ker(\delta_d)/Im(\delta_{d-1})Ker(δd​)/Im(δd−1​)来获取共同伦组。该组中等价于mod Im(δd−1)I_m(\delta_{d-1})Im​(δd−1​)的ddd形式的特定等价类被称为共同伦类。

持续共同伦算法计算共同伦类生成器的集合，其初始和消亡讲被展示在持续图 (persistence diagram) 中。注意共同伦的初始和消亡实际上就是同伦的初始和消亡。最终可以获取表征共循环。

2 一些必须的库

import numpy as np
import matplotlib.pyplot as plt
import tadasets
from ripser import ripser
from persim import plot_diagrams

3 一个测试数据

np.random.seed(9)
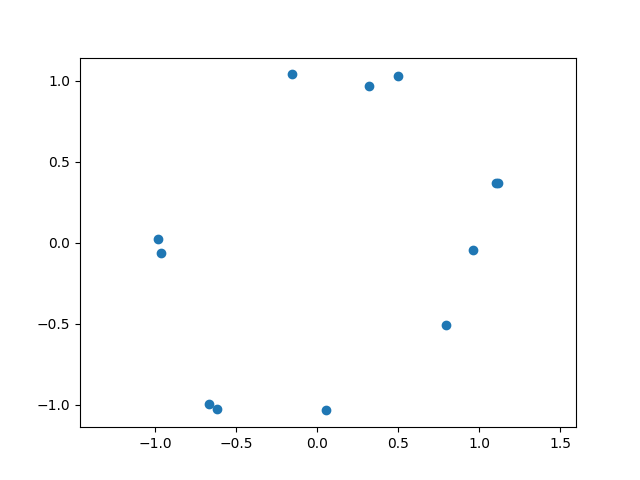
x = tadasets.dsphere(n=12, d=1, noise=0.1)plt.scatter(x[:, 0], x[:, 1])
plt.axis('equal')
plt.show()

输出如下：

4 获取用于绘制持续同伦图和共循环的参数

result = ripser(x, coeff=17, do_cocycles=True)
diagrams = result['dgms']
cocycles = result['cocycles']
D = result['dperm2all']

5 找到最大持续点

dgm1 = diagrams[1]
idx = np.argmax(dgm1[:, 1] - dgm1[:, 0])
plot_diagrams(diagrams, show = False)
plt.scatter(dgm1[idx, 0], dgm1[idx, 1], 20, 'k', 'x')
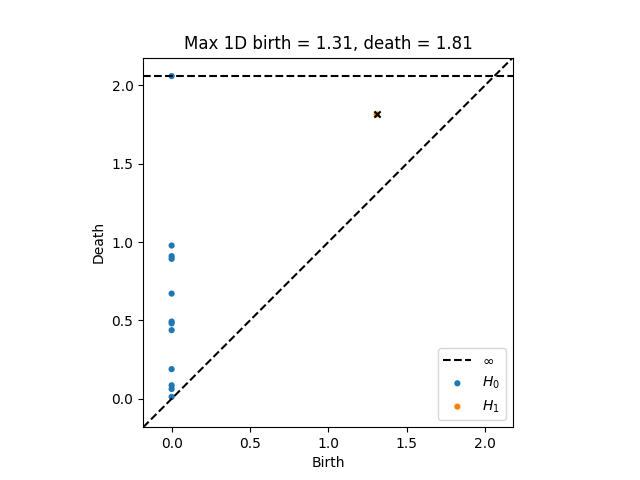
plt.title("Max 1D birth = %.3g, death = %.3g"%(dgm1[idx, 0], dgm1[idx, 1]))
plt.show()

最大持续点使用黑色×表示：

6 绘制共循环图

绘制共循环图时：

1. 展示长度小于或等于消亡时间的边；
2. 红色显示顶点的索引，蓝色显示边上的共循环值；
3. 边缘方向绘制为灰色阴影，其中边缘从黑色到白色；
4. 如果一条边没有被标记，则意味着共循环在该边上的计算结果为零。

def drawLineColored(X, C):for i in range(X.shape[0] - 1):plt.plot(X[i:i + 2, 0], X[i:i + 2, 1], c=C[i, :], lw=3)def plotCocycle2D(D, X, cocycle, thresh):"""给定2D点云X，展示投影后的共循环"""# 在阈值下绘制所有边N = X.shape[0]t = np.linspace(0, 1, 10)c = plt.get_cmap('Greys')C = c(np.array(np.round(np.linspace(0, 125, len(t))), dtype=np.int32))C = C[:, 0:3]for i in range(N):for j in range(N):if D[i, j] <= thresh:Y = np.zeros((len(t), 2))Y[:, 0] = X[i, 0] + t * (X[j, 0] - X[i, 0])Y[:, 1] = X[i, 1] + t * (X[j, 1] - X[i, 1])drawLineColored(Y, C)# 绘制共循环，即蓝色数字for k in range(cocycle.shape[0]):[i, j, val] = cocycle[k, :]if D[i, j] <= thresh:[i, j] = [min(i, j), max(i, j)]a = 0.5 * (X[i, :] + X[j, :])plt.text(a[0], a[1], '%g' % val, color='b')# 绘制顶点标签for i in range(N):plt.text(X[i, 0], X[i, 1], '%i' % i, color='r')plt.axis('equal')cocycle = cocycles[1][idx]
thresh = dgm1[idx, 1]  # 将共循环投影小于或等于消亡时间的边上
plotCocycle2D(D, x, cocycle, thresh)
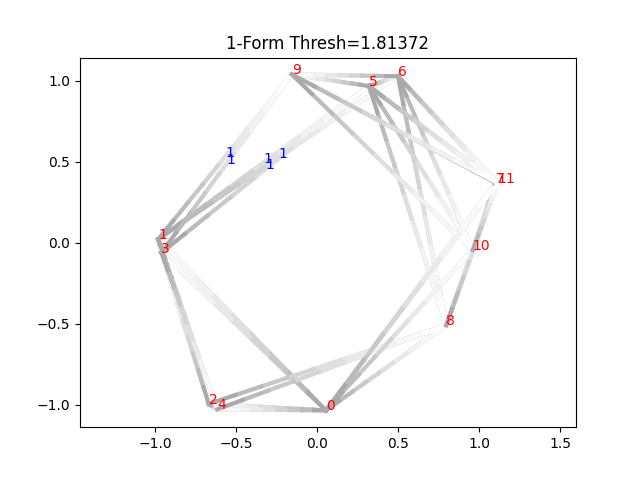
plt.title("1-Form Thresh=%g" % thresh)
plt.show()

输出如下：

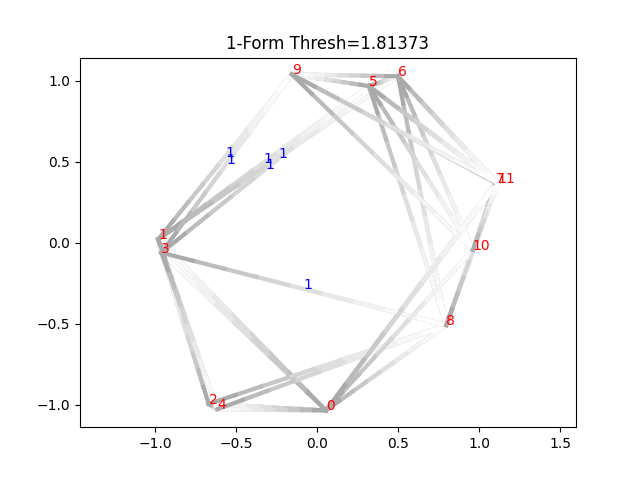
该图是一个合法的共循环图的理由是，以0、3、8作为顶点的三角形，有1+0+01 + 0 + 01+0+0，其对17取mod不为零。这是因为共循环类实际仅存在于[bi,di)[b_i,d_i)[bi​,di​)内，其中bib_ibi​和did_idi​分别是初始和消亡时间。此时如果微调一下消亡时间，也能得到一个合法的共循环：

cocycle = cocycles[1][idx]
thresh = dgm1[idx, 1] - 0.00001  # 将共循环投影小于或等于消亡时间的边上
plotCocycle2D(D, x, cocycle, thresh)
plt.title("1-Form Thresh=%g" % thresh)
plt.show()

输出如下：

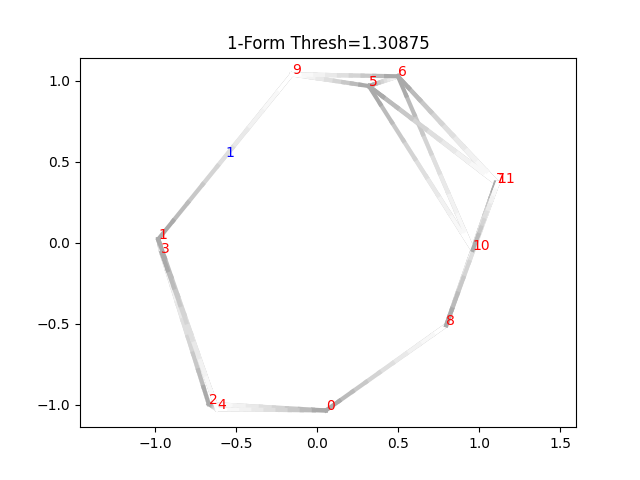
此时3与8之间的边界被去除。对于余下的三角形，也能检测其是合法的。例如，可以验证直到初始时间的所有共循环都是合法的：

cocycle = cocycles[1][idx]
thresh = dgm1[idx, 0]
plotCocycle2D(D, x, cocycle, thresh)
plt.title("1-Form Thresh=%g" % thresh)
plt.show()

输出如下：