数据结构——图
图的定义
图是由顶点的有穷非空集合和顶点之间边的集合组成的,通常表示为G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
线性表中可以没有数据元素,称为空表;树中可以没有结点,叫做空树;图的点集不能为空,边集可以为空。
各种图的定义

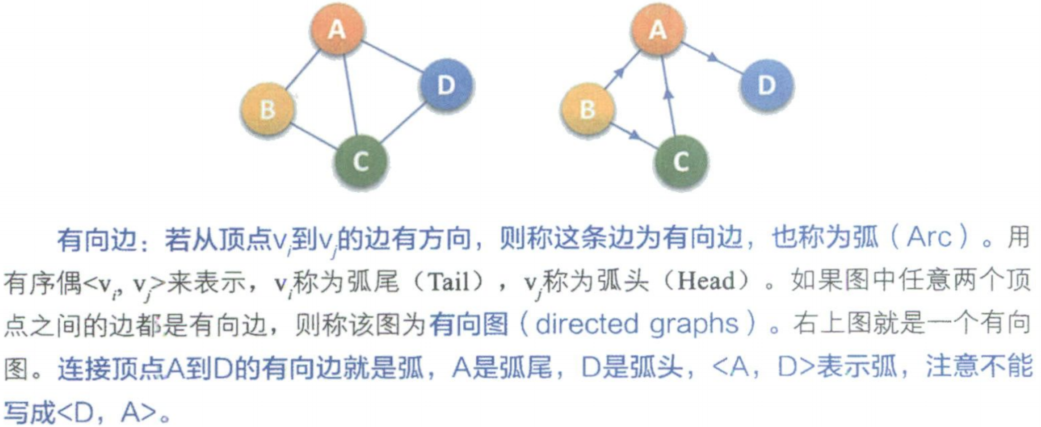

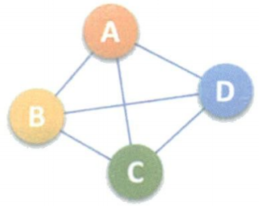

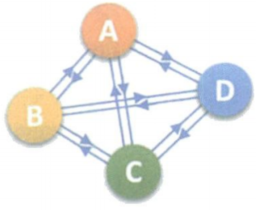
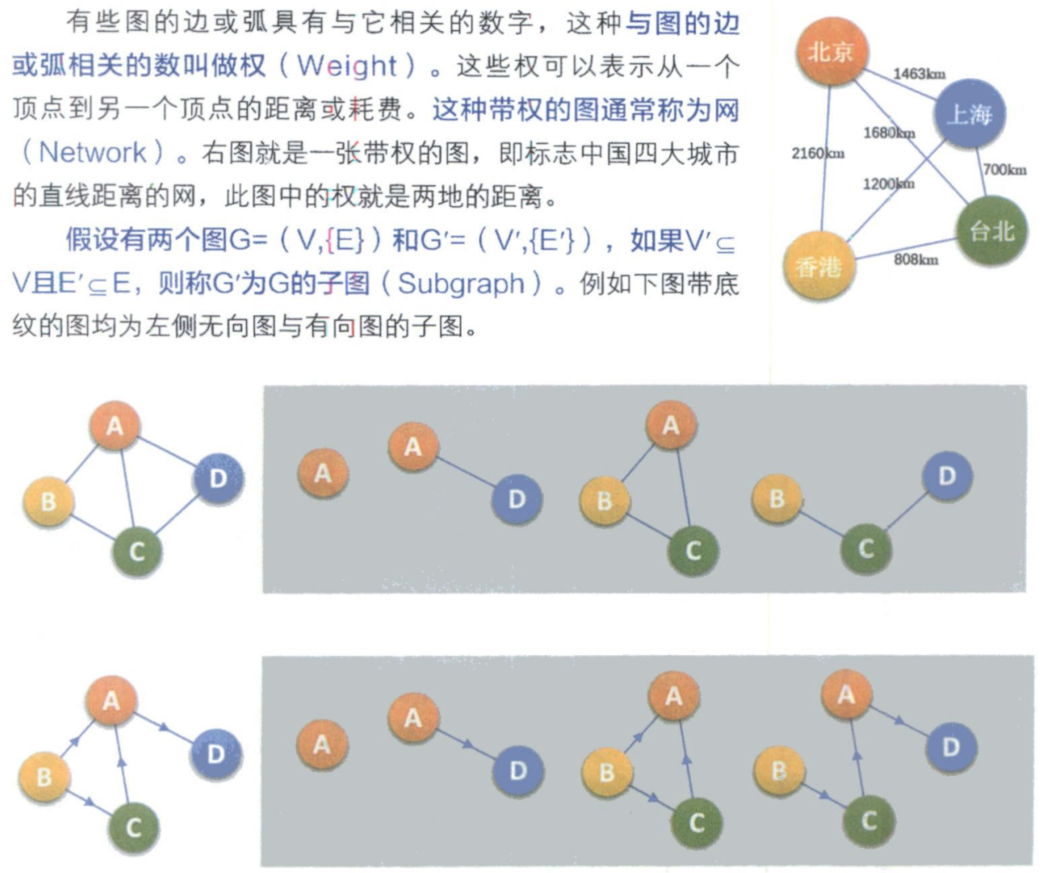
图的顶点与边间的关系


![]()
![]()

![]()
连通图的相关术语

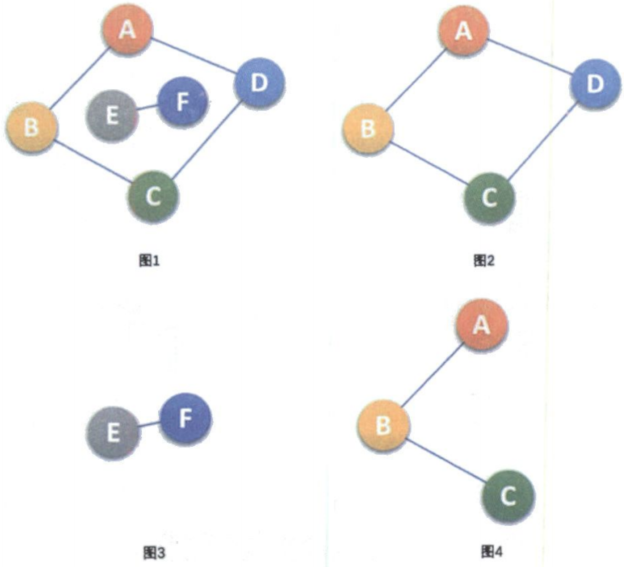

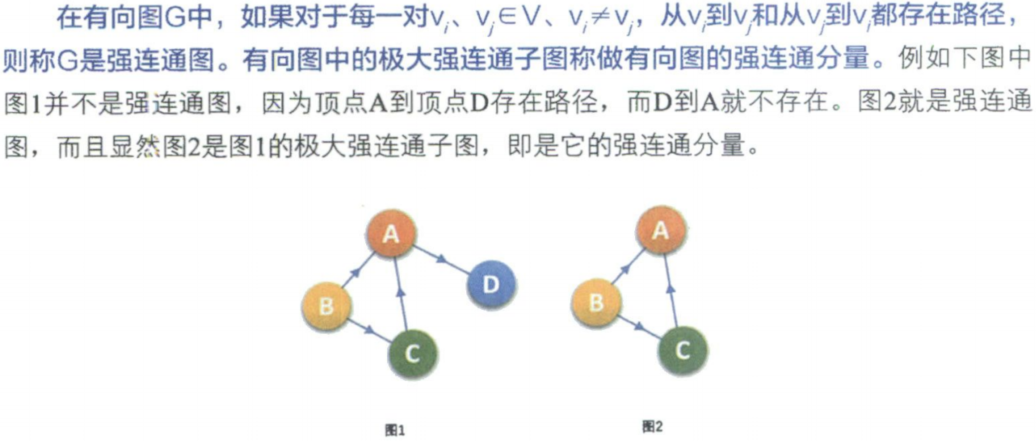
一个连通图的生成树是一个极小的连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。
图的定义与术语总结
 图的存储结构
图的存储结构
邻接矩阵
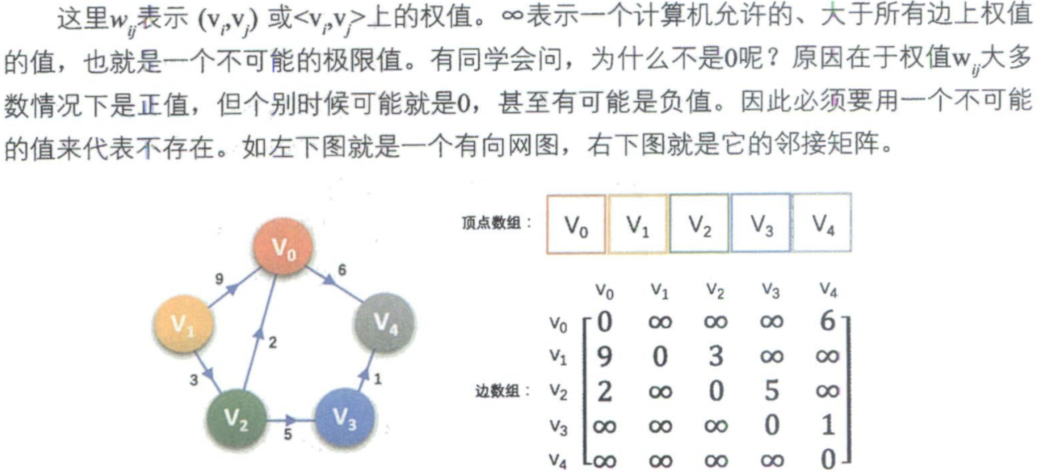
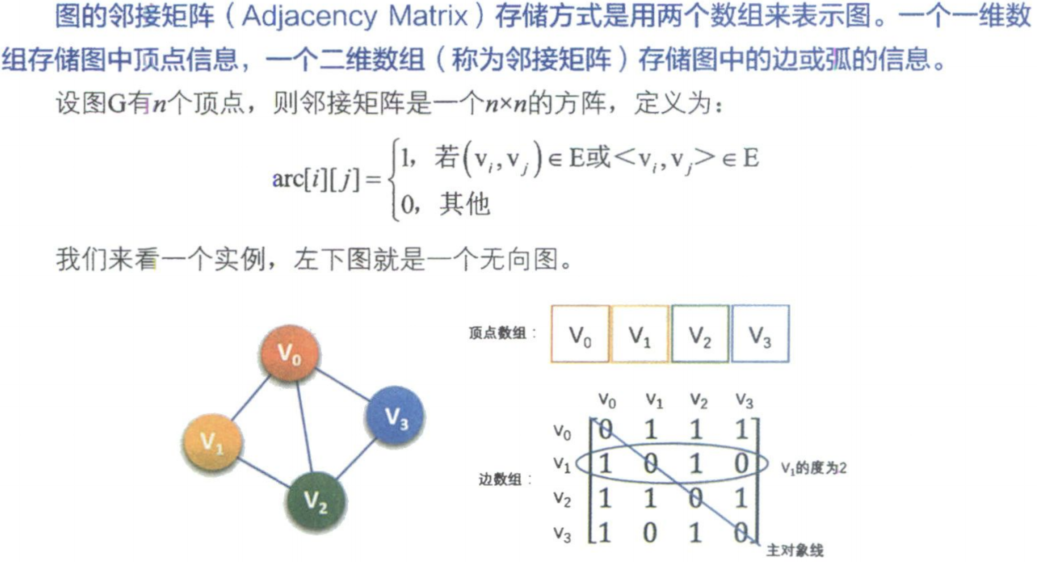 无向图的边数组是一个对称矩阵。
无向图的边数组是一个对称矩阵。
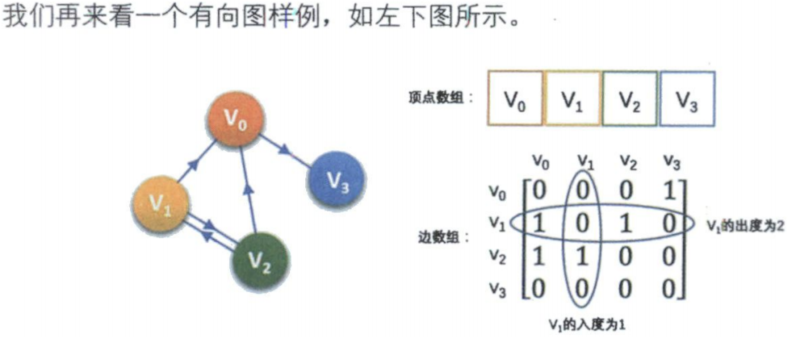


typedef char VertexType; /* 顶点类型应由用户定义 */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */
#define MAXVEX 100 /* 最大顶点数,应由用户定义 */
#define INFINITY 65535 /* 用65535来代表∞ */
typedef struct
{VertexType vexs[MAXVEX]; /* 顶点表 */EdgeType arc[MAXVEX][MAXVEX]; /* 邻接矩阵,可看作边表 */int numNodes, numEdges; /* 图中当前的顶点数和边数 */
}MGraph;/* 建立无向网图的邻接矩阵表示 */
void CreateMGraph(MGraph *G)
{int i,j,k,w;printf("输入顶点数和边数:\n");scanf("%d,%d",&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */for(i = 0;i numNodes;i++) /* 读入顶点信息,建立顶点表 */scanf(&G->vexs[i]);for(i = 0;i numNodes;i++)for(j = 0;j numNodes;j++)G->arc[i][j]=INFINITY; /* 邻接矩阵初始化 */for(k = 0;k numEdges;k++) /* 读入numEdges条边,建立邻接矩阵 */{printf("输入边(vi,vj)上的下标i,下标j和权w:\n");scanf("%d,%d,%d",&i,&j,&w); /* 输入边(vi,vj)上的权w */G->arc[i][j]=w; G->arc[j][i]= G->arc[i][j]; /* 因为是无向图,矩阵对称 */}
} 邻接表
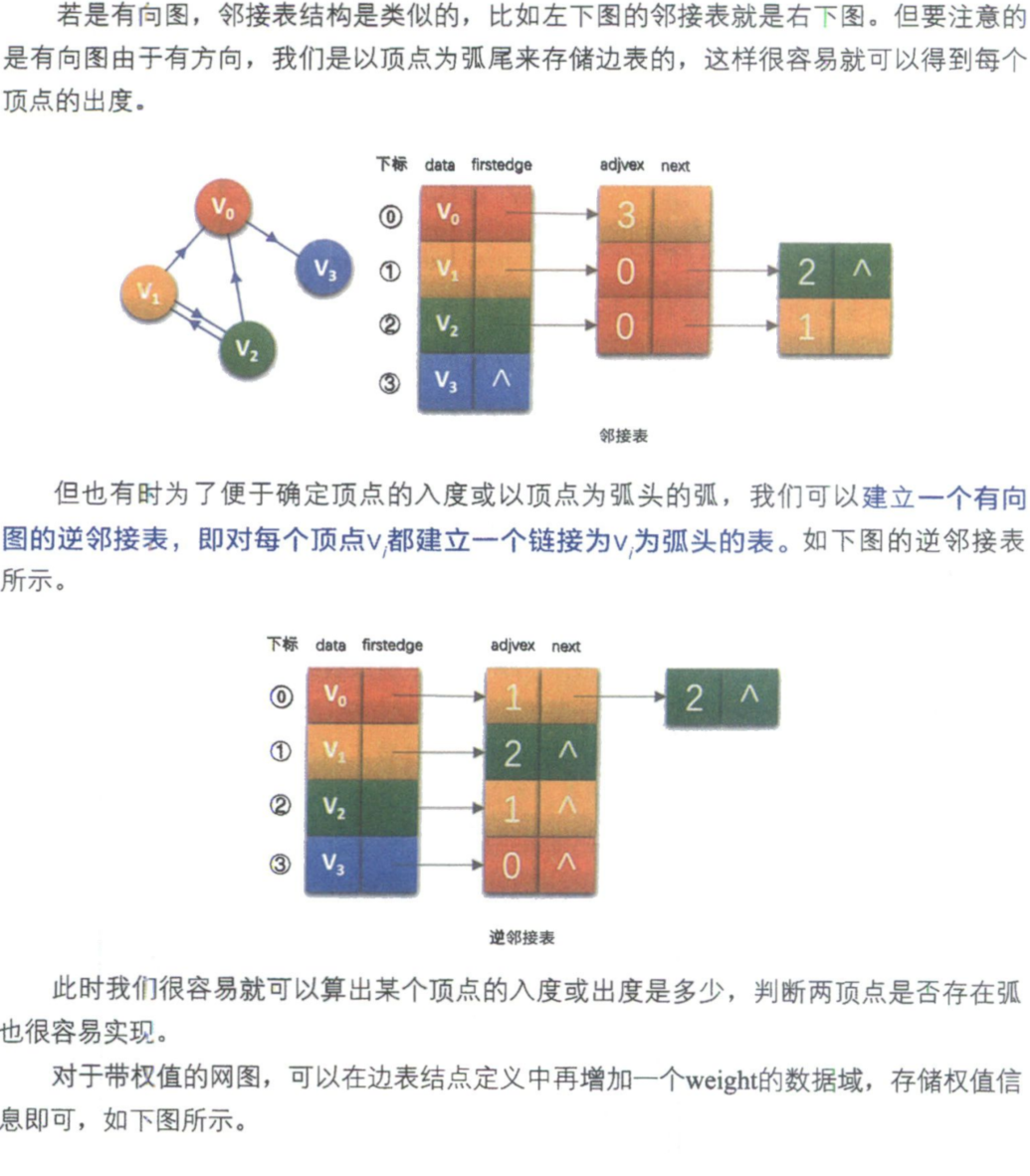
邻接矩阵是不错的一种图存储结构,但是我们也发现,对于边数相对顶点较少的图,这种结构是存在对存储空间的极大浪费的。
将数组与链表相结合的存储方法称为邻接表。



typedef char VertexType; /* 顶点类型应由用户定义 */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */typedef struct EdgeNode /* 边表结点 */
{int adjvex; /* 邻接点域,存储该顶点对应的下标 */EdgeType info; /* 用于存储权值,对于非网图可以不需要 */struct EdgeNode *next; /* 链域,指向下一个邻接点 */
}EdgeNode;typedef struct VertexNode /* 顶点表结点 */
{VertexType data; /* 顶点域,存储顶点信息 */EdgeNode *firstedge; /* 边表头指针 */
}VertexNode, AdjList[MAXVEX];typedef struct
{AdjList adjList; int numNodes,numEdges; /* 图中当前顶点数和边数 */
}GraphAdjList;无向图的邻接表的创建代码如下
/* 建立图的邻接表结构 */
void CreateALGraph(GraphAdjList *G)
{int i,j,k;EdgeNode *e;printf("输入顶点数和边数:\n");scanf("%d,%d",&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */for(i = 0;i < G->numNodes;i++) /* 读入顶点信息,建立顶点表 */{scanf(&G->adjList[i].data); /* 输入顶点信息 */G->adjList[i].firstedge=NULL; /* 将边表置为空表 */}for(k = 0;k < G->numEdges;k++) /* 建立边表 */{printf("输入边(vi,vj)上的顶点序号:\n");scanf("%d,%d",&i,&j); /* 输入边(vi,vj)上的顶点序号 */ e=(EdgeNode *)malloc(sizeof(EdgeNode)); /* 向内存申请空间,生成边表结点 */ e->adjvex=j; /* 邻接序号为j */ e->next=G->adjList[i].firstedge; /* 将e的指针指向当前顶点上指向的结点 */G->adjList[i].firstedge=e; /* 将当前顶点的指针指向e */ e=(EdgeNode *)malloc(sizeof(EdgeNode)); /* 向内存申请空间,生成边表结点 */ e->adjvex=i; /* 邻接序号为i */ e->next=G->adjList[j].firstedge; /* 将e的指针指向当前顶点上指向的结点 */G->adjList[j].firstedge=e; /* 将当前顶点的指针指向e */ }
}对于无向图,一条边都是对应两个顶点,所以在循环中,一次就针对i和j分别进行了插入。本算法的时间复杂度,对于n个顶点e条边来说,很容易得出是O(n+e)。
十字链表

![]()


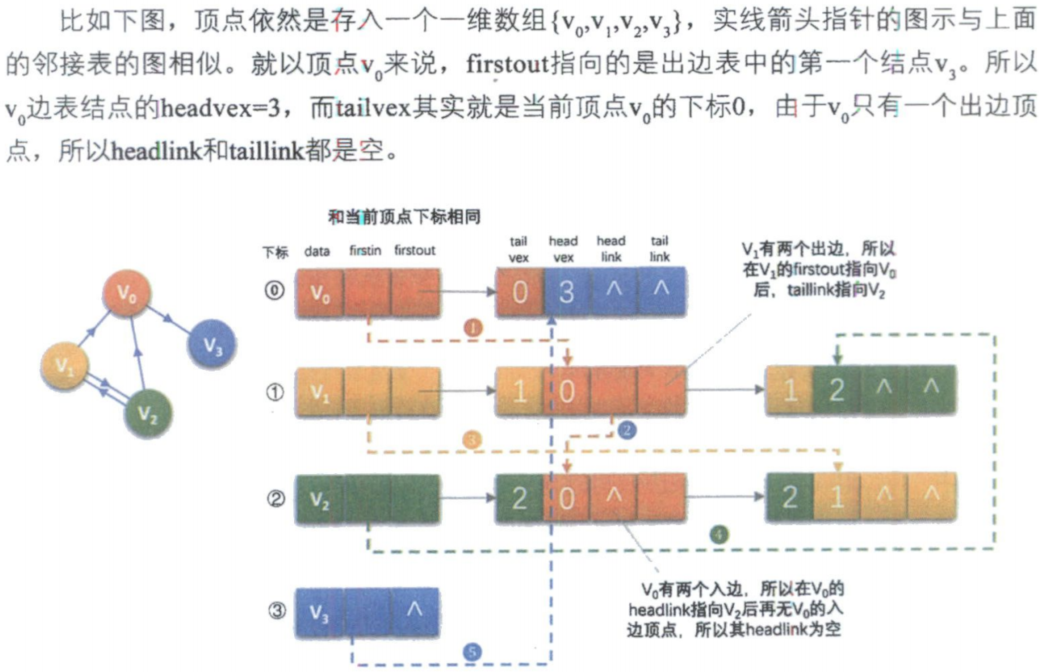

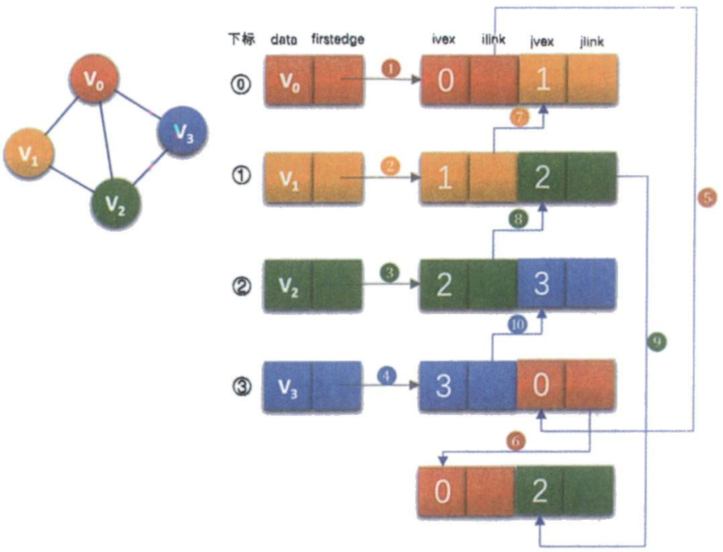
邻接多重表
 有4个顶点5条边,先将4个顶点和5条边表结点画出来,然后再连线。
有4个顶点5条边,先将4个顶点和5条边表结点画出来,然后再连线。
 边集数组
边集数组
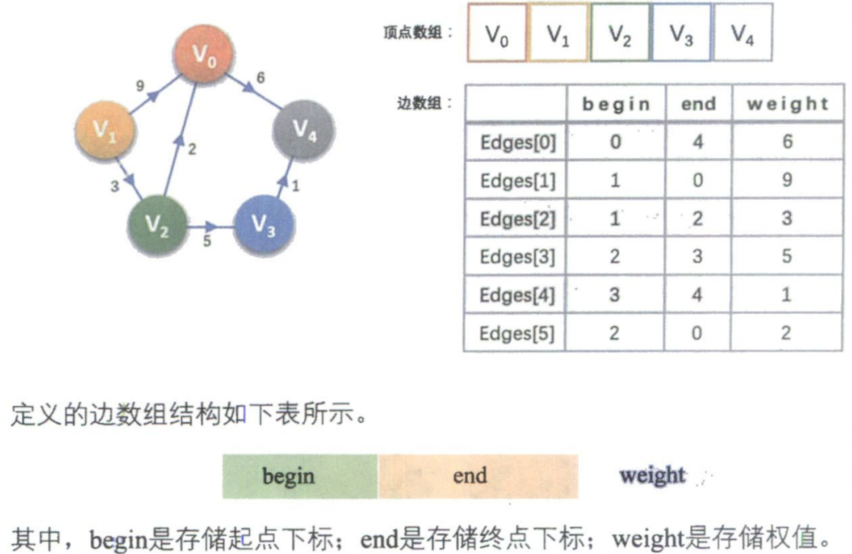
图的遍历
从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程就叫做图的遍历。
图极有可能存在沿着某条路径搜索后,又回到原顶点,而有些顶点却还没有遍历到的情况。因此我们需要在遍历过程中把访问过的顶点打上标记,以避免访问多次而不自知。具体办法是设置一个访问数组visited[n],n是图中顶点的个数,初值为0,访问后设置为1。
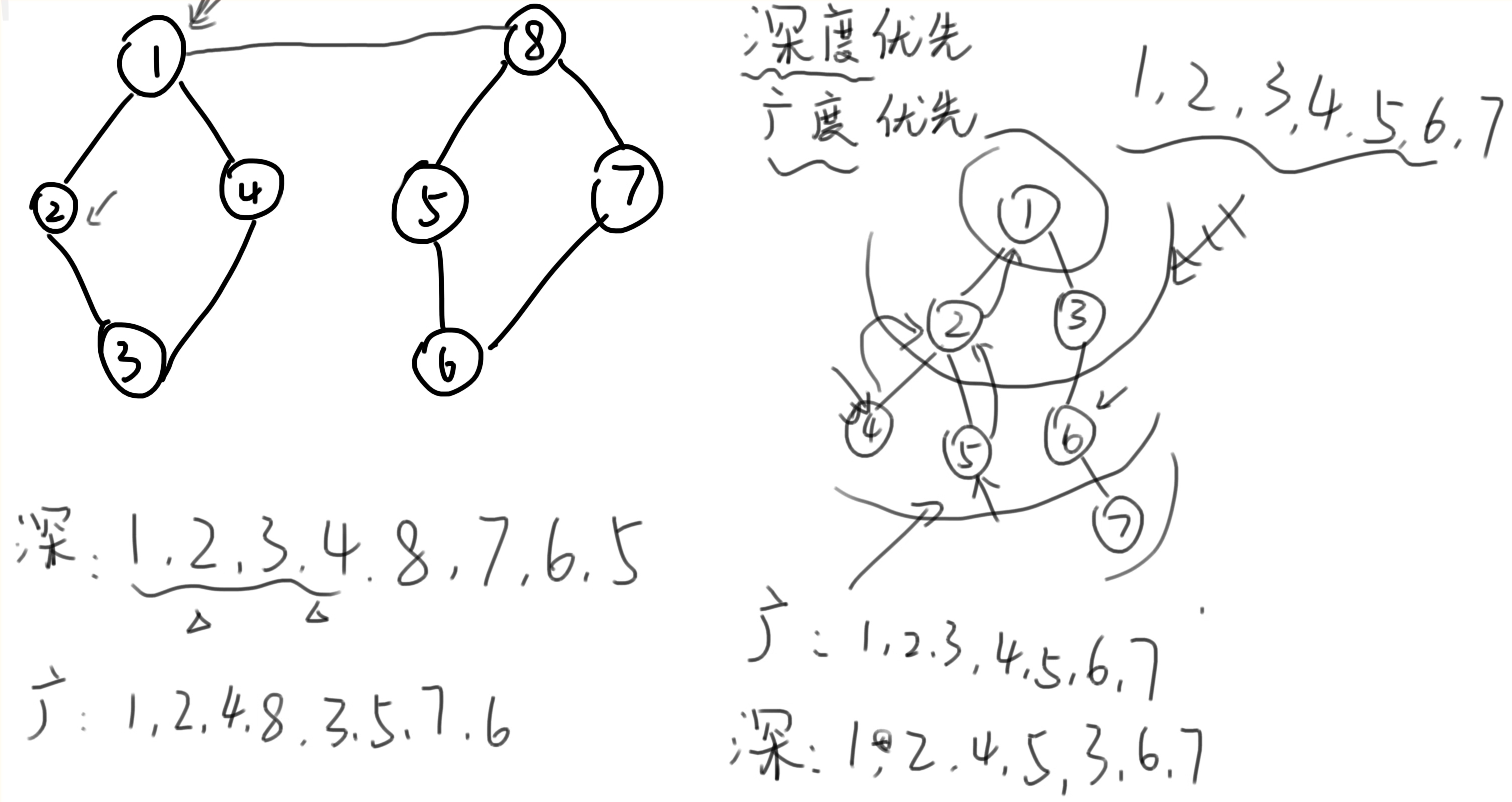
深度优先遍历
图的深度优先遍历与树的先序遍历类似,即尽可能深的遍历图。
如果我们用的是邻接矩阵的方式,则代码如下
#define MAXVEX 9
Boolean visited[MAXVEX]; /* 访问标志的数组 *//* 邻接矩阵的深度优先递归算法 */
void DFS(MGraph G, int i)
{int j;visited[i] = TRUE; /*该顶点已被访问*/printf("%c ", G.vexs[i]); /* 打印顶点,也可以其它操作 */for(j = 0; j < G.numVertexes; j++)if(G.arc[i][j] == 1 && !visited[j])DFS(G, j); /* 对未访问的邻接顶点递归调用 */
}/* 邻接矩阵的深度遍历操作 */
//从每个顶点进行深度优先遍历,防止非连通图
void DFSTraverse(MGraph G)
{int i;for(i = 0; i < G.numVertexes; i++)visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */for(i = 0; i < G.numVertexes; i++)if(!visited[i]) /* 对未访问过的顶点调用DFS,若连通图仅执行一次 */ DFS(G, i);
}如果图结构是邻接表结构,其DFSTraverse函数的代码是几乎相同的,只是在递归函数中因为将数组换成了链表而有所不同
/* 邻接表的深度优先递归算法 */
void DFS(GraphAdjList GL, int i)
{EdgeNode *p;visited[i] = TRUE;printf("%c ",GL->adjList[i].data); /* 打印顶点,也可以其它操作 */p = GL->adjList[i].firstedge;while(p){if(!visited[p->adjvex])DFS(GL, p->adjvex); /* 对为访问的邻接顶点递归调用 */p = p->next;}
}/* 邻接表的深度遍历操作 */
void DFSTraverse(GraphAdjList GL)
{int i;for(i = 0; i < GL->numVertexes; i++)visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */for(i = 0; i < GL->numVertexes; i++)if(!visited[i]) /* 对未访问过的顶点调用DFS,若是连通图,只会执行一次 */ DFS(GL, i);
}
 广度优先遍历
广度优先遍历
图的广度优先遍历与树的层次遍历类似,需要借助队列来实现
基本思想:
- 首先访问某一顶点v,并由v出发,依次访问顶点v未被访问过的所有邻接顶点w1,w2…wi;
- 再依次访问w1,w2…wi未被访问过的所有邻接顶点;
- 重复上述过程,直到所有顶点被访问;
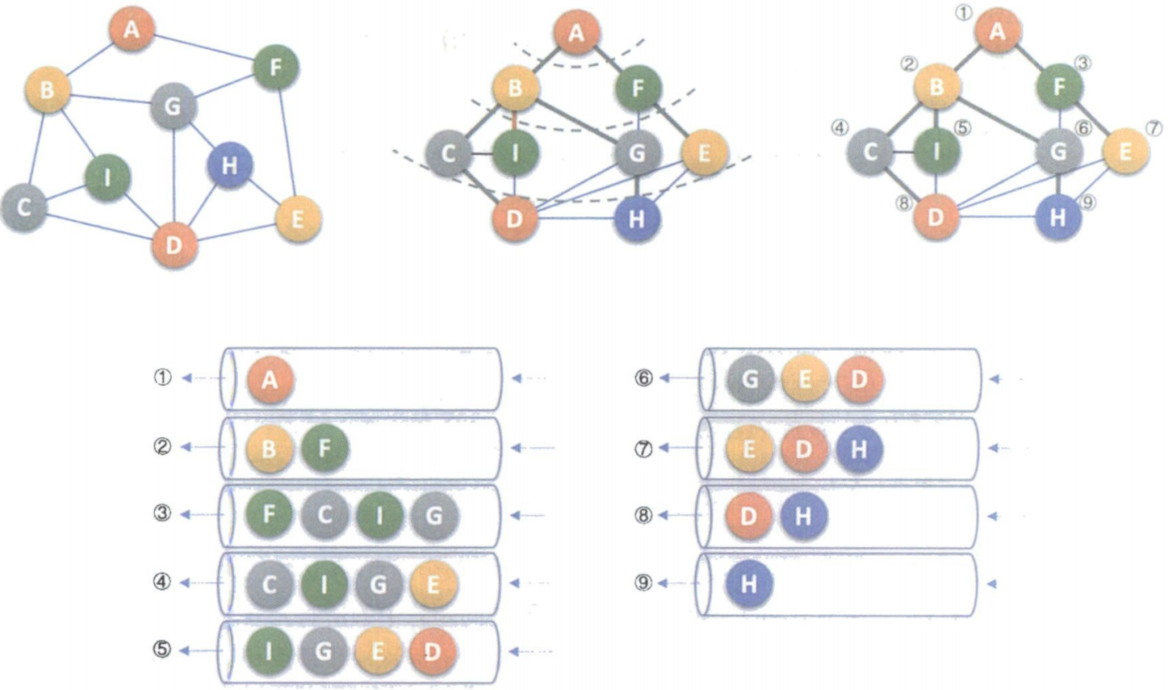
邻接矩阵的广度优先遍历算法:
/* 邻接矩阵的广度遍历算法 */
void BFSTraverse(MGraph G)
{int i, j;Queue Q;for(i = 0; i < G.numVertexes; i++)visited[i] = FALSE;InitQueue(&Q); /* 初始化一辅助用的队列 */for(i = 0; i < G.numVertexes; i++) /* 对每一个顶点做循环 */{if (!visited[i]) /* 若是未访问过就处理 */{visited[i]=TRUE; /* 设置当前顶点访问过 */printf("%c ", G.vexs[i]); /* 打印顶点,也可以其它操作 */EnQueue(&Q,i); /* 将此顶点入队列 */while(!QueueEmpty(Q)) /* 若当前队列不为空 */{DeQueue(&Q,&i); /* 将队对元素出队列,赋值给i */for(j=0;j邻接表的广度优先遍历算法
/* 邻接表的广度遍历算法 */
void BFSTraverse(GraphAdjList GL)
{int i;EdgeNode *p;Queue Q;for(i = 0; i < GL->numVertexes; i++)visited[i] = FALSE;InitQueue(&Q);for(i = 0; i < GL->numVertexes; i++){if (!visited[i]){visited[i]=TRUE;printf("%c ",GL->adjList[i].data); /* 打印顶点,也可以其它操作 */EnQueue(&Q,i);while(!QueueEmpty(Q)){DeQueue(&Q,&i);p = GL->adjList[i].firstedge; /* 找到当前顶点的边表链表头指针 */while(p){if(!visited[p->adjvex]) /* 若此顶点未被访问 */{visited[p->adjvex]=TRUE;printf("%c ",GL->adjList[p->adjvex].data);EnQueue(&Q,p->adjvex); /* 将此顶点入队列 */}p = p->next; /* 指针指向下一个邻接点 */}}}}
}
最小生成树
我们把构造连通网的最小代价生成树称为最小生成树。
普里姆(Prim)算法
就是在每次加入时每次将之前加入的顶点看作一个整体,再选择一个整体外的路径最短的顶点加入。
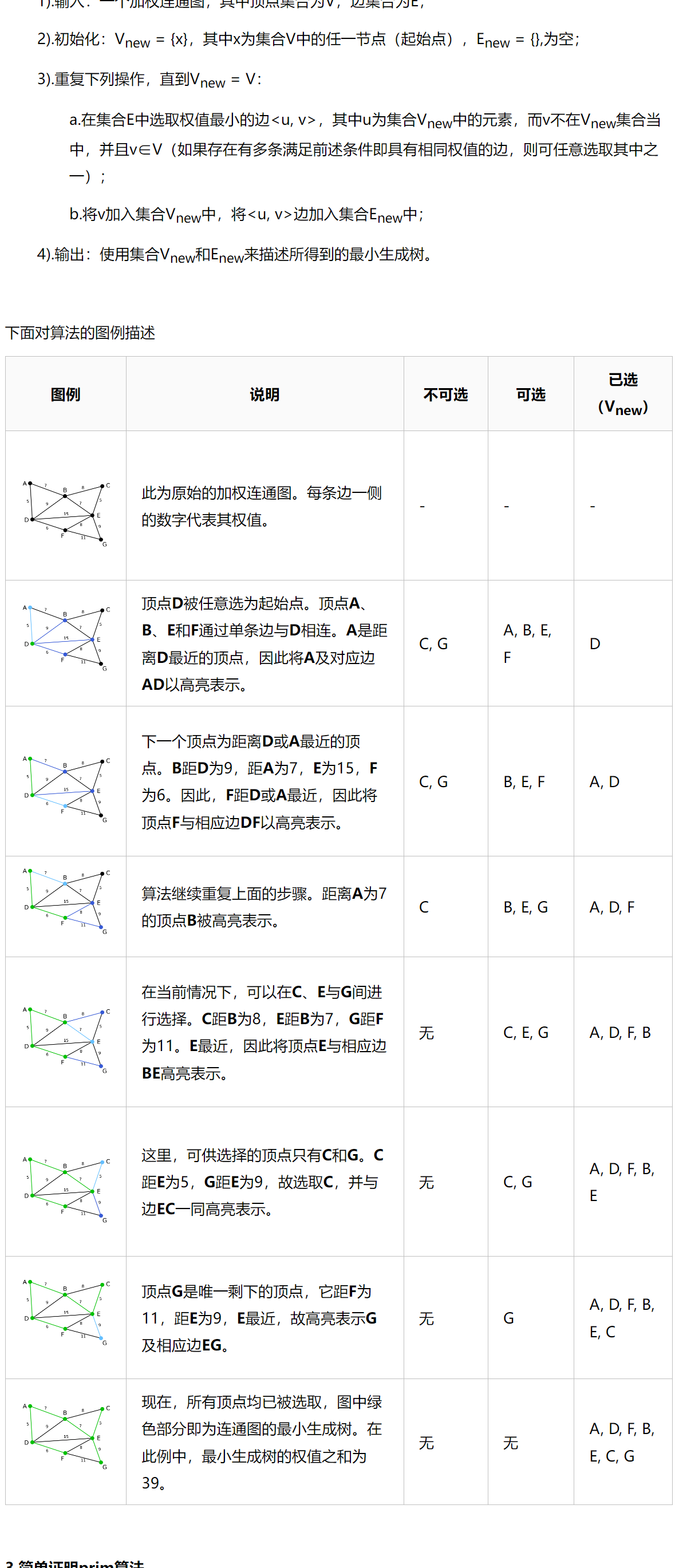
/* Prim算法生成最小生成树 */
void MiniSpanTree_Prim(MGraph G)
{int min, i, j, k;int adjvex[MAXVEX]; /* 保存相关顶点下标 */int lowcost[MAXVEX]; /* 保存相关顶点间边的权值 */lowcost[0] = 0;/* 初始化第一个权值为0,即v0加入生成树 *//* lowcost的值为0,在这里就是此下标的顶点已经加入生成树 */adjvex[0] = 0; /* 初始化第一个顶点下标为0 */for(i = 1; i < G.numVertexes; i++) /* 循环除下标为0外的全部顶点 */{lowcost[i] = G.arc[0][i]; /* 将v0顶点与之有边的权值存入数组 */adjvex[i] = 0; /* 初始化都为v0的下标 */}for(i = 1; i < G.numVertexes; i++){min = GRAPH_INFINITY; /* 初始化最小权值为∞, *//* 通常设置为不可能的大数字如32767、65535等 */j = 1;k = 0;while(j < G.numVertexes) /* 循环全部顶点 */{if(lowcost[j]!=0 && lowcost[j] < min)/* 如果权值不为0且权值小于min */{ min = lowcost[j]; /* 则让当前权值成为最小值 */k = j; /* 将当前最小值的下标存入k */}j++;}printf("(%d, %d)\n", adjvex[k], k);/* 打印当前顶点边中权值最小的边 */lowcost[k] = 0;/* 将当前顶点的权值设置为0,表示此顶点已经完成任务 */for(j = 1; j < G.numVertexes; j++) /* 循环所有顶点 */{if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j]) {/* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */lowcost[j] = G.arc[k][j];/* 将较小的权值存入lowcost相应位置 */adjvex[j] = k; /* 将下标为k的顶点存入adjvex */}}}
}克鲁斯卡尔(Kruskal)算法
直接去找最小权值的边来构建生成树也是很自然的想法,只不过构建时要考虑是否会形成环路。
typedef struct
{int begin;int end;int weight;
}Edge; /* 对边集数组Edge结构的定义 */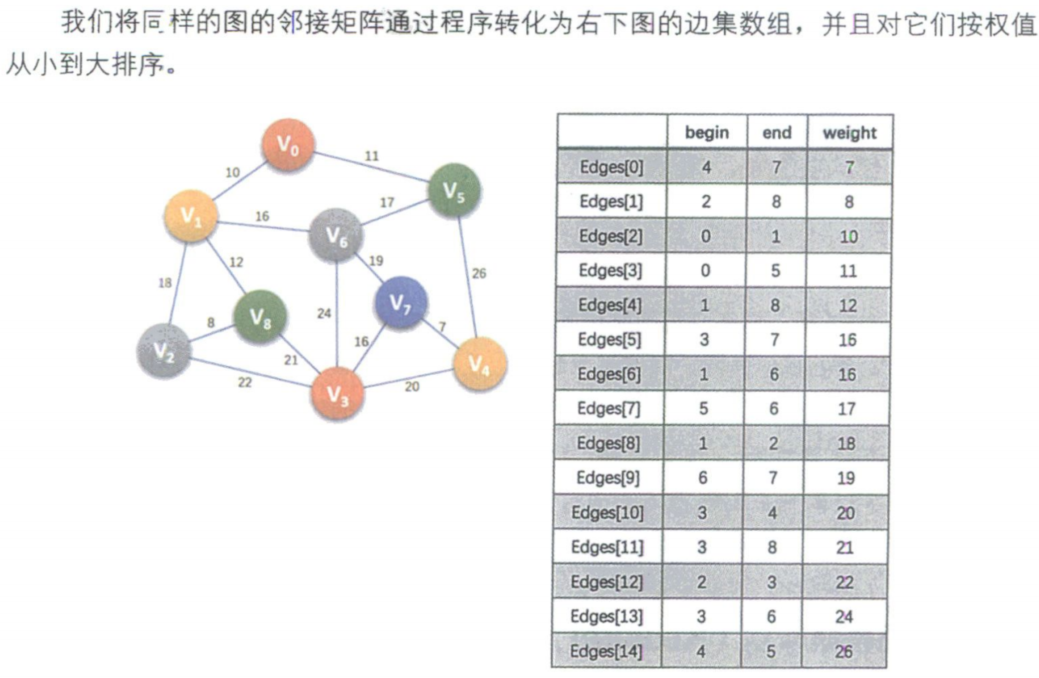
从小到大每次取出一条边添加到图中,如果形成了环,就抛弃这条边,直到选中n-1条边为止。
/* 查找连线顶点的尾部下标 */
int Find(int *parent, int f)
{while ( parent[f] > 0){f = parent[f];}return f;
}/* 生成最小生成树 */
void MiniSpanTree_Kruskal(MGraph G)
{int i, j, n, m;int k = 0;int parent[MAXVEX];/* 定义一数组用来判断边与边是否形成环路 */Edge edges[MAXEDGE];/* 定义边集数组,edge的结构为begin,end,weight,均为整型 *//* 用来构建边集数组并排序********************* */for ( i = 0; i < G.numVertexes-1; i++){for (j = i + 1; j < G.numVertexes; j++){if (G.arc[i][j]最短路径

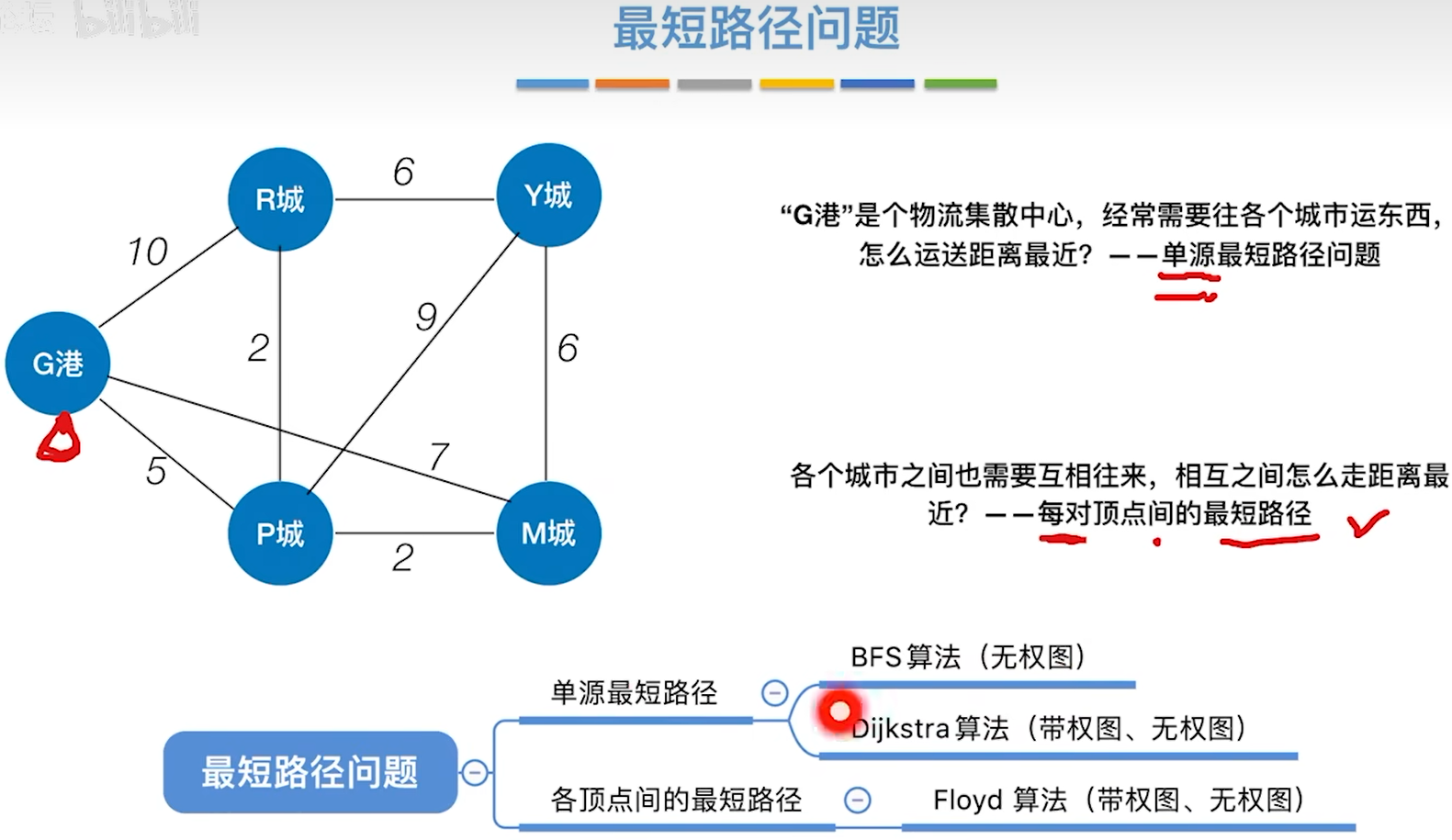
BFS算法
相当于对广度优先算法进行了改造。
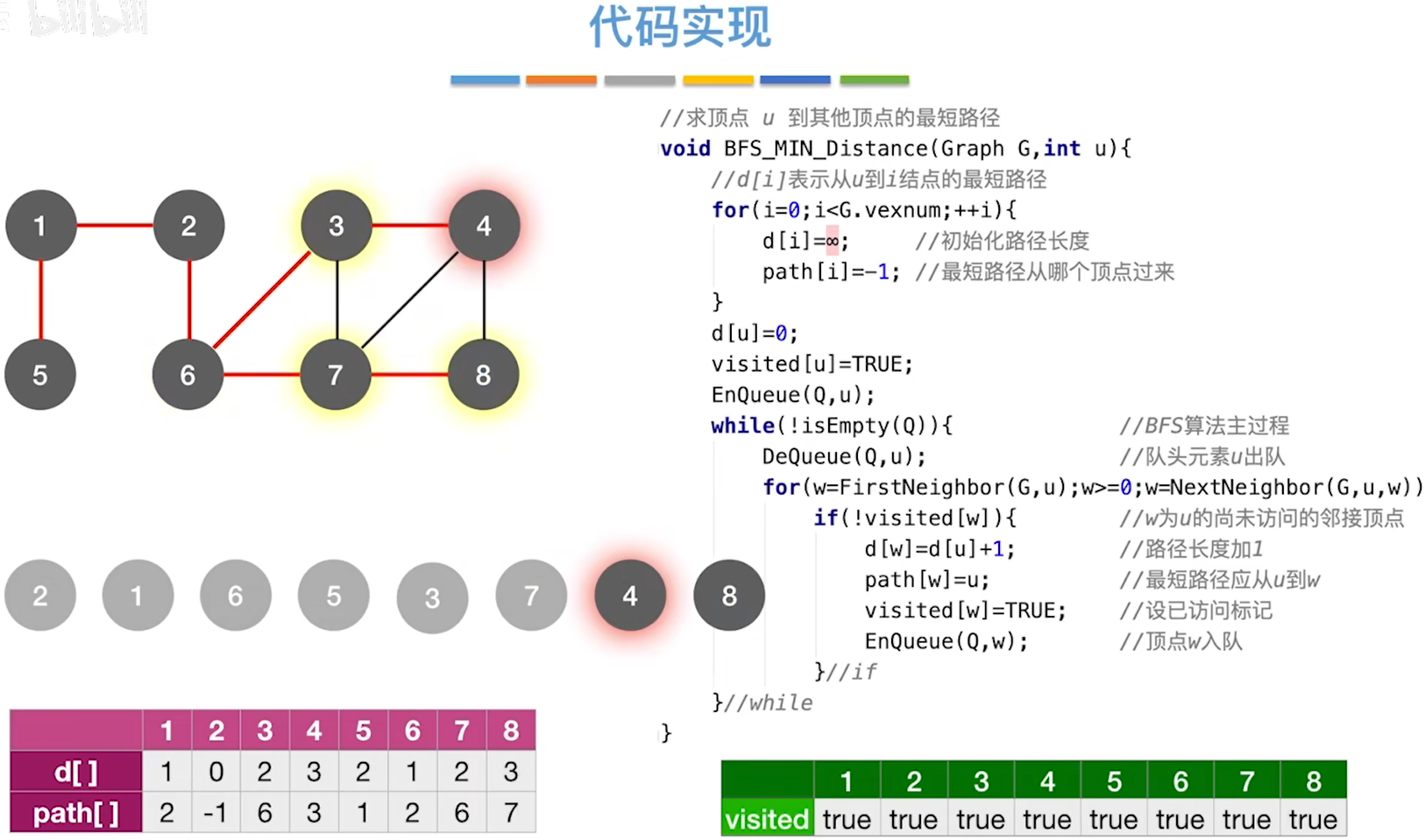

Dijkstra算法
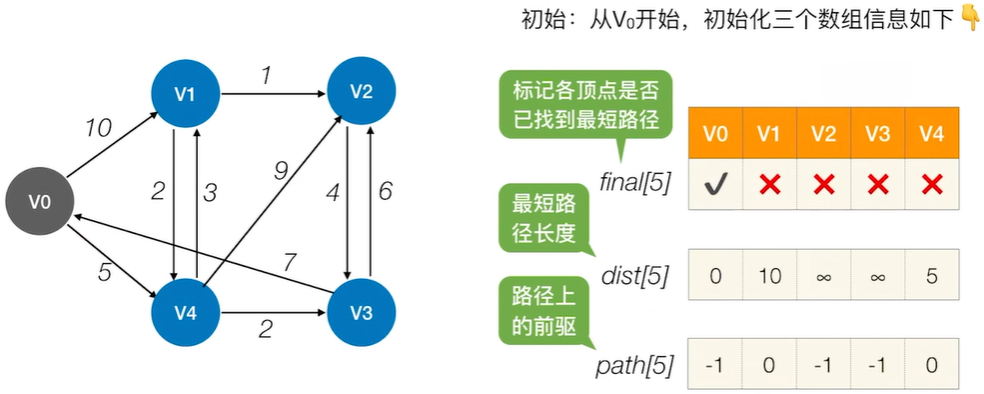
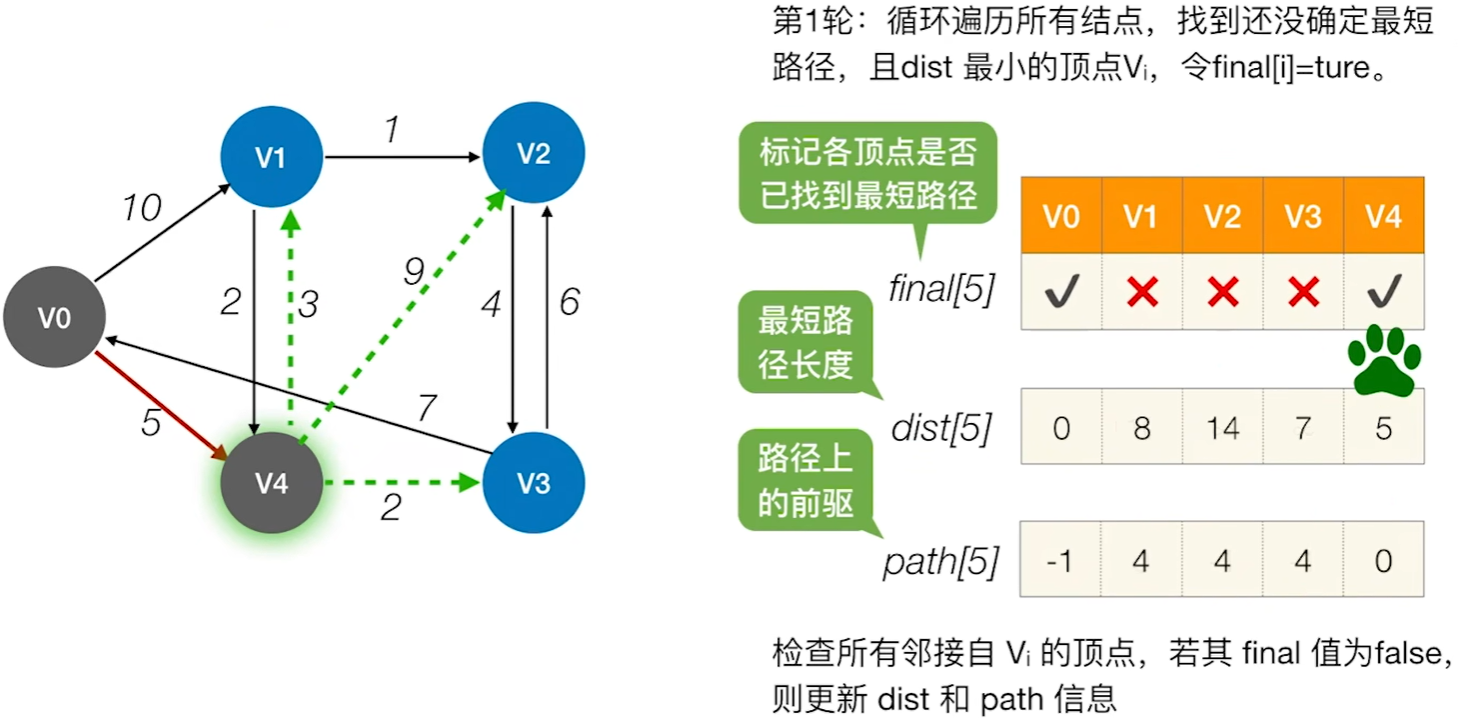
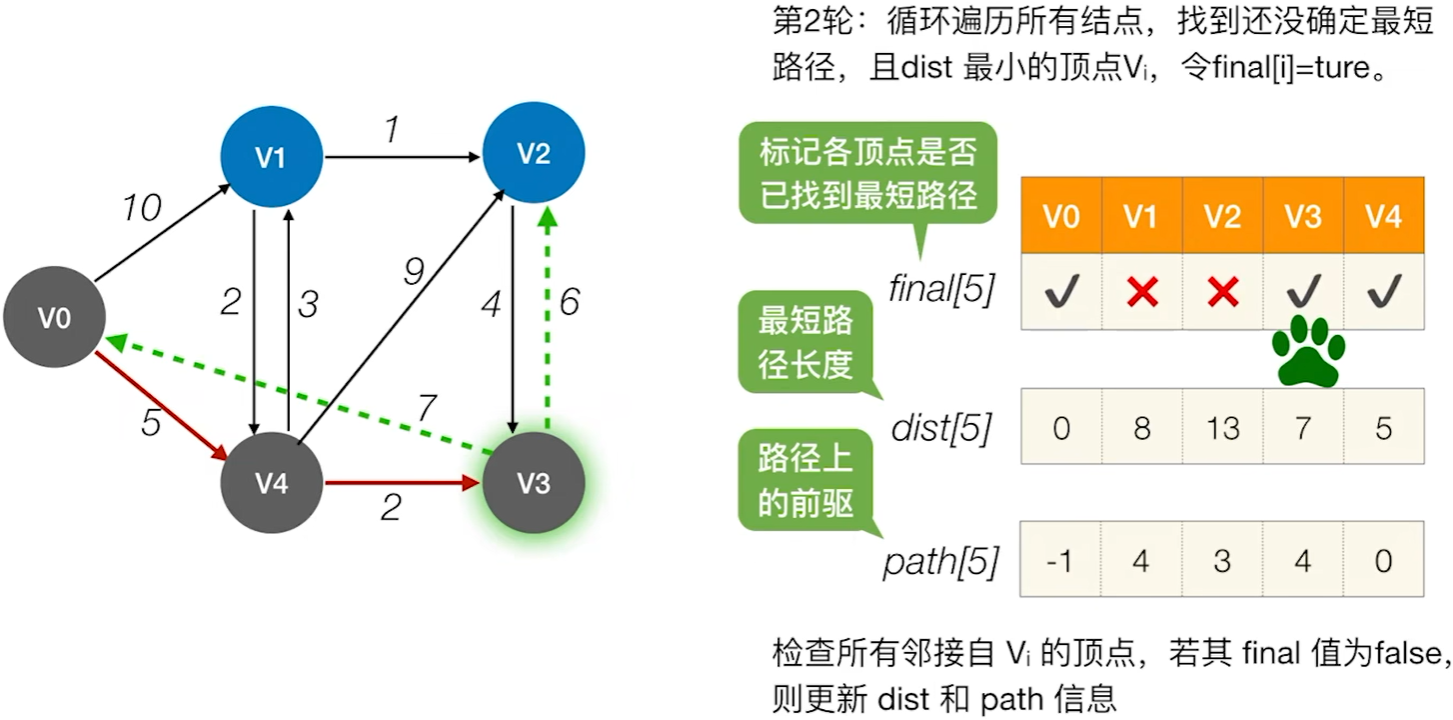
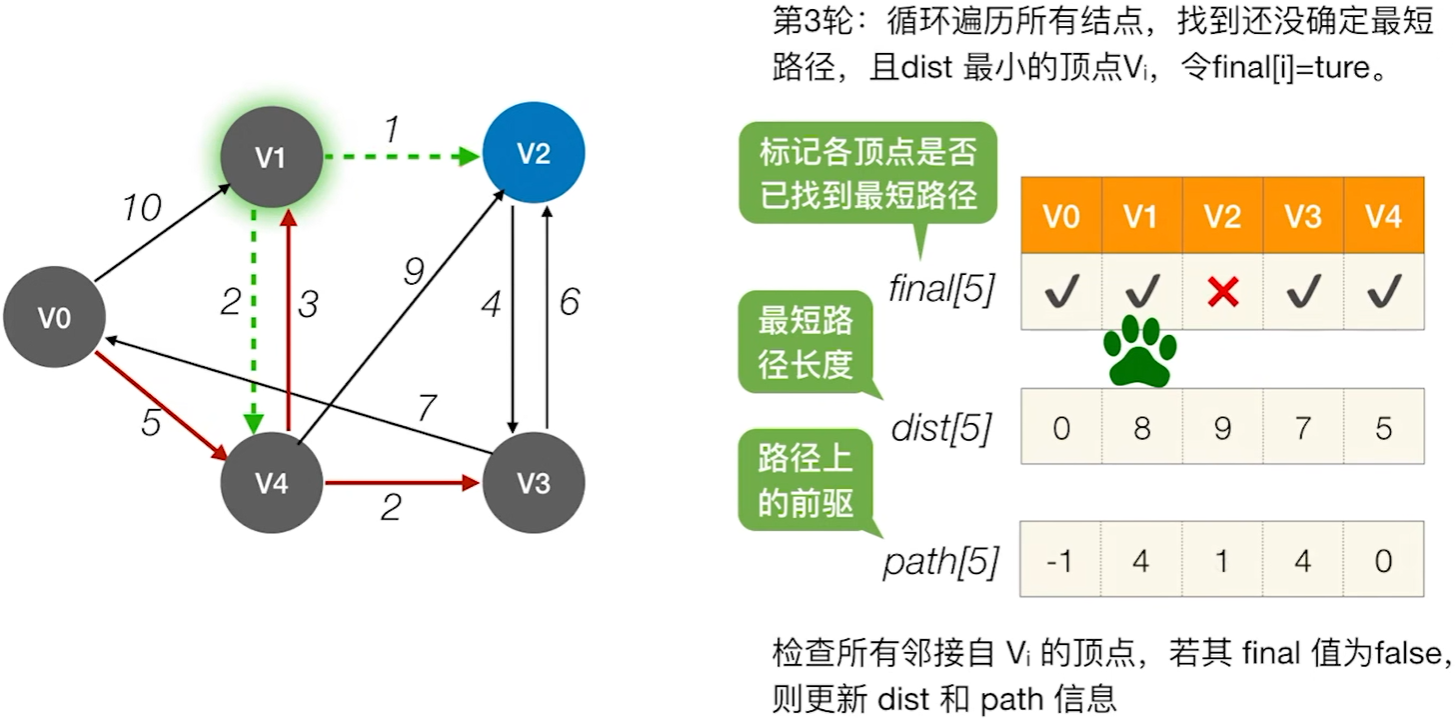
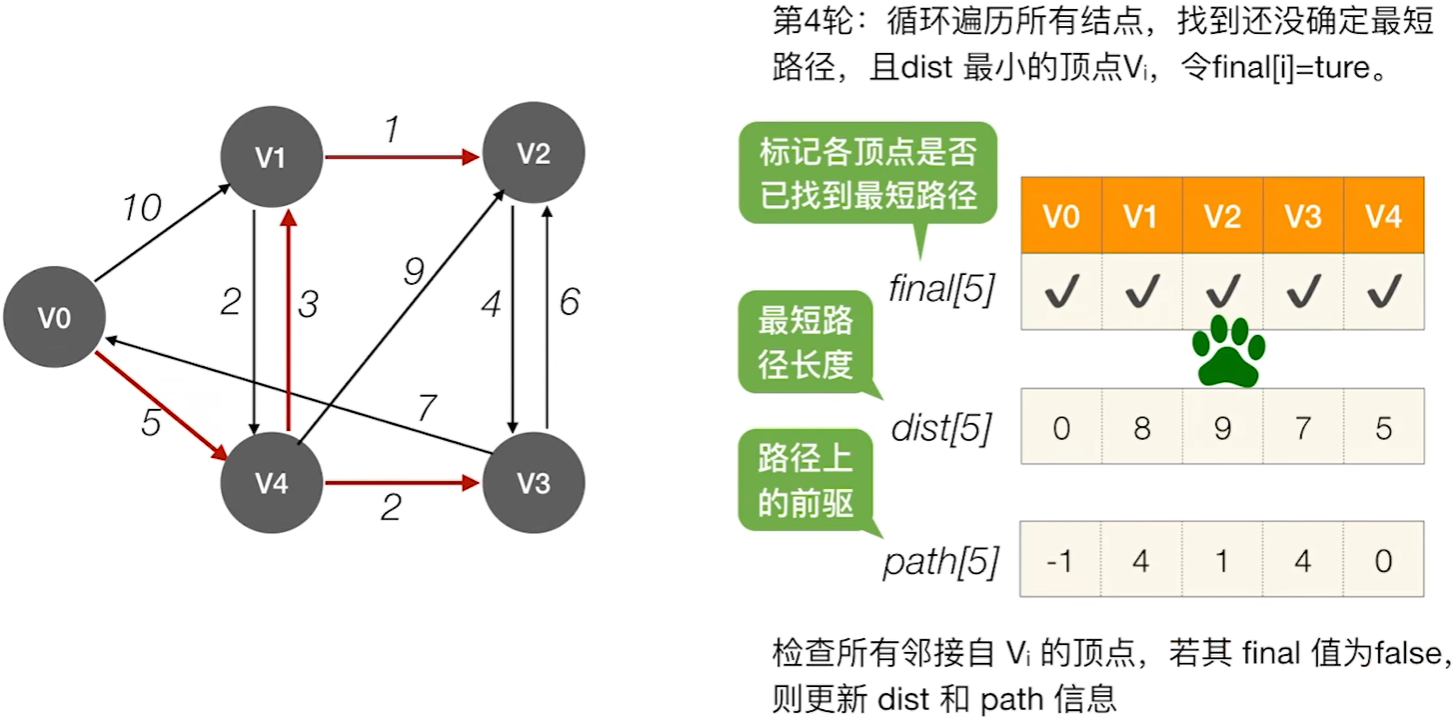
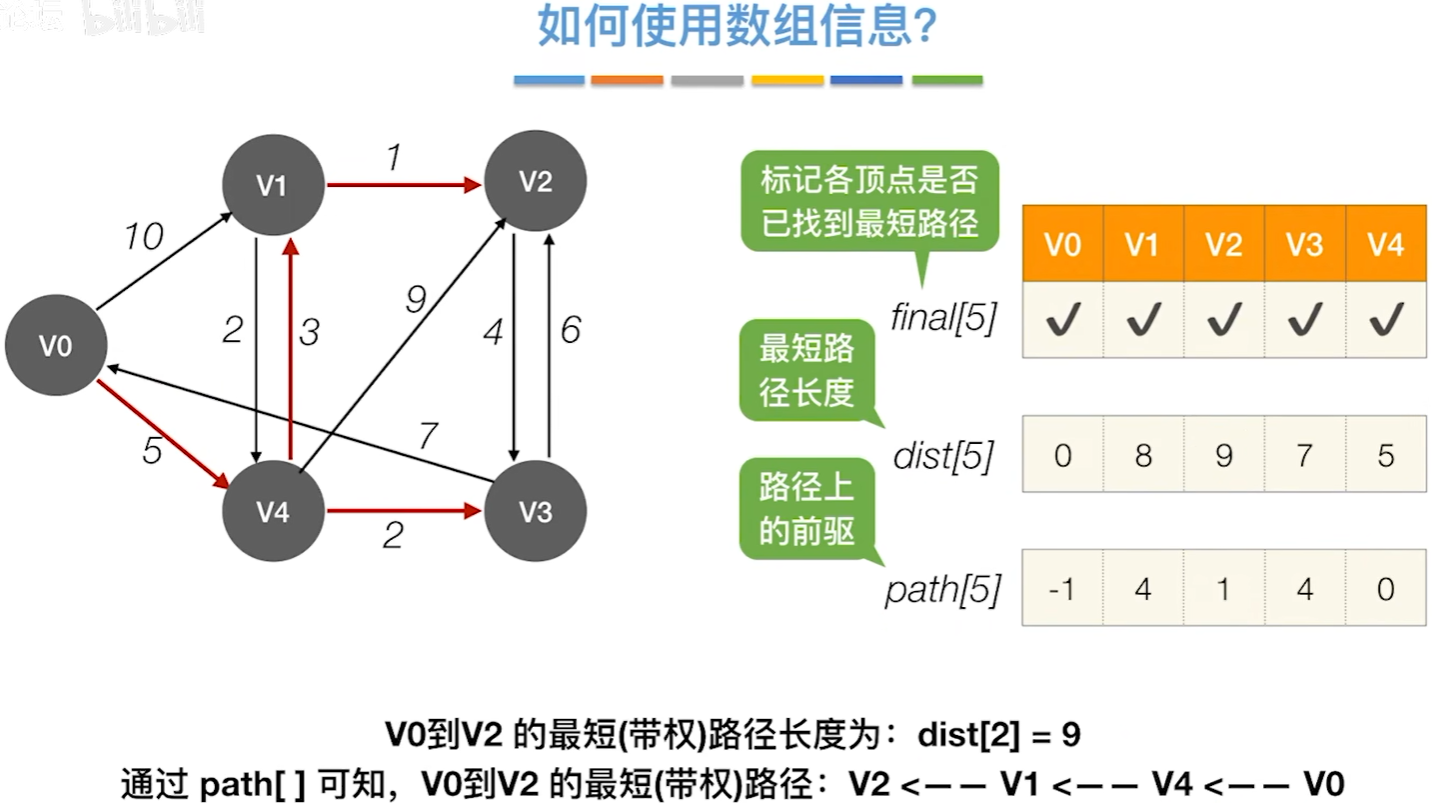
typedef struct
{int vexs[MAXVEX];int arc[MAXVEX][MAXVEX];int numVertexes, numEdges;
}MGraph;typedef int Patharc[MAXVEX]; /* 用于存储最短路径下标的数组 */
typedef int ShortPathTable[MAXVEX];/* 用于存储到各点最短路径的权值和 *//* Dijkstra算法,求有向网G的v0顶点到其余顶点v的最短路径P[v]及带权长度D[v] */
/* P[v]的值为前驱顶点下标,D[v]表示v0到v的最短路径长度和 */
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc *P, ShortPathTable *D)
{ int v,w,k,min; int final[MAXVEX];/* final[w]=1表示求得顶点v0至vw的最短路径 */for(v=0; v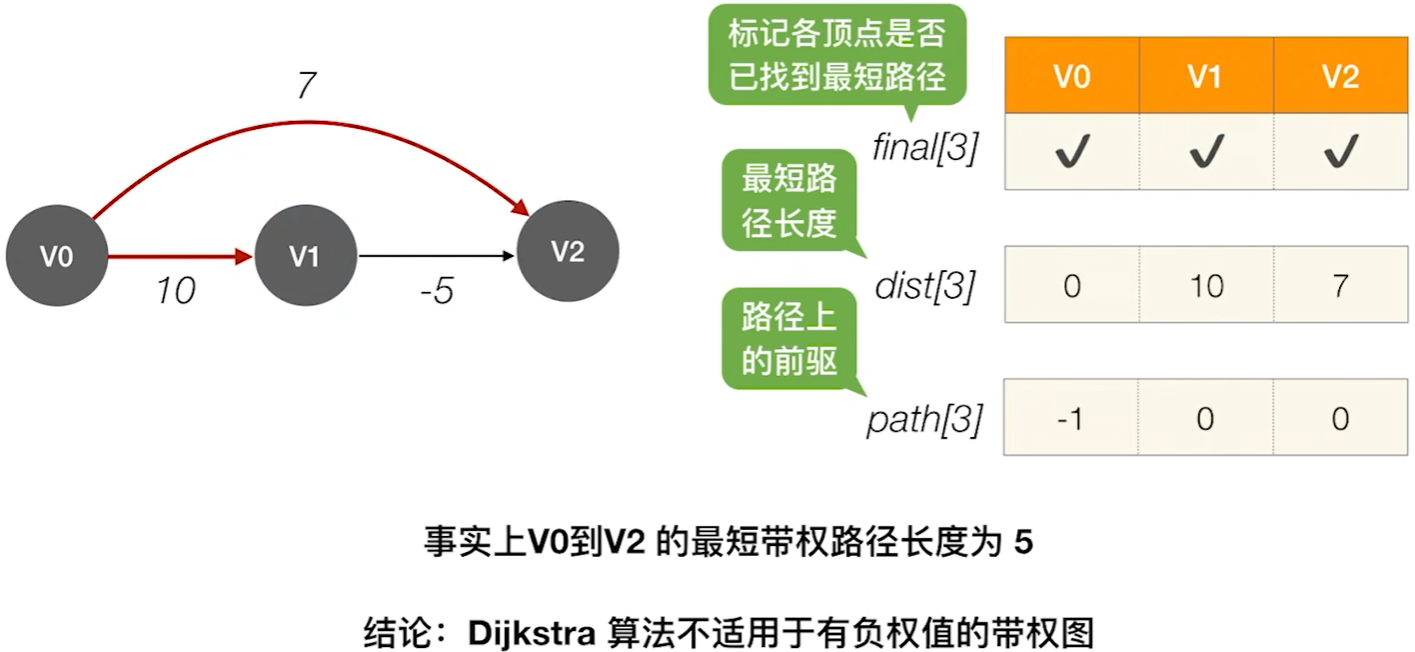
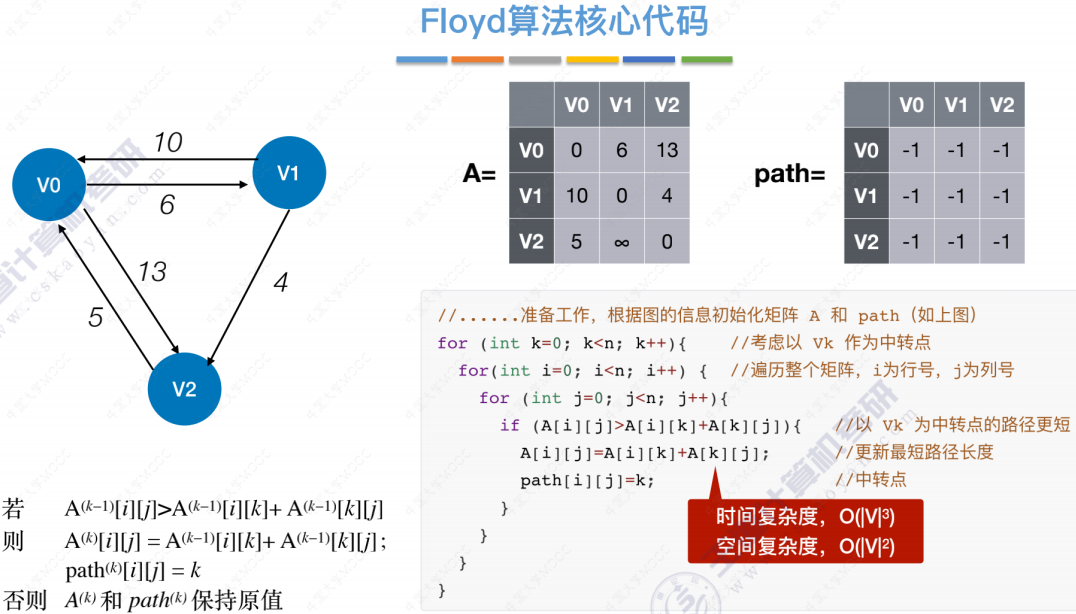
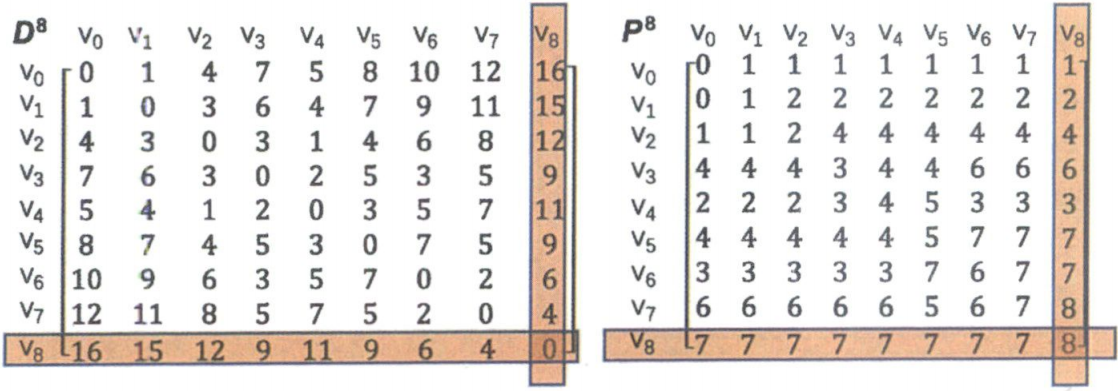
Floyd算法

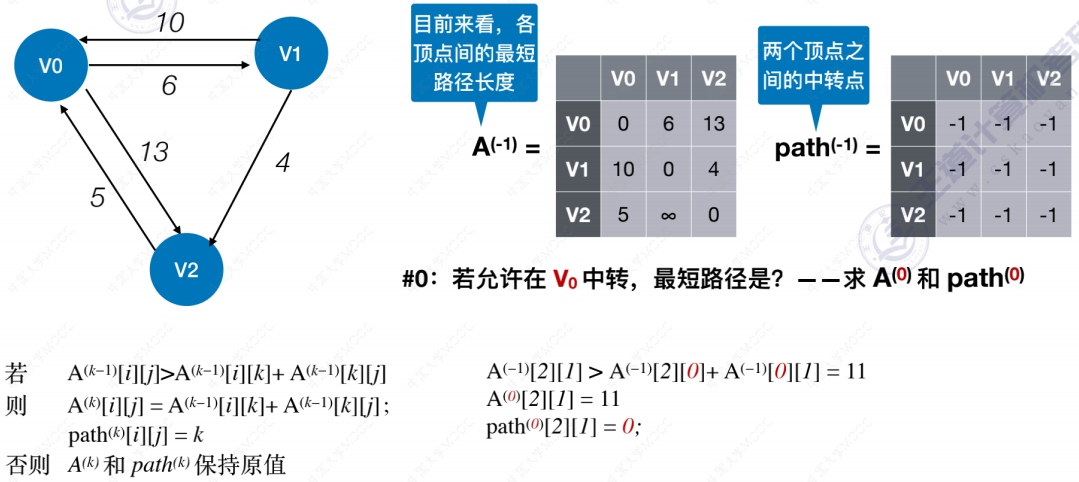
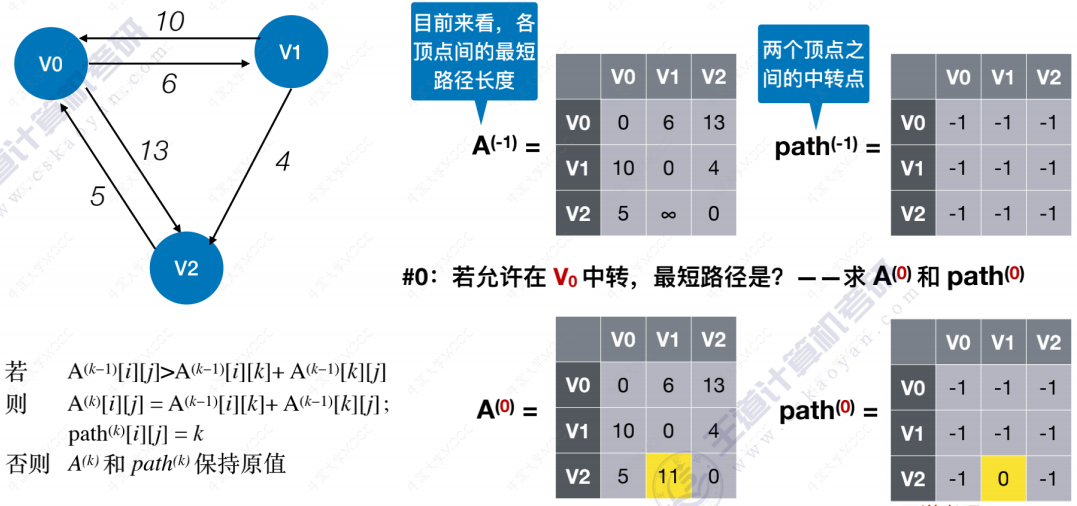
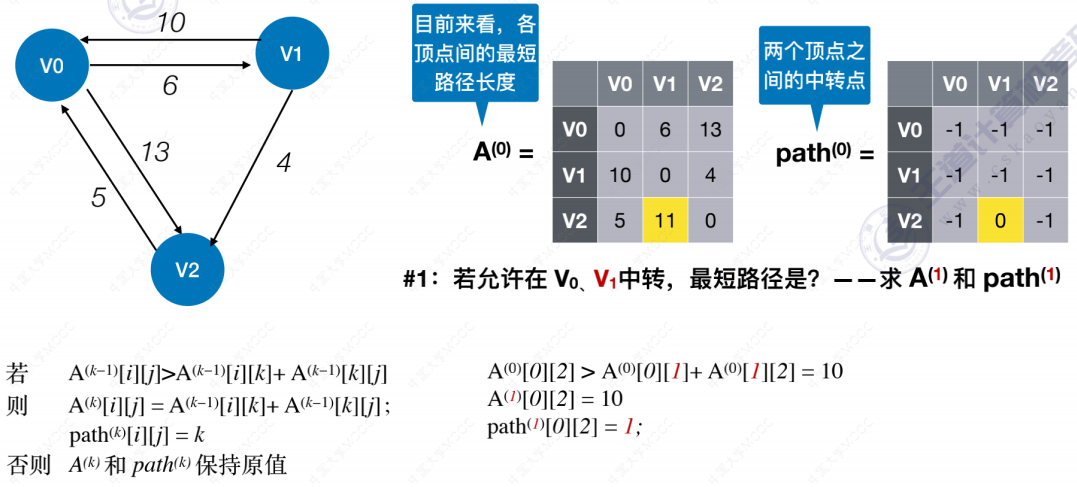
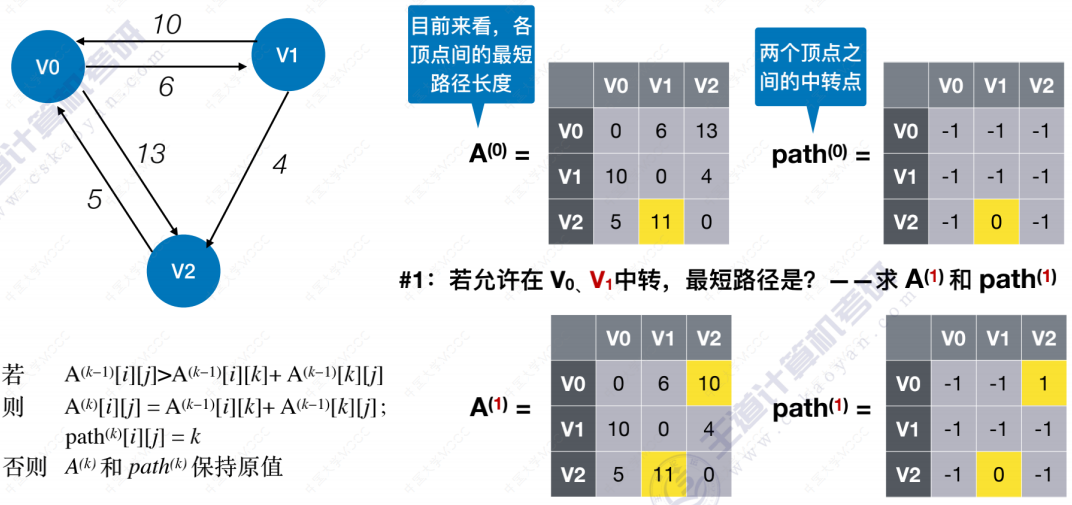
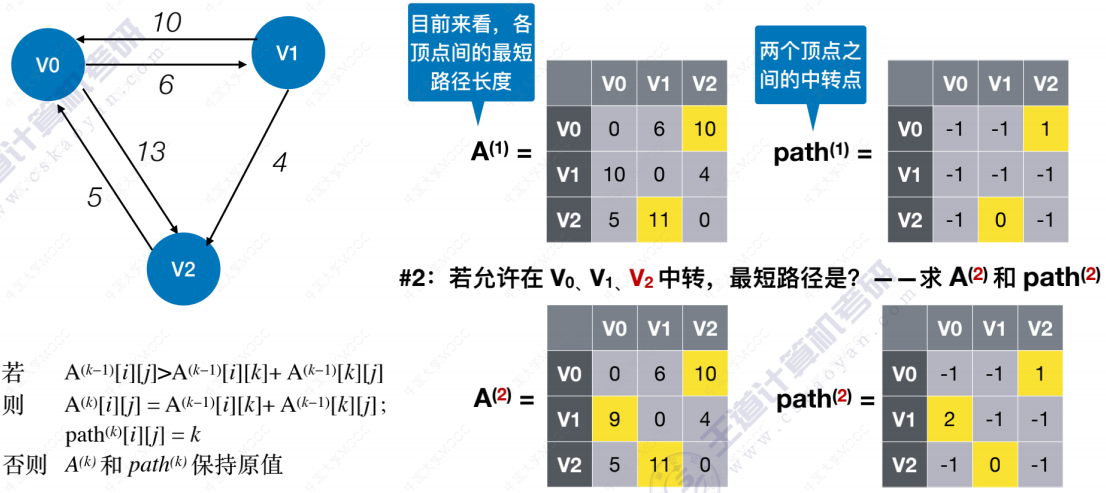
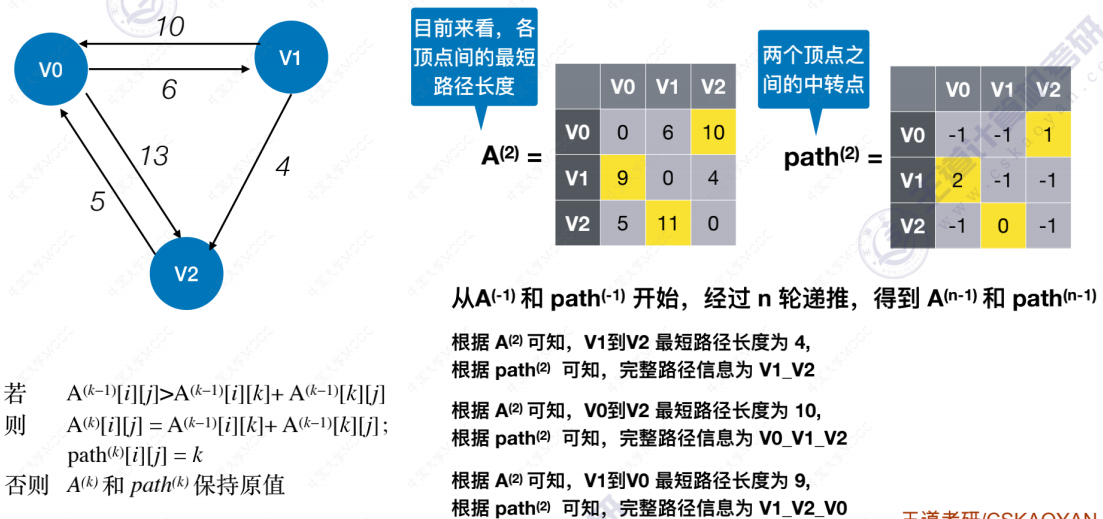
 拓扑排序
拓扑排序
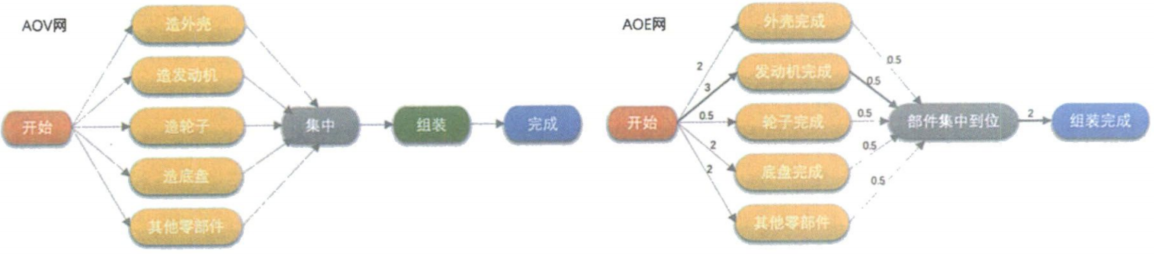
在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网,我们称为AOV网。
 所谓拓扑排序,其实就是对一个有向图构造拓扑排序的过程。
所谓拓扑排序,其实就是对一个有向图构造拓扑排序的过程。
拓扑排序算法
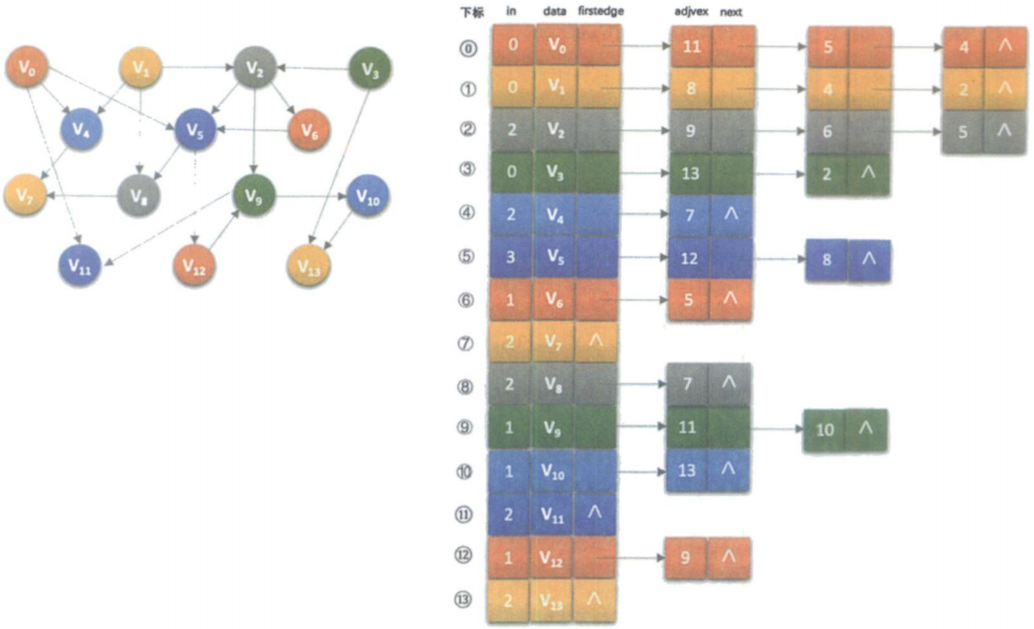
 由于拓扑排序的过程中需要删除顶点,用邻接表会更加方便。考虑到算法过程中始终要查找入度为0的顶点,我们在原来顶点表结点结构中,增加一个入度域in,其中in就是入度的数字。
由于拓扑排序的过程中需要删除顶点,用邻接表会更加方便。考虑到算法过程中始终要查找入度为0的顶点,我们在原来顶点表结点结构中,增加一个入度域in,其中in就是入度的数字。
![]()
/* 邻接表结构****************** */
typedef struct EdgeNode /* 边表结点 */
{int adjvex; /* 邻接点域,存储该顶点对应的下标 */int weight; /* 用于存储权值,对于非网图可以不需要 */struct EdgeNode *next; /* 链域,指向下一个邻接点 */
}EdgeNode;typedef struct VertexNode /* 顶点表结点 */
{int in; /* 顶点入度 */int data; /* 顶点域,存储顶点信息 */EdgeNode *firstedge;/* 边表头指针 */
}VertexNode, AdjList[MAXVEX];typedef struct
{AdjList adjList; int numVertexes,numEdges; /* 图中当前顶点数和边数 */
}graphAdjList,*GraphAdjList;借助栈这种数据结构, 最开始先让入度为0的结点入栈,然后弹出一个入度为0的结点并修改其他结点的入度,如果有为0的入栈,依次循环。
/* 拓扑排序,若GL无回路,则输出拓扑排序序列并返回1,若有回路返回0。 */
Status TopologicalSort(GraphAdjList GL)
{ EdgeNode *e; int i,k,gettop; int top=0; /* 用于栈指针下标 */int count=0;/* 用于统计输出顶点的个数 */ int *stack; /* 建栈将入度为0的顶点入栈 */ stack=(int *)malloc(GL->numVertexes * sizeof(int) ); for(i = 0; inumVertexes; i++) if(0 == GL->adjList[i].in) /* 将入度为0的顶点入栈 */ stack[++top]=i; while(top!=0) { gettop=stack[top--]; printf("%d -> ",GL->adjList[gettop].data); count++; /* 输出i号顶点,并计数 */ for(e = GL->adjList[gettop].firstedge; e; e = e->next) { k=e->adjvex; if( !(--GL->adjList[k].in) ) /* 将i号顶点的邻接点的入度减1,如果减1后为0,则入栈 */ stack[++top]=k; }} printf("\n"); if(count < GL->numVertexes) return ERROR; else return OK;
} 关键路径
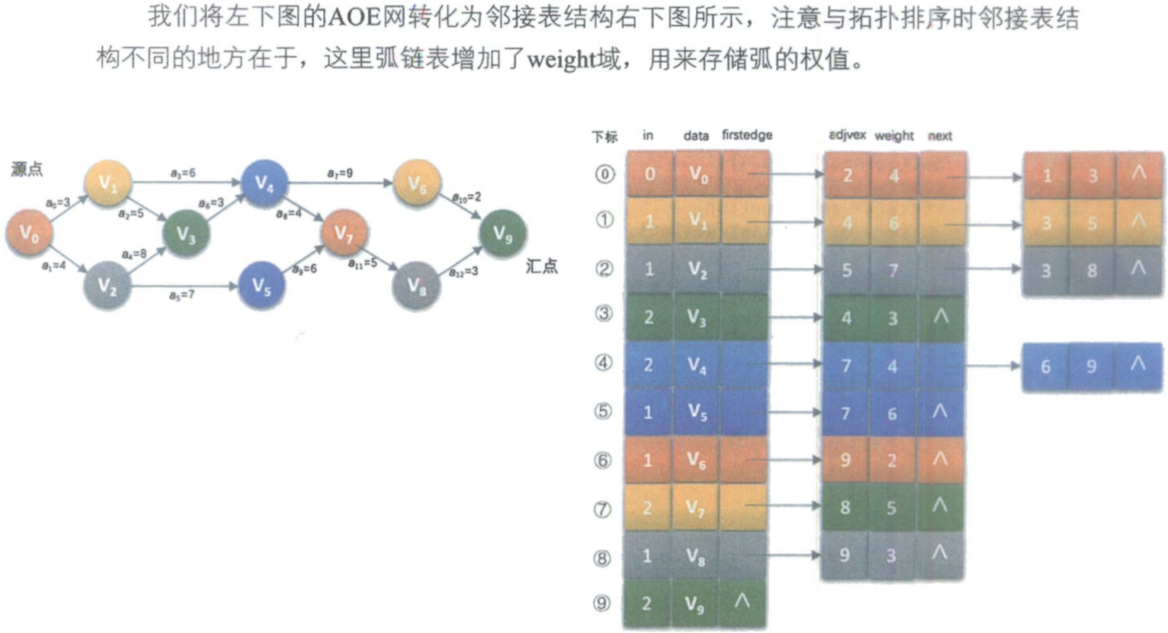
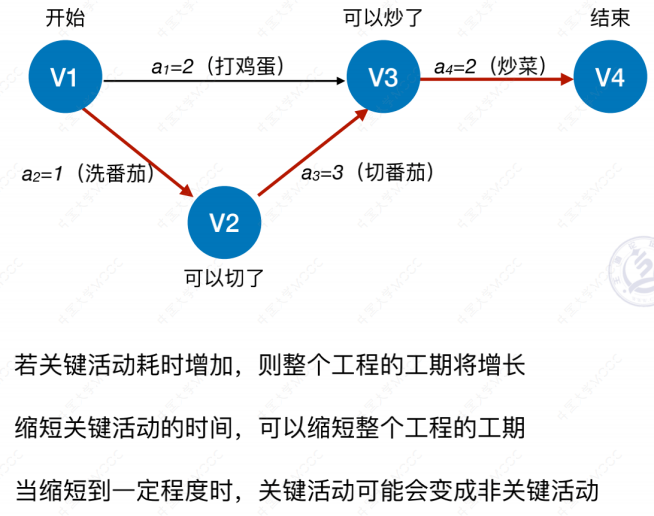
在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动 ,用边上的权值表示活动的持续时间,这种有向图的边表示活动的网,我们称之为AOE网。我们把AOE网中没有入边的顶点称为始点或源点,没有出边的顶点称为终点或汇点。由于一个工程,总有一个开始,一个结束,所以正常情况下,AOE网只有一个源点一个汇点。

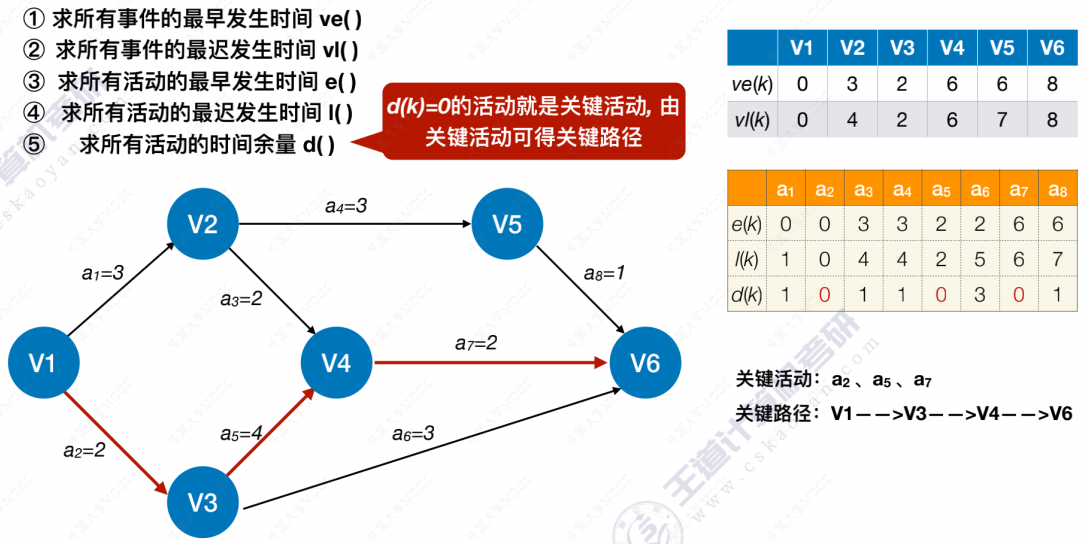
关键路径算法的原理
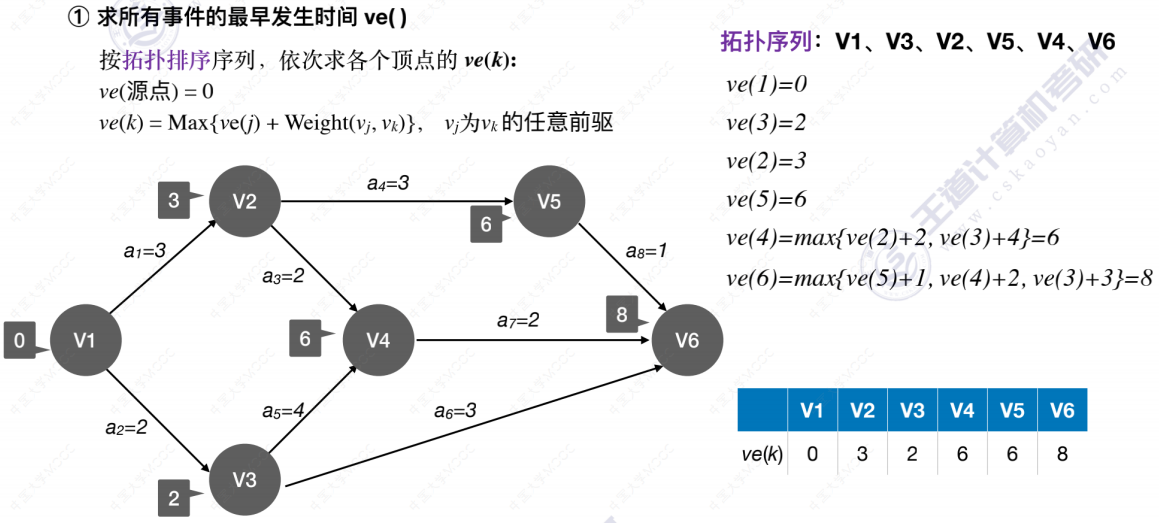
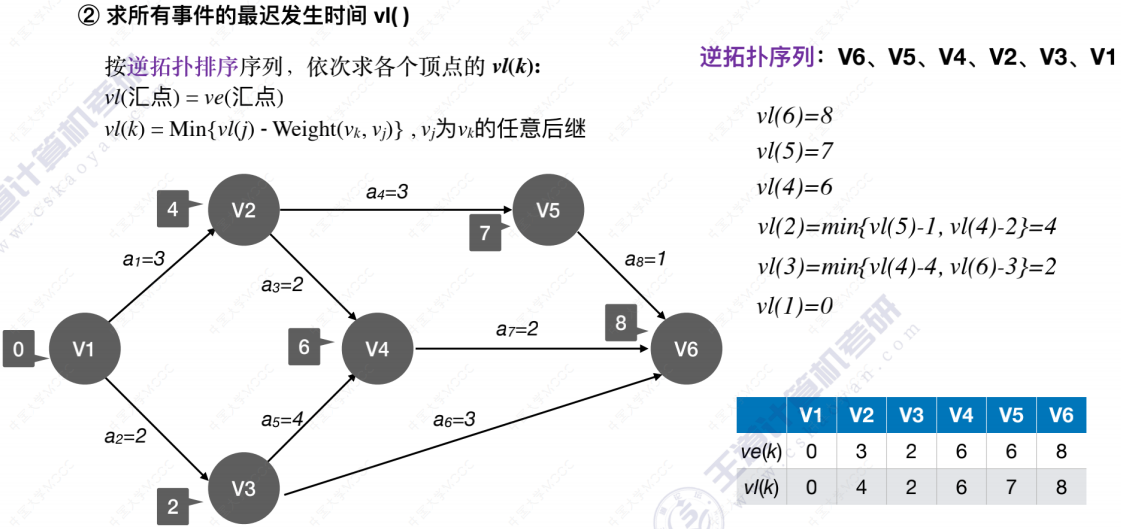
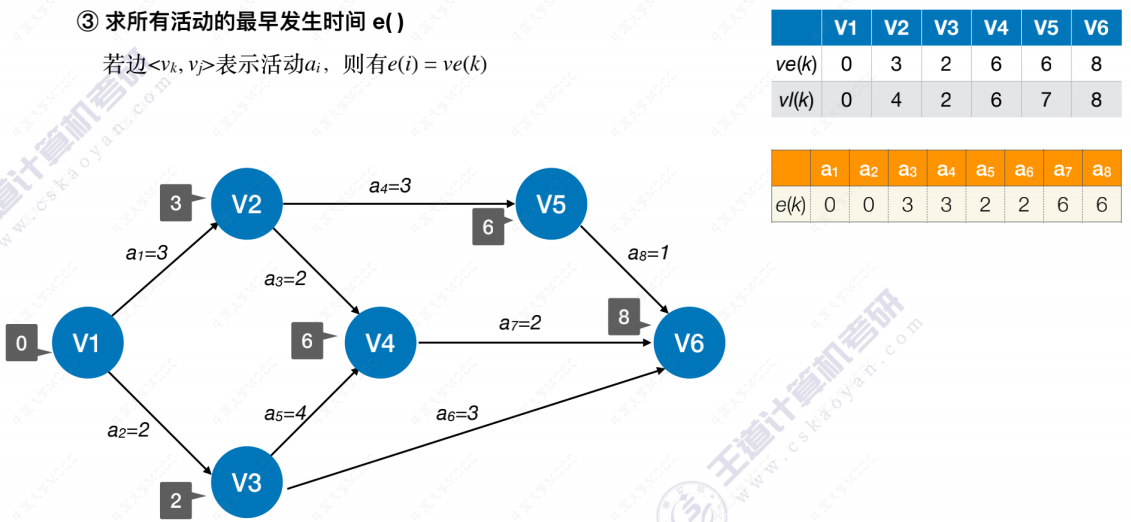
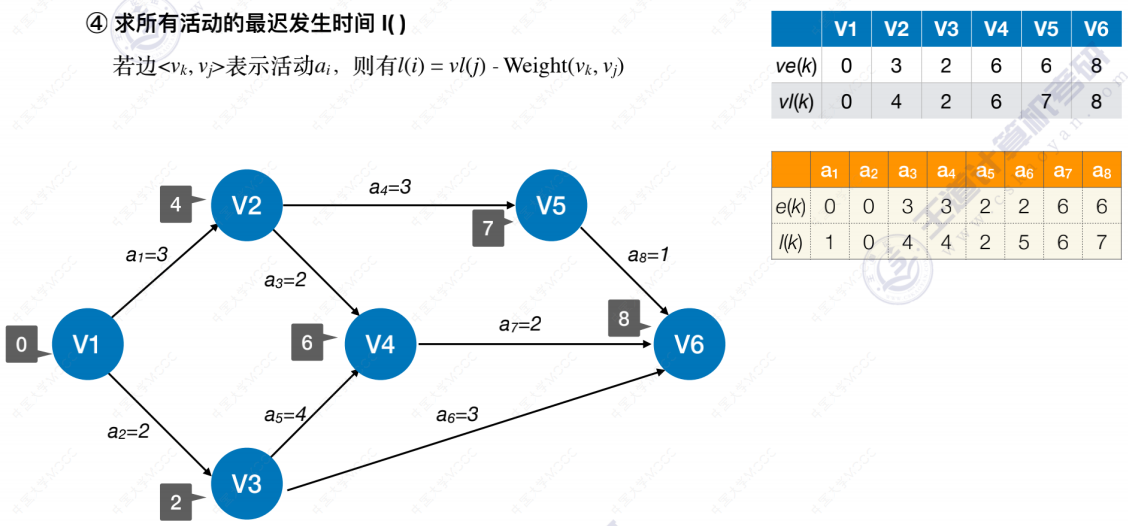
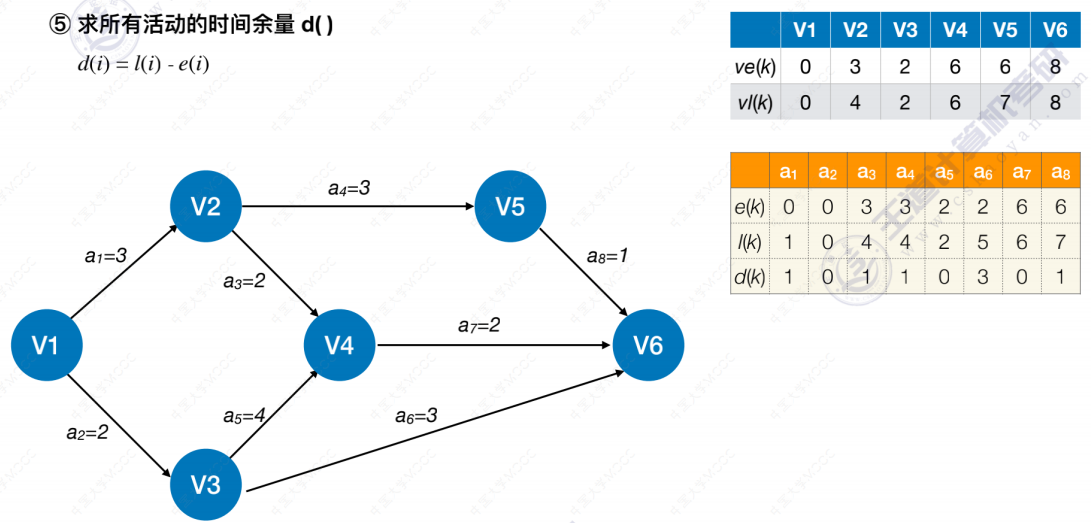
我们需要找到所有活动的最早开始时间和最晚开始时间,并且比较它们,如果相等就意味着此活动是关键活动,活动间的路径为关键路径。如果不等,则就不是。
 关键路径算法
关键路径算法

int *etv,*ltv; /* 事件最早发生时间和最迟发生时间数组 */
int *stack2; /* 用于存储拓扑序列的栈 */
int top2; /* 用于stack2的指针 *//* 拓扑排序 */
Status TopologicalSort(GraphAdjList GL)
{ /* 若GL无回路,则输出拓扑排序序列并返回1,若有回路返回0。 */ EdgeNode *e; int i,k,gettop; int top=0; /* 用于栈指针下标 */int count=0;/* 用于统计输出顶点的个数 */ int *stack; /* 建栈将入度为0的顶点入栈 */ stack=(int *)malloc(GL->numVertexes * sizeof(int) ); for(i = 0; inumVertexes; i++) if(0 == GL->adjList[i].in) /* 将入度为0的顶点入栈 */ stack[++top]=i; top2=0; etv=(int *)malloc(GL->numVertexes * sizeof(int) ); /* 事件最早发生时间数组 */ for(i=0; inumVertexes; i++) etv[i]=0; /* 初始化 */stack2=(int *)malloc(GL->numVertexes * sizeof(int) );/* 初始化拓扑序列栈 */printf("TopologicalSort:\t");while(top!=0) { gettop=stack[top--]; printf("%d -> ",GL->adjList[gettop].data); count++; /* 输出i号顶点,并计数 */ stack2[++top2]=gettop; /* 将弹出的顶点序号压入拓扑序列的栈 */for(e = GL->adjList[gettop].firstedge; e; e = e->next) { k=e->adjvex; if( !(--GL->adjList[k].in) ) /* 将i号顶点的邻接点的入度减1,如果减1后为0,则入栈 */ stack[++top]=k; if((etv[gettop] + e->weight)>etv[k]) /* 求各顶点事件的最早发生时间etv值 */ etv[k] = etv[gettop] + e->weight;} } printf("\n"); if(count < GL->numVertexes) return ERROR; else return OK;
}/* 求关键路径,GL为有向网,输出G的各项关键活动 */
void CriticalPath(GraphAdjList GL)
{ EdgeNode *e; int i,gettop,k,j; int ete,lte; /* 声明活动最早发生时间和最迟发生时间变量 */ TopologicalSort(GL); /* 求拓扑序列,计算数组etv和stack2的值 */ ltv=(int *)malloc(GL->numVertexes*sizeof(int));/* 事件最早发生时间数组 */ for(i=0; inumVertexes; i++) ltv[i]=etv[GL->numVertexes-1]; /* 初始化 */ printf("etv:\t"); for(i=0; inumVertexes; i++) printf("%d -> ",etv[i]); printf("\n"); while(top2!=0) /* 出栈是求ltv */ { gettop=stack2[top2--]; for(e = GL->adjList[gettop].firstedge; e; e = e->next) /* 求各顶点事件的最迟发生时间ltv值 */ { k=e->adjvex; if(ltv[k] - e->weight < ltv[gettop]) ltv[gettop] = ltv[k] - e->weight; } } printf("ltv:\t"); for(i=0; inumVertexes; i++) printf("%d -> ",ltv[i]); printf("\n"); for(j=0; jnumVertexes; j++) /* 求ete,lte和关键活动 */ { for(e = GL->adjList[j].firstedge; e; e = e->next) { k=e->adjvex; ete = etv[j]; /* 活动最早发生时间 */ lte = ltv[k] - e->weight; /* 活动最迟发生时间 */ if(ete == lte) /* 两者相等即在关键路径上 */ printf(" length: %d \n",GL->adjList[j].data,GL->adjList[k].data,e->weight);} }
}