【刷题之路Ⅱ】将你的二分法修炼到极致！LeetCode 34. 在排序数组中查找元素的第一个和最后一个位置

• 一、题目描述
• 二、解题
• • 1、方法1——暴力法1——直接遍历
  • • 1.1、思路分析
    • 1.2、代码实现
  • 2、方法2——暴力法2——前后扫描
  • • 2.1、思路分析
    • 2.2、代码实现
  • 3、方法3——直接二分法
  • • 3.1、思路分析
    • 3.2、代码实现
    • 3.3、补充
  • 4、方法4——二分后扩散
  • • 4.1、思路分析
    • 4.2、代码实现
  • 5、递归二分判断边界
  • • 5.1、思路分析
    • 5.2、代码实现

一、题目描述

原题连接： 34. 在排序数组中查找元素的第一个和最后一个位置
题目描述：
给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target，返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：
输入： nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：
输入： nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：
输入： nums = [], target = 0
输出：[-1,-1]

二、解题

1、方法1——暴力法1——直接遍历

1.1、思路分析

第一个当然是我们万能的暴力法：
利用数组的有序性从头到尾遍历一遍数组，
第一次，检查遍历到的元素是否等于target，遇到刚好等于target的时候，记录当前的位置；
然后接着往后遍历，检查遍历到的元素是否不等于target遇到刚好不等于target的时候，记录当前位置的前一个位置即可。

1.2、代码实现

// 有了以上思路，那我们写起代码来也就水到渠成了：

int* searchRange1(int* nums, int numsSize, int target, int* returnSize) {assert(nums && returnSize);*returnSize = 2;int* ans = (int*)malloc(2 * sizeof(int)); // 模拟出一个要返回的数组if (NULL == ans) {perror("searchRange1");return NULL;}ans[0] = -1;ans[1] = -1;int i = 0;int j = 0;if (0 == numsSize) {return ans;}for (i = 0; i < numsSize; i++) {if (nums[i] == target) {ans[0] = i;for (j = i; j < numsSize; j++) {if (j == numsSize - 1 && nums[j] == target) {ans[1] = j;}else if (nums[j] == target && nums[j + 1] != target) {ans[1] = j;break;}}}if (ans[0] != -1) {break;}}return ans;
}

时间复杂度：O(n)，n为数组元素个数。
空间复杂度：O(1)，我们只需要用到常数级的额外空间。

2、方法2——暴力法2——前后扫描

2.1、思路分析

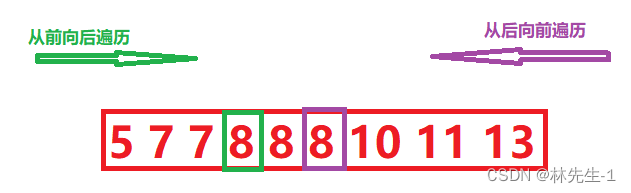
暴力法1太过白目，其实我们可以先从前往后遍历当第一次遇到nums[i] == target时，说明nums[i]是数组中第一次出现的target，记录其下标并跳出循环。
然后在从后往前遍历(这次我们只需要从后向前遍历到target第一次出现的下标即可)，当第一次遇到nums[i] == target时，说明nums[i]是数组中最后一次出现的target，记录其下标并跳出循环，就结束了。

2.2、代码实现

有了以上思路，那我们写起代码来也就水到渠成了：

int* searchRange2(int* nums, int numsSize, int target, int* returnSize) {assert(nums && returnSize);*returnSize = 2;int* ans = (int*)malloc(2 * sizeof(int));if (NULL == ans) {perror("searchRange2");return NULL;}ans[0] = -1;ans[1] = -1;int i = 0;// 找到ans[0]for (i = 0; i < numsSize; i++) {if (nums[i] == target) {ans[0] = i;break;}}// 找到ans[1]for (i = numsSize - 1; i >= 0; i--) {if (nums[i] == target) {ans[1] = i;break;}}return ans;
}

时间复杂度：O(n)，其中n为数组元素个数，最坏情况下我们需要遍历一遍数组。
空间复杂度：O(1)，我们只需要用到常数级的额外空间。

3、方法3——直接二分法

3.1、思路分析

题目要求我们使用时间复杂度为O(logn)的算法，已经在暗示我们要使用二分查找法了，我们可以先分别找出出现第一次的target的下标和出现最后一次的target的下标，然后将它们写进数组，返回即可。
我们可以分别定义两个函数get_first和get_last来帮我们找到出现第一和最后一次出现的target的下标。
在这两个函数里，关于nums[mid] < target 和nums[mid] > target 这两种情况的分析和普通的二分法没有区别。
只是在nums[mid] == target时就要特别分析了：
在get_first中，当出现nums[mid] == target时，因为我们要找的是第一次出现的target，所以我们还是要继续向左找，所以
这里的操作是right = mid：

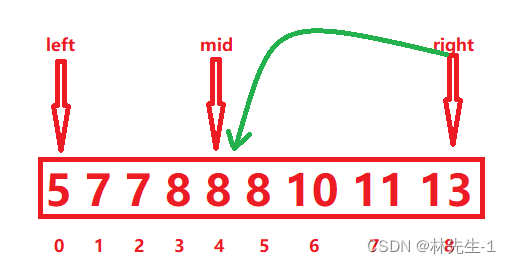
(这里的target假设是8)
在get_last中，当出现nums[mid] == target时，因为我们要找的是最后一次出现的target，所以我们还是要继续向右找，所以
这里的操作是left = mid：

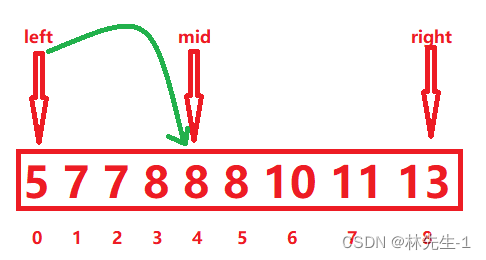
而且，当我们找target第一次出现的下标之后，就可以确定target最后一次出现的下标的范围一定是在第一次出现的下标之后的后半部分，所以我们在找target最后一次出现的下标的时候就可以缩小范围了。
get_first和get_last如果找不到target的话，就返回-1；

3.2、代码实现

有了以上思路，那我们写起代码来也就水到渠成了：

// 写一个二分查找法，返回target第一次出现的下标。
int get_first(int* nums, int left, int right, int target) {assert(nums);int mid = 0;while (left < right) {mid = left + (right - left) / 2;if (target < nums[mid]) {right = mid - 1;}else if (target > nums[mid]) {left = mid + 1;}else {right = mid;}}return nums[left] == target ? left : -1;
}// 写一个二分查找法，返回target最后一次出现的下标
int get_last(int* nums, int left, int right, int target) {assert(nums);int mid = 0;while (left < right) {mid = left + (right - left + 1) / 2;if (target < nums[mid]) {right = mid - 1;}else if (target > nums[mid]) {left = mid + 1;}else {left = mid;}}return left;
}
int* searchRange3(int* nums, int numsSize, int target, int* returnSize) {assert(nums && returnSize);*returnSize = 2;int* ans = (int*)malloc(2 * sizeof(int));if (NULL == ans) {perror("searchRange3");return NULL;}ans[0] = -1;ans[1] = -1;if (0 == numsSize) {return ans;}ans[0] = get_first(nums, 0, numsSize - 1, target);if (-1 == ans[0]) {return ans;}ans[1] = get_last(nums, ans[0], numsSize - 1, target);return ans;
}

// 时间复杂度：O(logn)，n为数组元素个数。
// 空间复杂度：O(1)，我们只需要用到常数级的额外空间。

3.3、补充

可能有的朋友不懂为什么在get_last函数中mid的计算方法变成了mid = left + (right - left + 1) / 2(也就是mid = (left + right + 1) / 2)。
其实这也是为了防止一些特殊情况的发生，比如说下面这个例子：

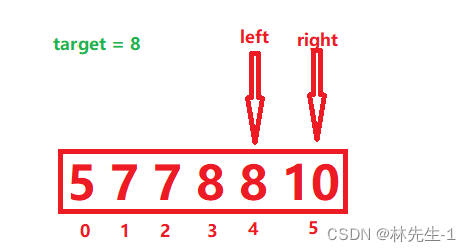
这个例子执行到最后肯定会出现这样的情况，如果这时还是使用的mid = (left + right) / 2，那mid的值就等于4，然后发现nums[mid] == target,
然后又执行left = mid，但执行后left还是等于4，这就等于根本没动啊。
这就使得程序最后死循环了。
所以我们这里应该改成mid = (left + right + 1) / 2。以保证范围能够向右边逼近。
向下取整对于我们向左边逼近是有利的，而向上取整则对我们向右边逼近有利。

4、方法4——二分后扩散

4.1、思路分析

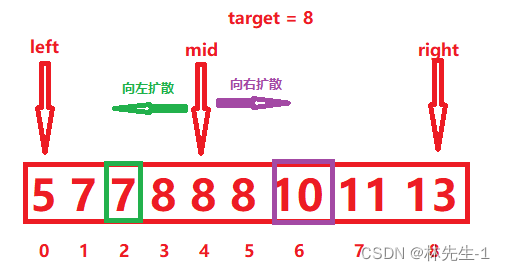
既然题目已经说了是非降序的数组，那么相同的元素一定是紧挨在一起的，所以我们可以利用二分法找到一个target之后，在以nums[mid]为中心向两边扩散，观察两边有多少个元素与target相同。
找到一个不同就停止扩散，记录其前一个或后一个下标：

4.2、代码实现

有了以上思路，那我们写起代码来也就水到渠成了：

int* searchRange4(int* nums, int numsSize, int target, int* returnSize) {assert(nums && returnSize);*returnSize = 2;int* ans = (int*)malloc(2 * sizeof(int));if (NULL == ans) {perror("searchRange4");return NULL;}ans[0] = -1;ans[1] = -1;int left = 0;int right = numsSize - 1;int mid = 0;while (left <= right) {mid = left + (right - left) / 2;if (target < nums[mid]) {right = mid - 1;}else if (target > nums[mid]) {left = mid + 1;}else {break;}}if (left > right) { // 说明找不到return ans;}left = mid;right = mid;// 向左边扩散while (nums[left] == target && --left >= 0) {;}ans[0] = left + 1;// 向右边扩散while (nums[right] == target && ++right < numsSize) {;}ans[1] = right - 1;return ans;
}

时间复杂度：O(n)，n为数组元素个数，最坏的情况下，我们还是要遍历一遍数组。
空间复杂度：O(1)，我们只需要用到常数级的额外空间。

5、递归二分判断边界

5.1、思路分析

有没有感觉这一题和我们之前做过的一题："牛客 NC105 二分查找-II"有点儿相像？
确实，NC105要求的是第一次出现的下标，而我们这一题要求的是第一次最后一次的下标。
可以说我们这一题已经包含了NC105了。
在解析NC105时，我写过一个递归版本的二分判断左边界的，那我们是否可以反向思考，是否也写出一个递归版本的二分判断右边界呢？
其实是完全可以的，我们需要做的只是更改一下递归结束的判断条件(改成nums[right] == target)和nums[mid]和target相等时逼近的方向(改成向右边逼近)即可。

5.2、代码实现

有了以上思路，那我们写起代码来也就水到渠成了：

// 先写一个递归版的二分查找——返回左边界
int binary_search_left(int* nums, int left, int right, int target) {assert(nums);if (left > right) {return -1;}if (nums[left] == target) {return left;}int mid = left + (right - left) / 2;if (target < nums[mid]) {return binary_search_left(nums, left, mid - 1, target);}else if (target > nums[mid]) {return binary_search_left(nums, mid + 1, right, target);}else {return binary_search_left(nums, left, mid, target); // 如果相等，就往左边逼近}
}// 再写一个递归版的二分查找——返回右边界
int binary_search_right(int* nums, int left, int right, int target) {assert(nums);if (left > right) {return -1;}if (nums[right] == target) {return right;}int mid = left + (right - left + 1) / 2;if (target < nums[mid]) {return binary_search_right(nums, left, mid - 1, target);}else if (target > nums[mid]) {return binary_search_right(nums, mid + 1, right, target);}else {return binary_search_right(nums, mid, right, target); // 如果相等，就往右边逼近}
}int* searchRange5(int* nums, int numsSize, int target, int* returnSize) {assert(nums && returnSize);*returnSize = 2;int* ans = (int*)malloc(2 * sizeof(int));if (NULL == ans) {perror("searchRange5");return NULL;}ans[0] = -1;ans[1] = -1;ans[0] = binary_search_left(nums, 0, numsSize - 1, target);if (-1 == ans[0]) {return ans;}ans[1] = binary_search_right(nums, ans[0], numsSize - 1, target);return ans;
}