机器学习(课堂笔记)Day08:逻辑回归 Logistic Regression
0x00 什么是逻辑回归 Logistic Regression
逻辑回归:逻辑回归既是一个回归算法,也是一个分类算法,通常用来解决二分类问题
回归算法如何解决分类问题呢?
逻辑回归的预测值是一个概率值,我们根据概率值的大小进行分类。概率值可以被解释为输入样本属于某个类别的概率。逻辑回归中使用 Sigmoid 函数(逻辑函数)将线性回归的预测值映射为0和1之间的概率值。
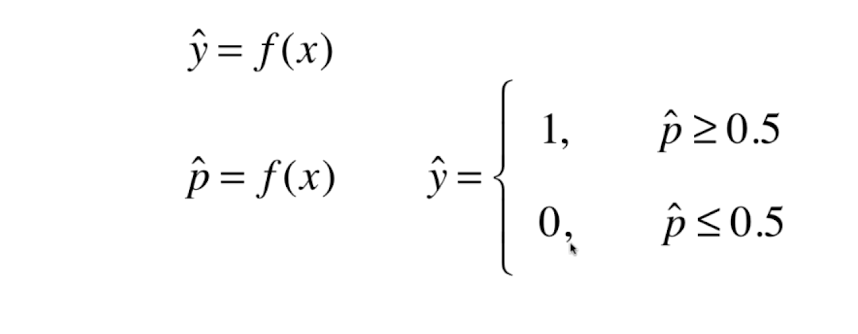
例如:给你一个病人的信息,你计算出该病人得恶性肿瘤的概率,当该概率大于0.5时,我们将其分类为恶性肿瘤,当该概率小于0.5时,我们将其分类为良性肿瘤。
逻辑回归如何进行预测概率值呢?
我们之间讨论的线性回归,直接通过训练数据集 得到模型参数theta ,然后theta 和 新样本矩阵 点乘就可以得到预测值向量。但是因为概率值的值域范围必定是在[0,1]之间的,所以我们还需要将预测值向量送入一个称为sigmoid的函数中,将其映射到[0,1]之间。


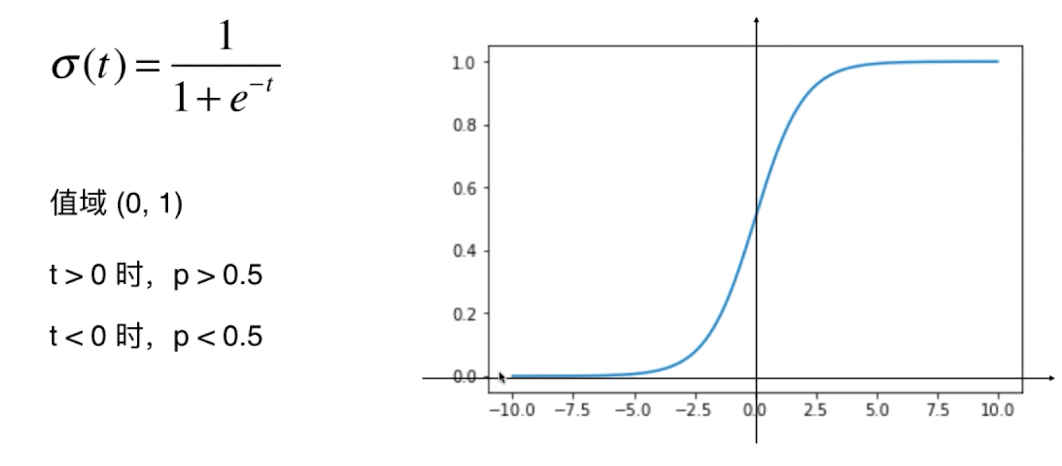
分析:
当t趋近与正无穷时,函数值无限逼近1
当t趋近与负无穷时,函数值无限逼近0
当t等于0时,函数值为1/2
编程实现:
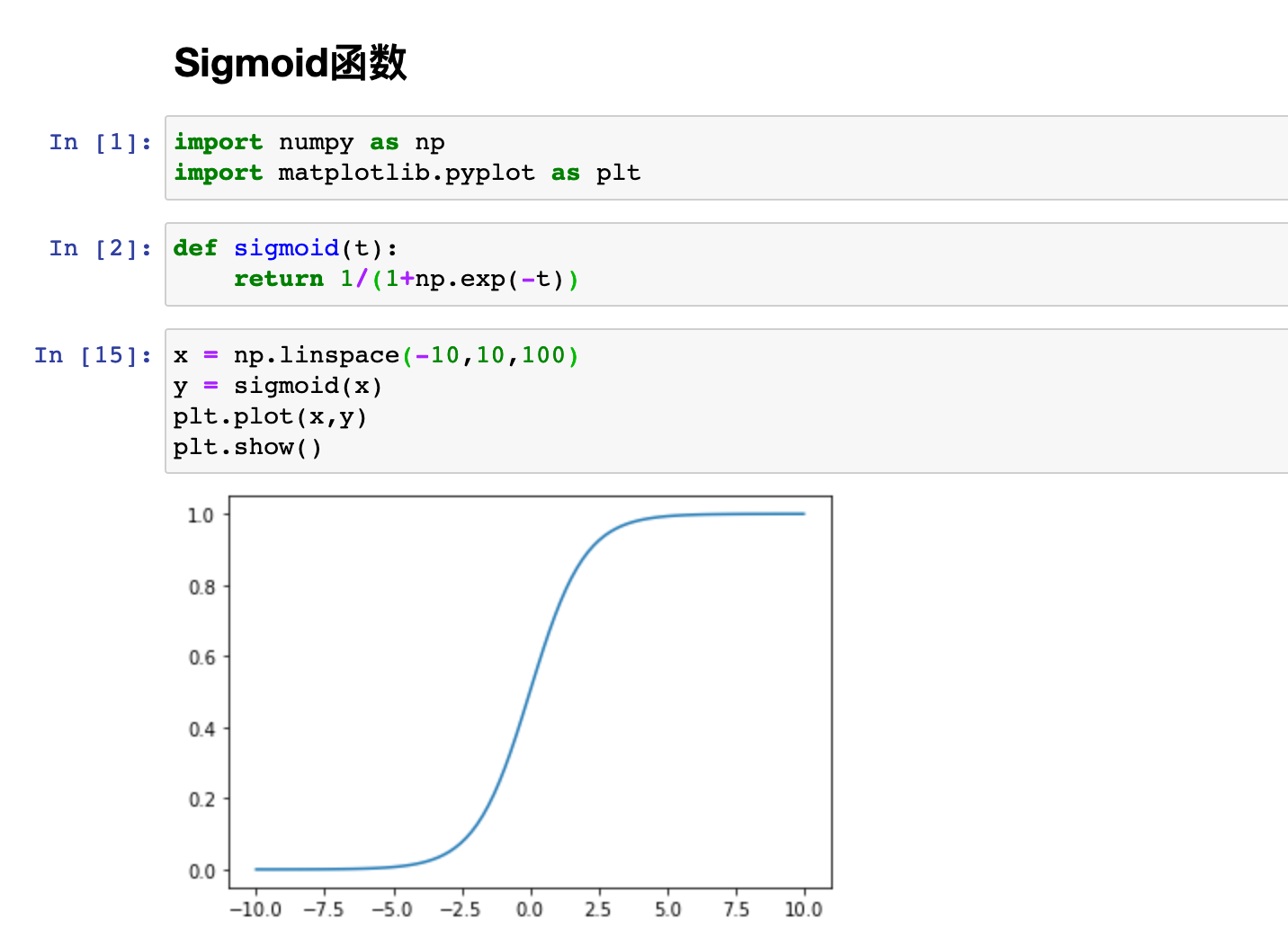

0x01 逻辑回归的损失函数
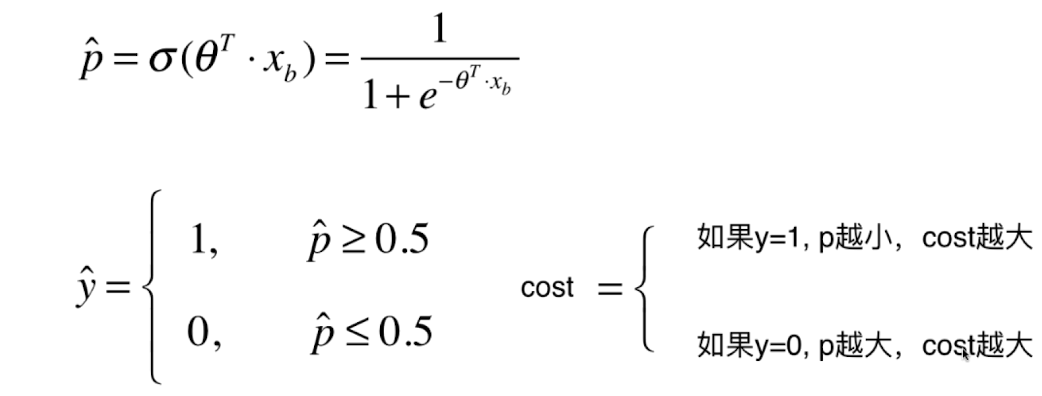

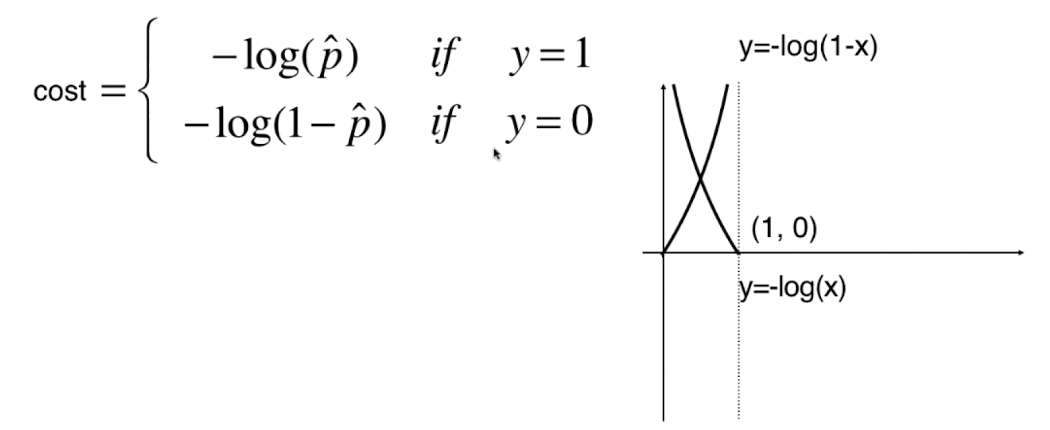
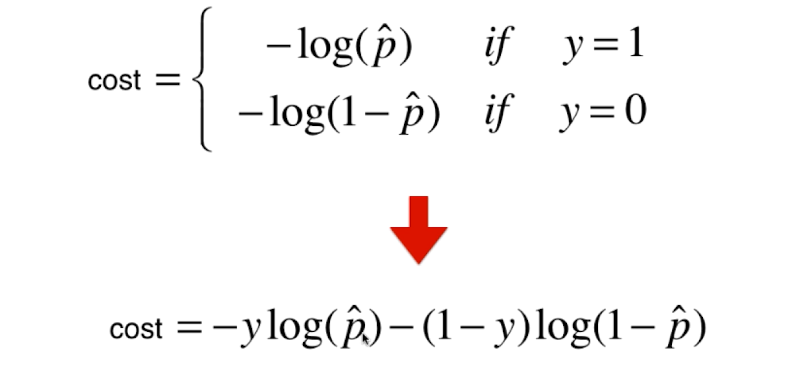

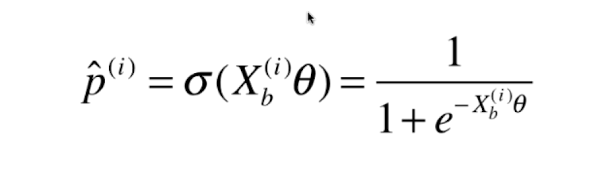
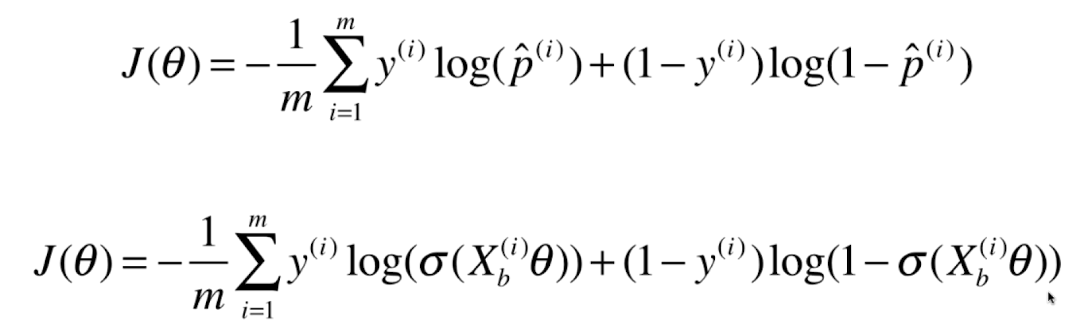
该损失函数没有公式解,只能使用梯度下降法求解。
0x02 逻辑回归损失函数的梯度

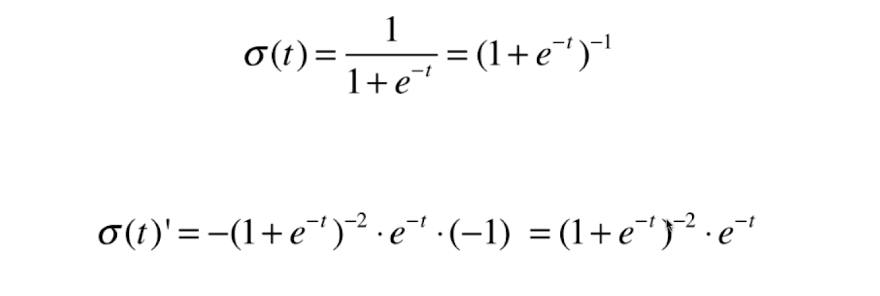
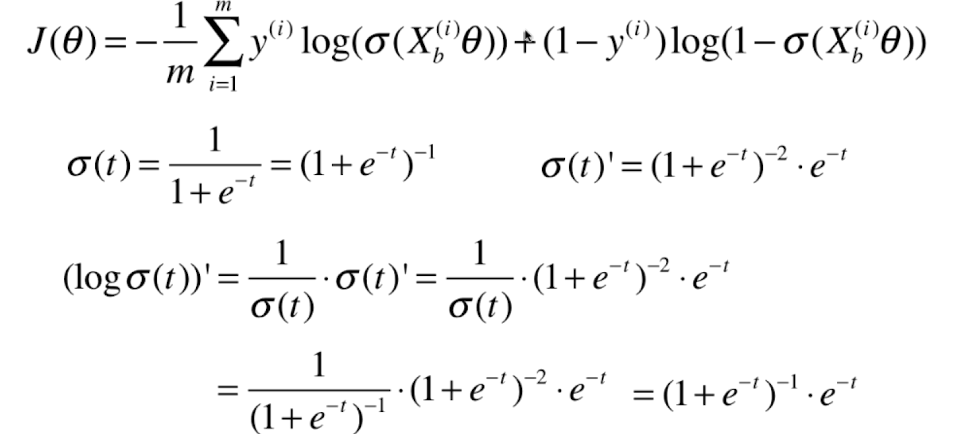
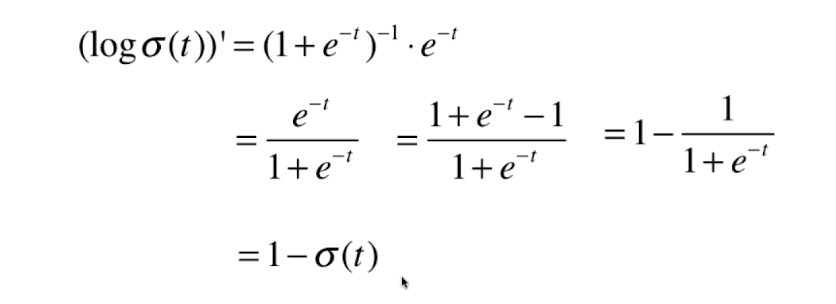
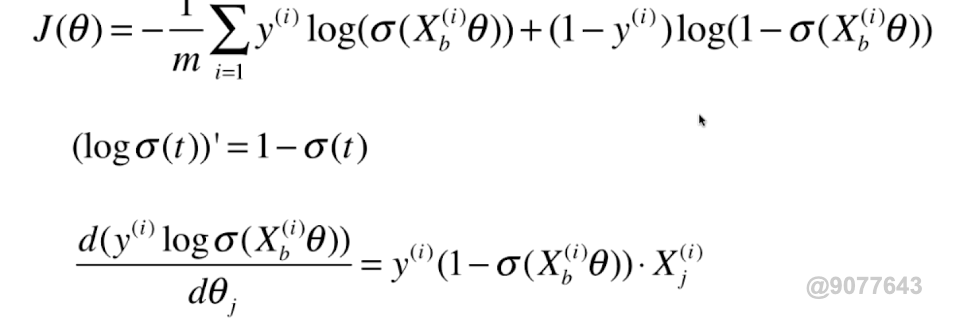
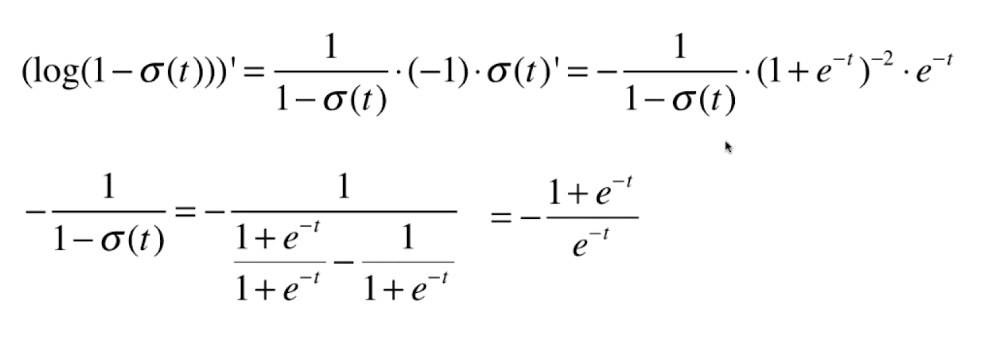
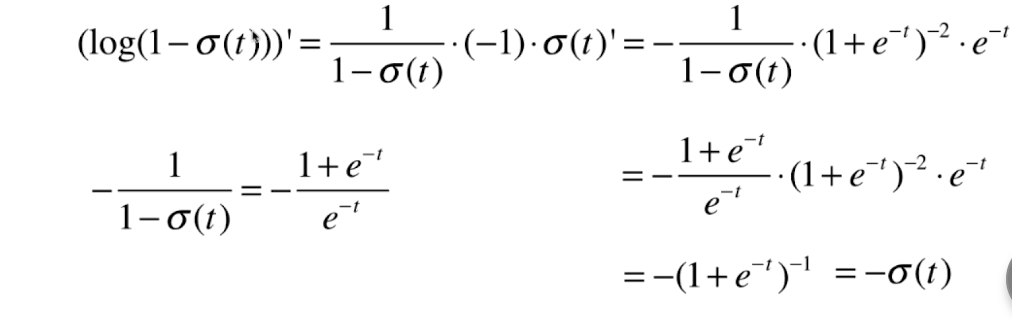
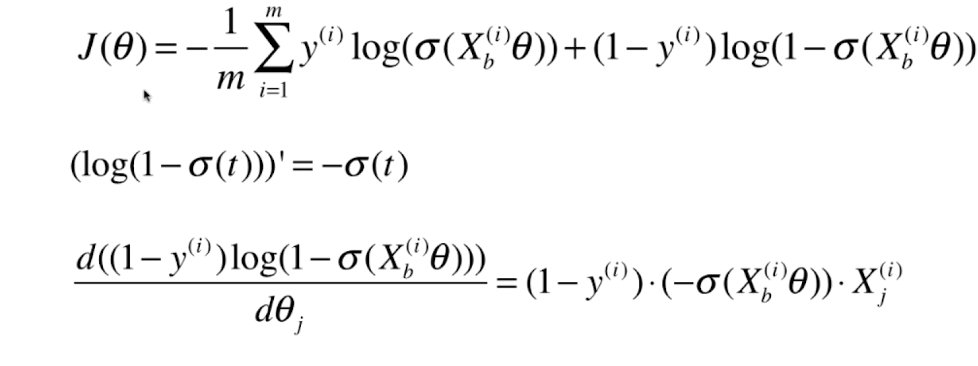
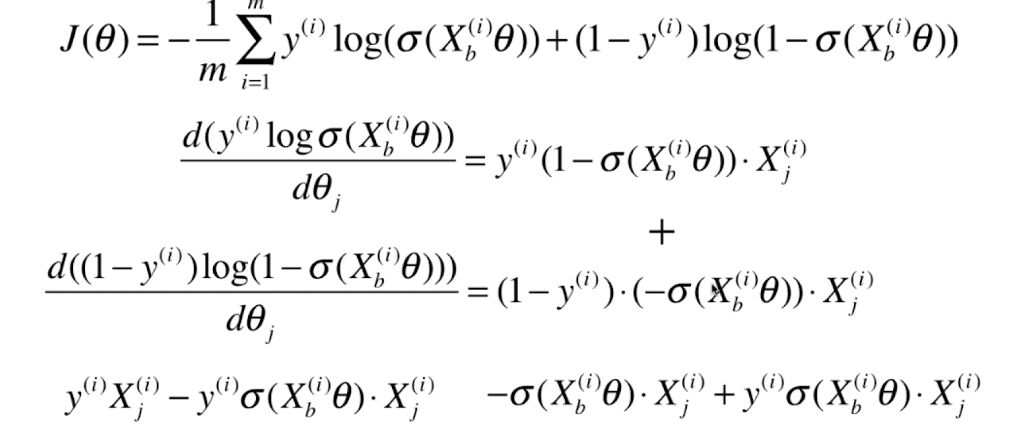
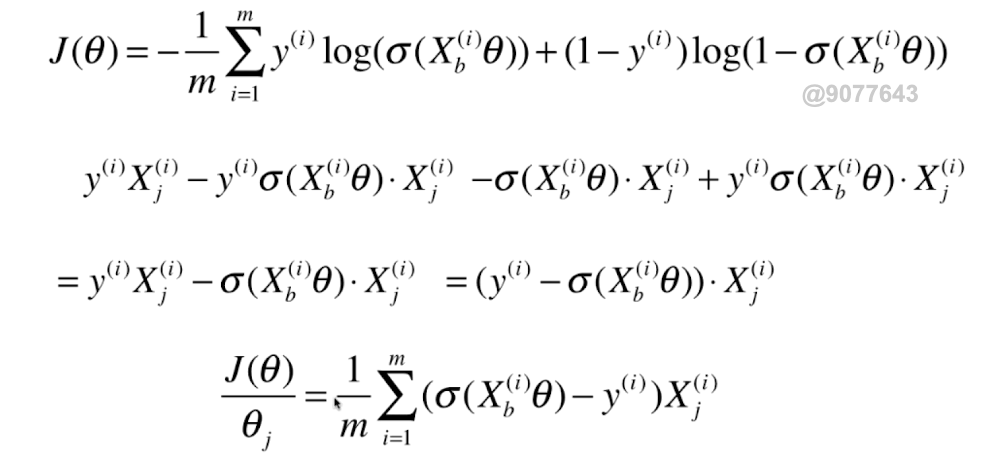
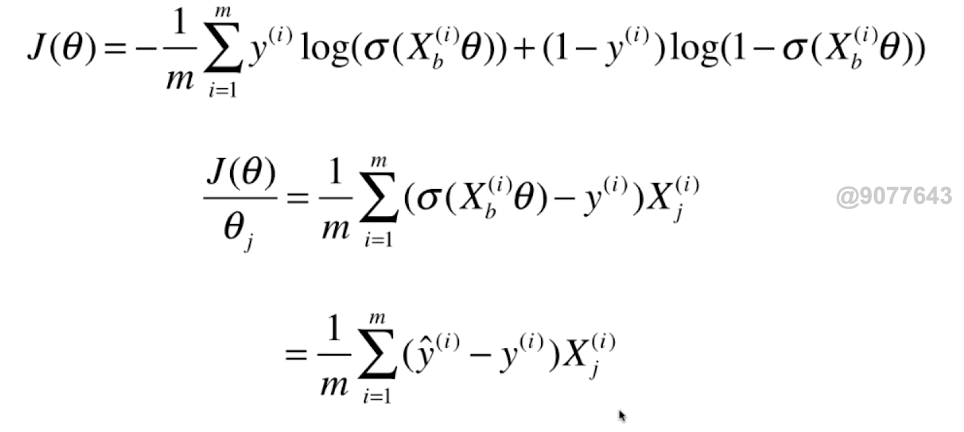

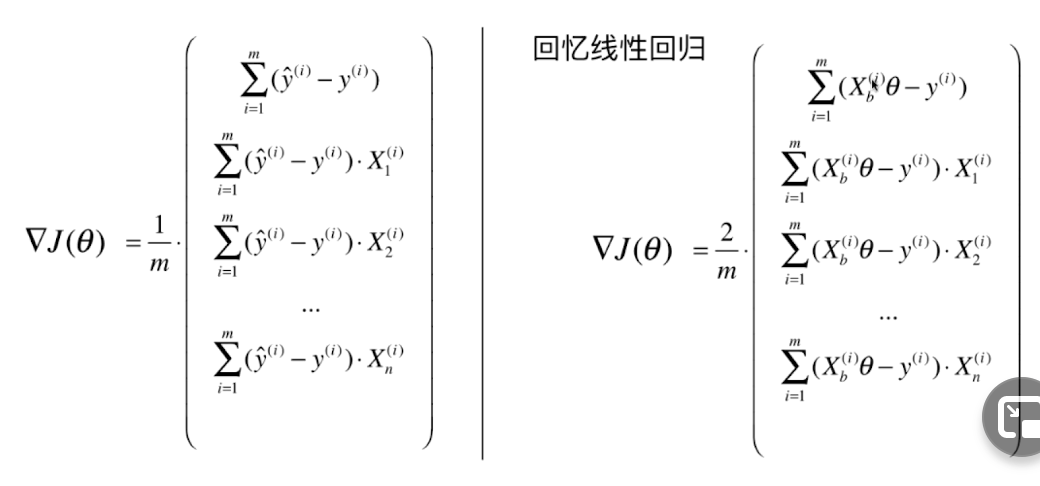
向量化:
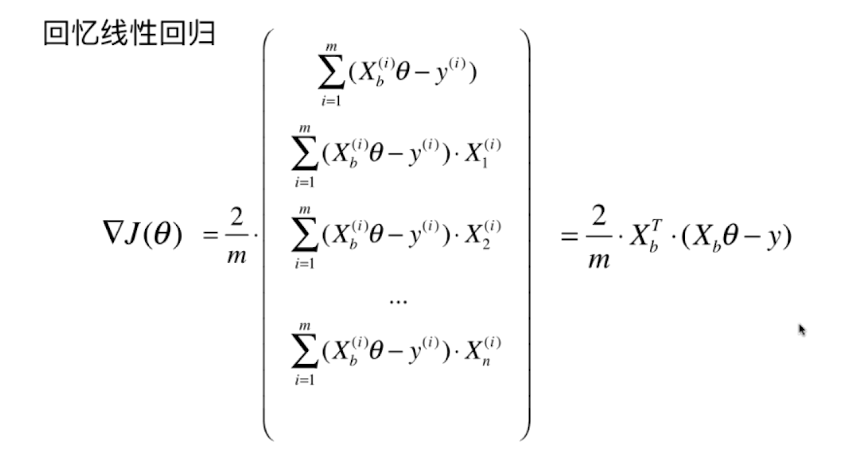
对逻辑回归的梯度进行向量化:
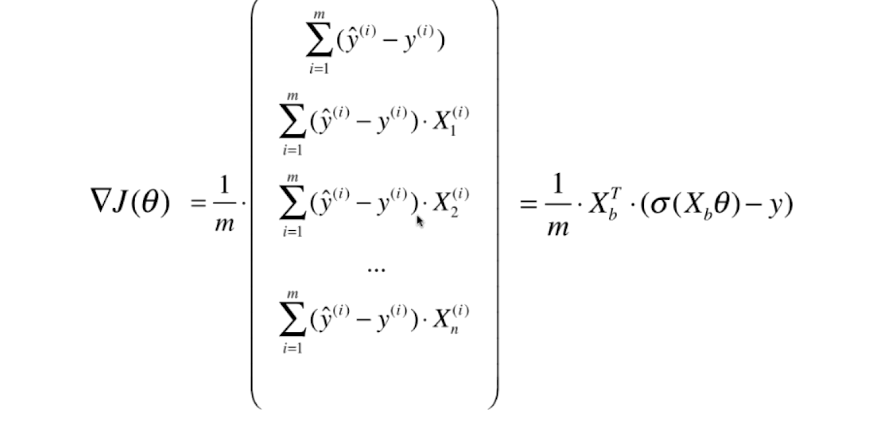
0x03 实现逻辑回归算法
'''
Author: your name
Date: 2020-11-12 14:21:32
LastEditTime: 2020-12-03 14:58:50
LastEditors: Please set LastEditors
Description: In User Settings Edit
FilePath: /ML/playML/LinearRegression.py
'''
import numpy as np
from .metrics import accuracy_scoreclass LogisticRegression:def __init__(self):self.coef_ = None # 系数self.interception = None # 截距self._theta = None # θdef _sigmoid(self,t):return 1./(1.+np.exp(-t))# 批量梯度下降法def fit(self, X_train, y_train, eta=0.01, n_iters=1e4):#损失函数def J(theta, X_b, y):y_hat = self._sigmoid(X_b.dot(theta))try:return -np.sum(y*np.log(y_hat)+(1-y)*np.log(1-y_hat))/len(y)# theta 向量 和 X 列向量 相乘 就是预测结果组成的向量except:return float('inf')def dJ(theta, X_b, y): """ 向量化的方式計算梯度 """return X_b.T.dot(self._sigmoid( X_b.dot(theta) )-y ) / len(X_b)def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):theta = initial_thetai_iter = 0while i_iter < n_iters:gradient = dJ(theta, X_b, y)last_theta = thetatheta = theta - eta*gradientif(abs(J(theta, X_b, y)-J(last_theta, X_b, y)) < epsilon):breaki_iter += 1return thetaX_b = np.hstack([np.ones((len(X_train), 1)), X_train])initial_theta = np.zeros(X_b.shape[1]) # 等于Xb的列数self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)self.interception = self._theta[0]self.coef_ = self._theta[1:]return self def predict_proba(self, X_predict):""" 給定待預測的數據集 X_predict ,返回y_predict對應的概率值 組成的列向量"""assert self.interception is not None and self.coef_ is not None,\"在predict之前请先fit"X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])return self._sigmoid( X_b.dot(self._theta) ) def predict(self, X_predict):""" 根據概率值是否大於0.5 進行分類 """proba = self.predict_proba(X_predict)return np.array(proba>=0.5,dtype='int')def score(self, X_test, y_test):y_predict = self.predict(X_test)return accuracy_score(y_test, y_predict)def __repr__(self):return "LogisticRegression()"
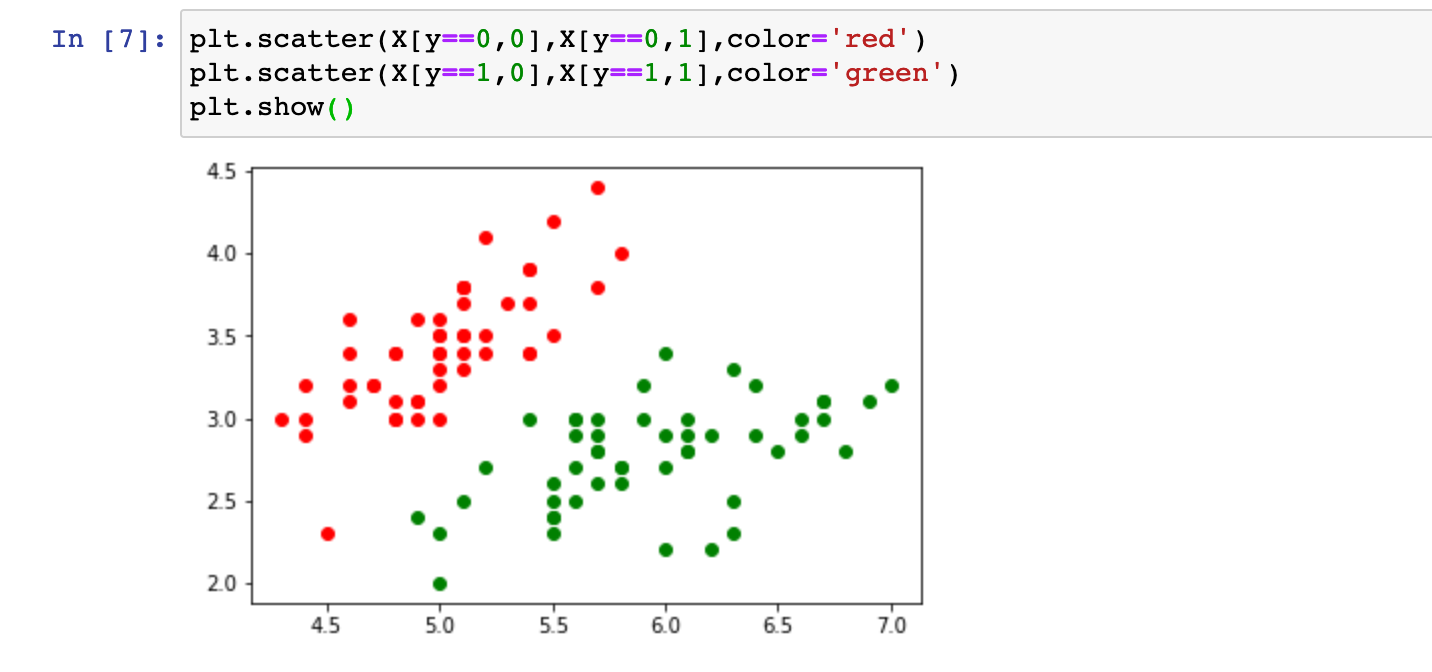
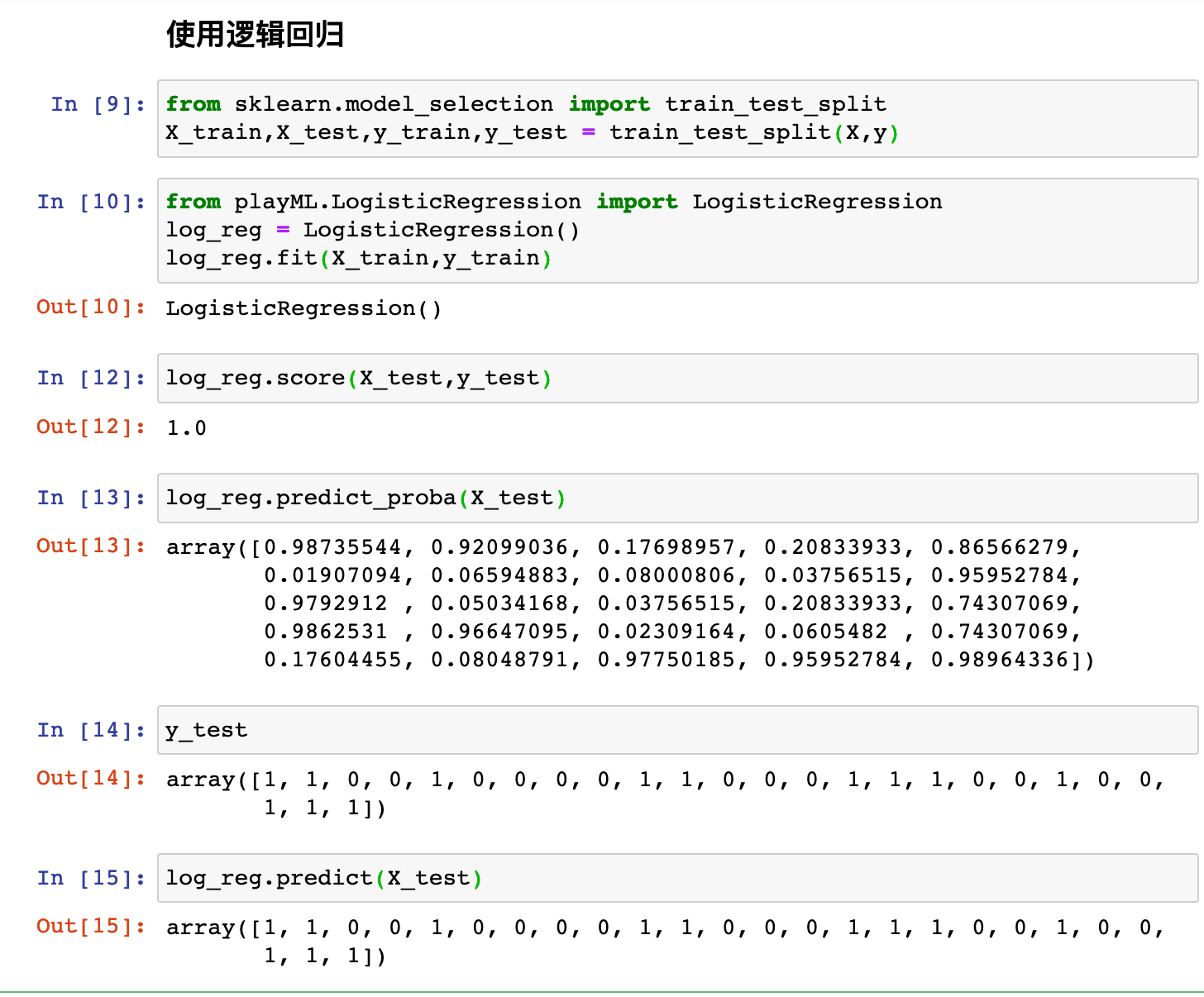
使用我们封装的逻辑回归算法:(使用鸢尾花数据集)

0x04 决策边界
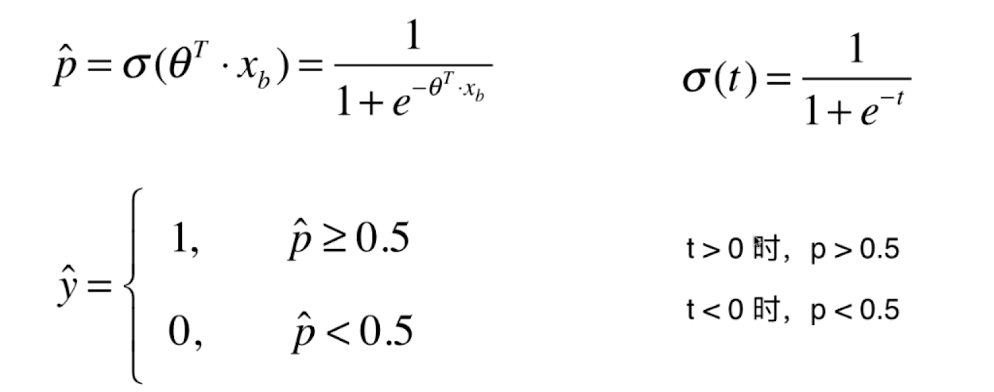
因为 t = theta.T.dot(Xb) 所以:
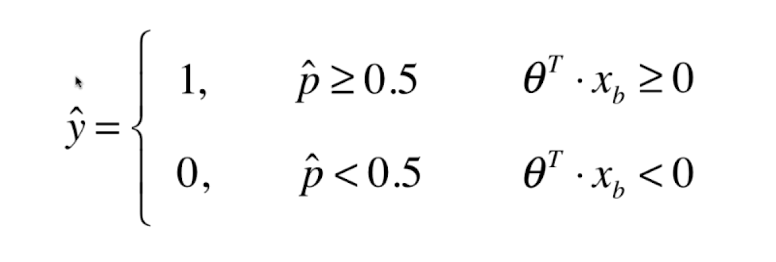
y_hat 到底是1还是0,取决于 theta.T.dot(Xb) 和0的关系,我们将theta.T.dot(Xb) =0 称为决策边界

也就是说决策边界 实际上就是我们通过逻辑回归训练出来的那条直线。
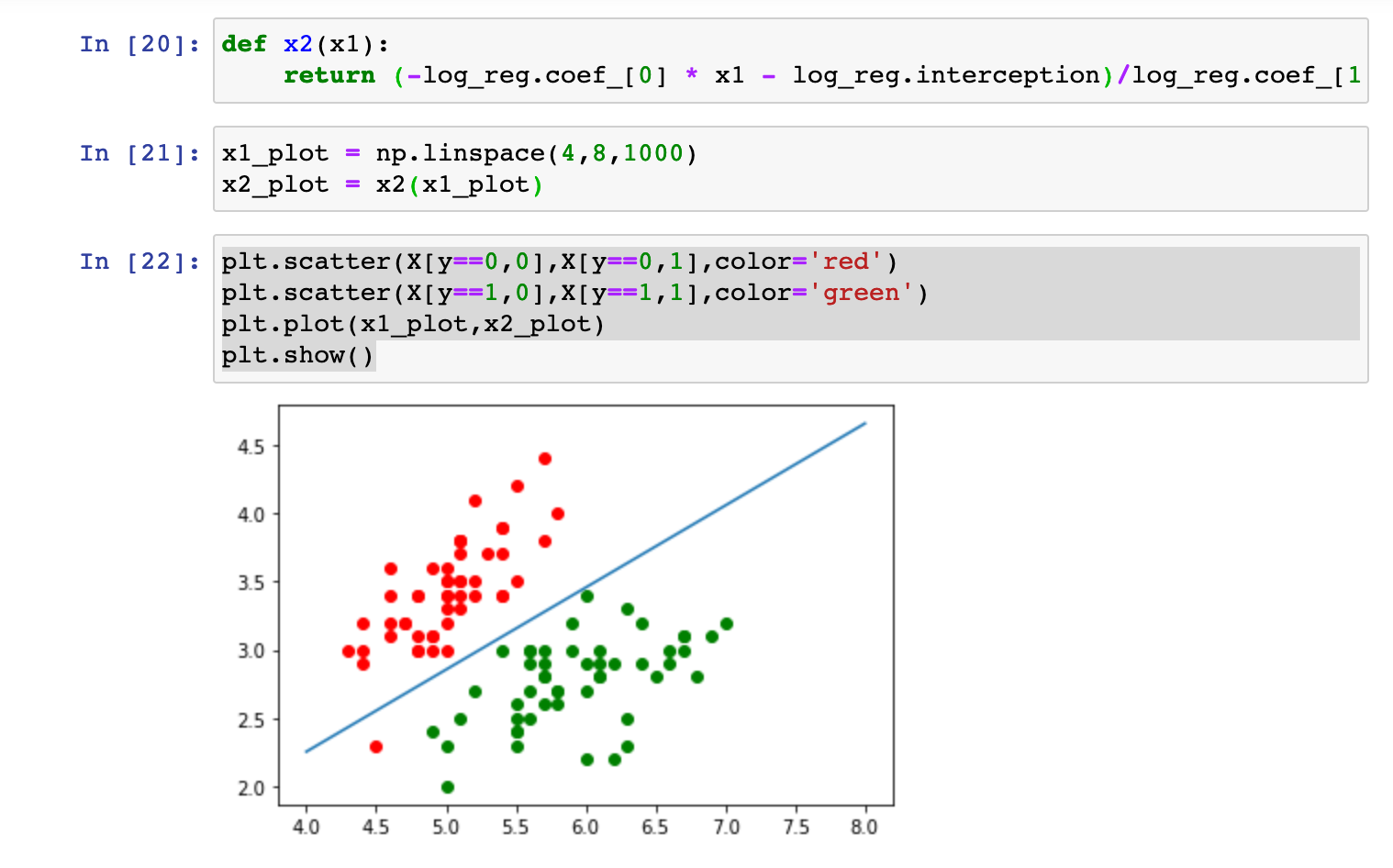
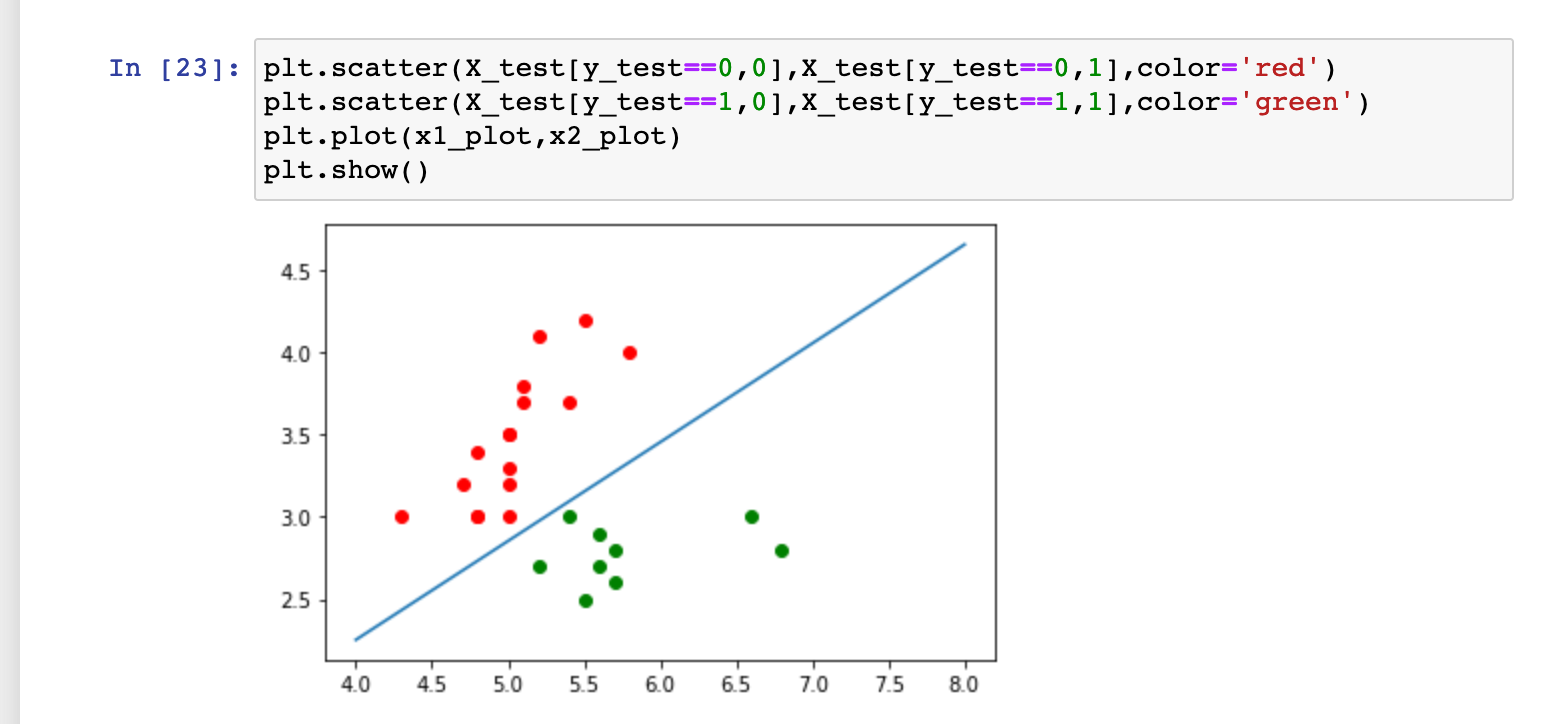
不规则的决策边界的绘制方法:
思路: 将x轴 和y轴 构成的平面 划分为许多个小点,对于这些小点都使用模型进行预测,得到一个分类值
那么我们根据不同分类值所占领的区域 就可以圈出决策边界
例如:

参考代码:(仅供参考)

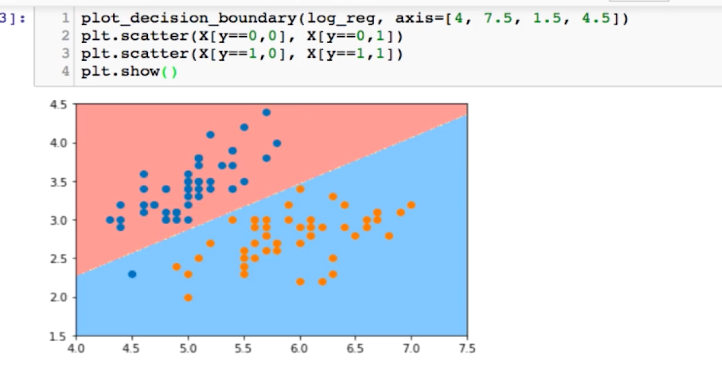
逻辑回归算法中实际是将决策边界的表达式直接求出来了,但是knn算法中是没有这个表达式的,我们可以按照上述将平面划分为许多个点的思路就求下kNN算法的决策边界
例如:只考虑两类鸢尾花
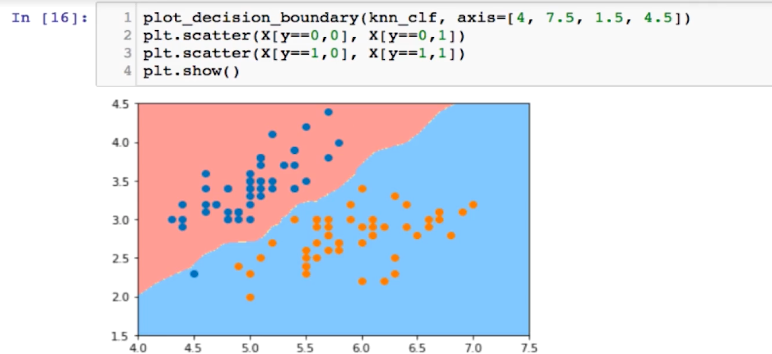
考虑三类鸢尾花,决策边界非常弯曲,是过拟合的征兆
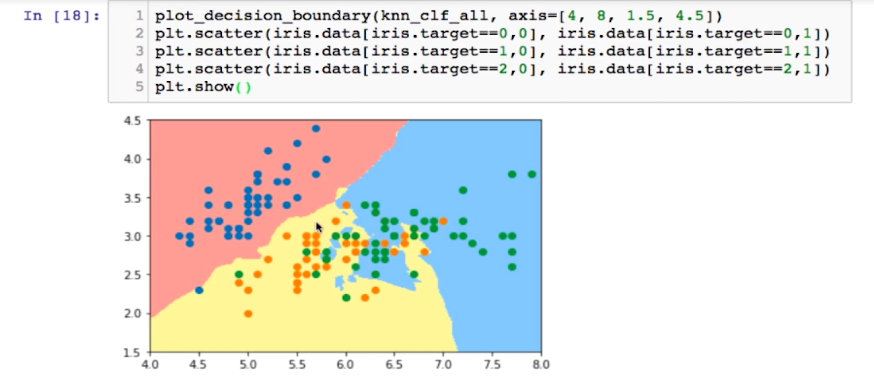
将k的值变大,模型变得更加简单,重新绘图:
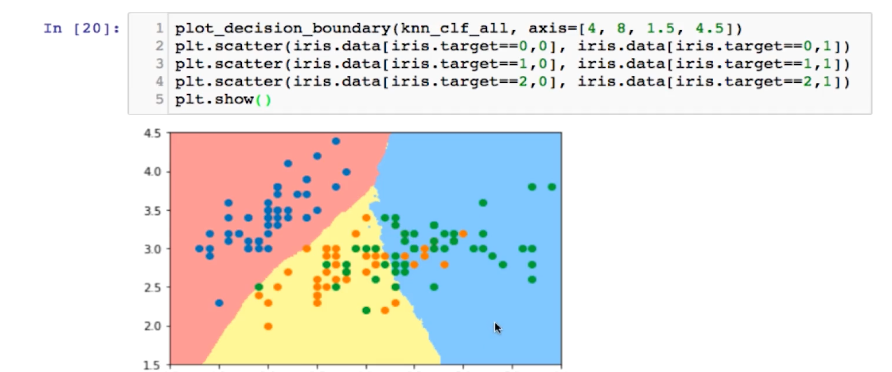
0x05 逻辑回归中使用多项式特征
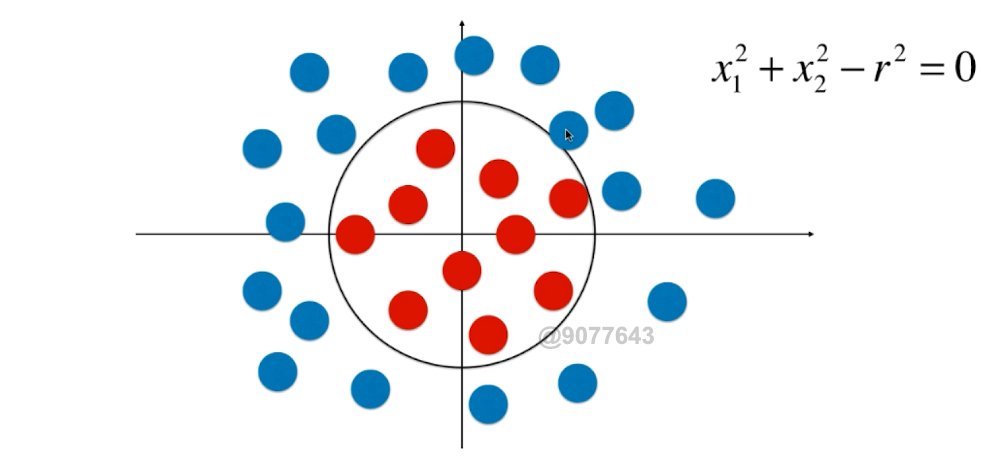
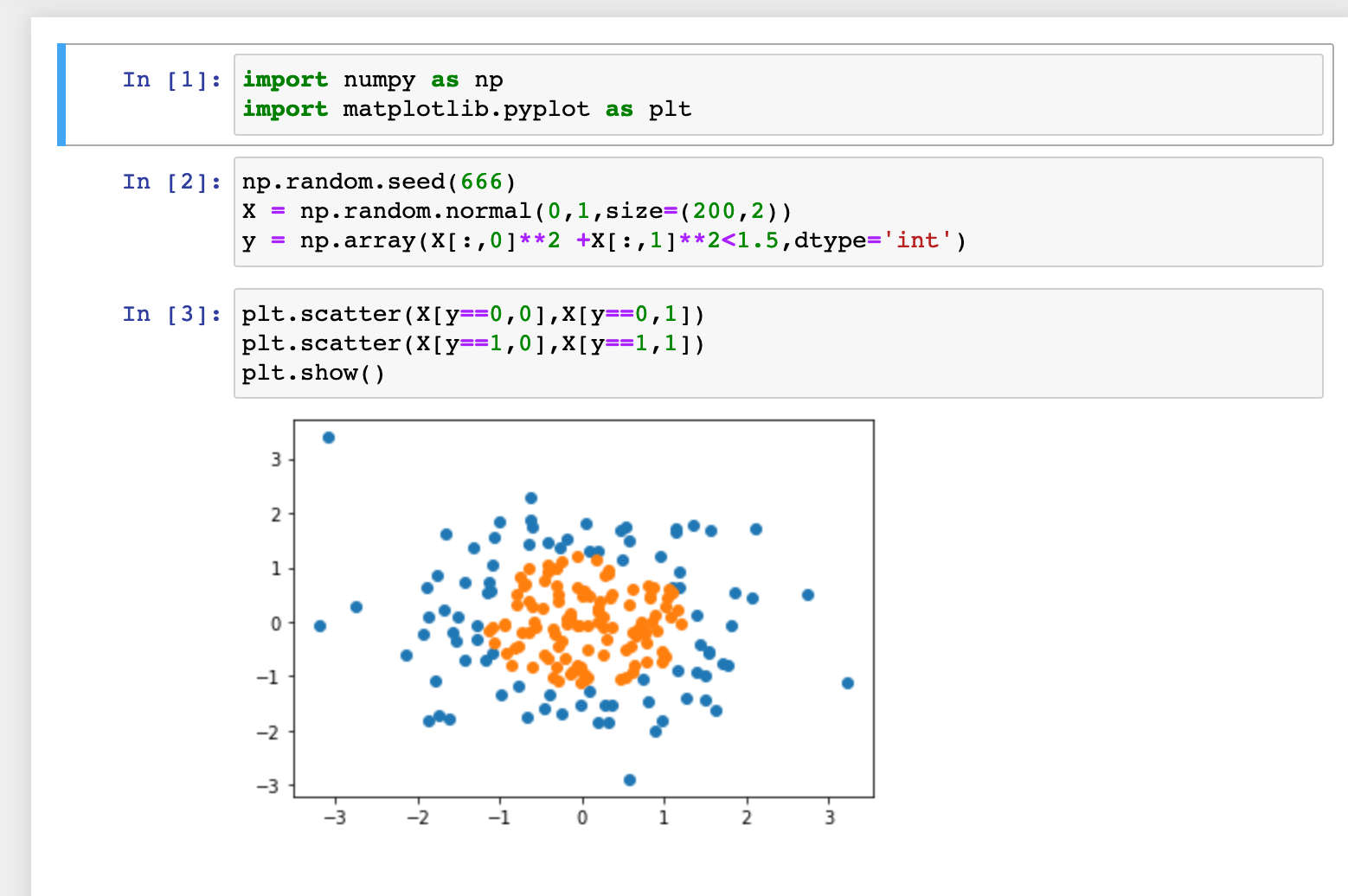
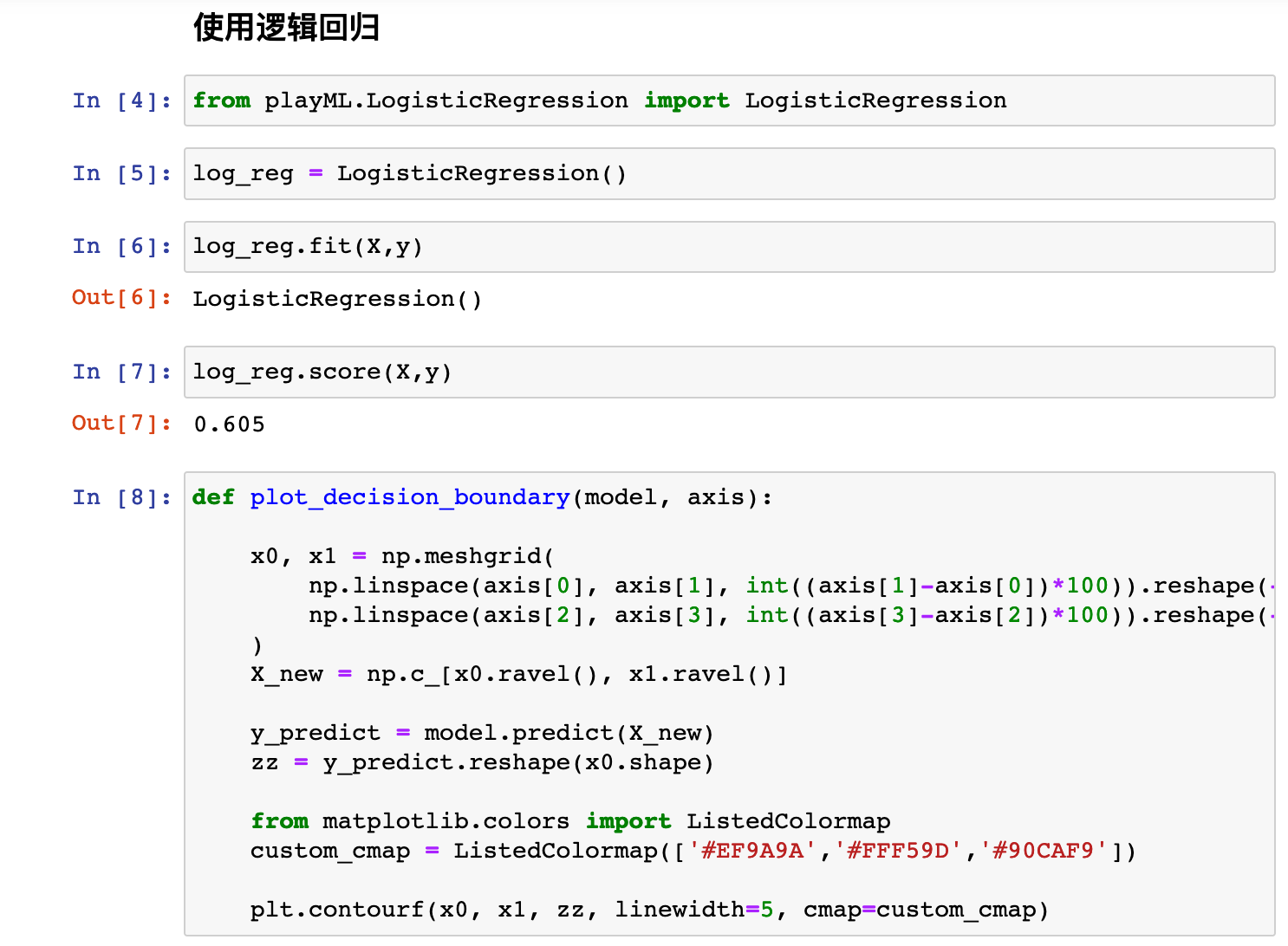
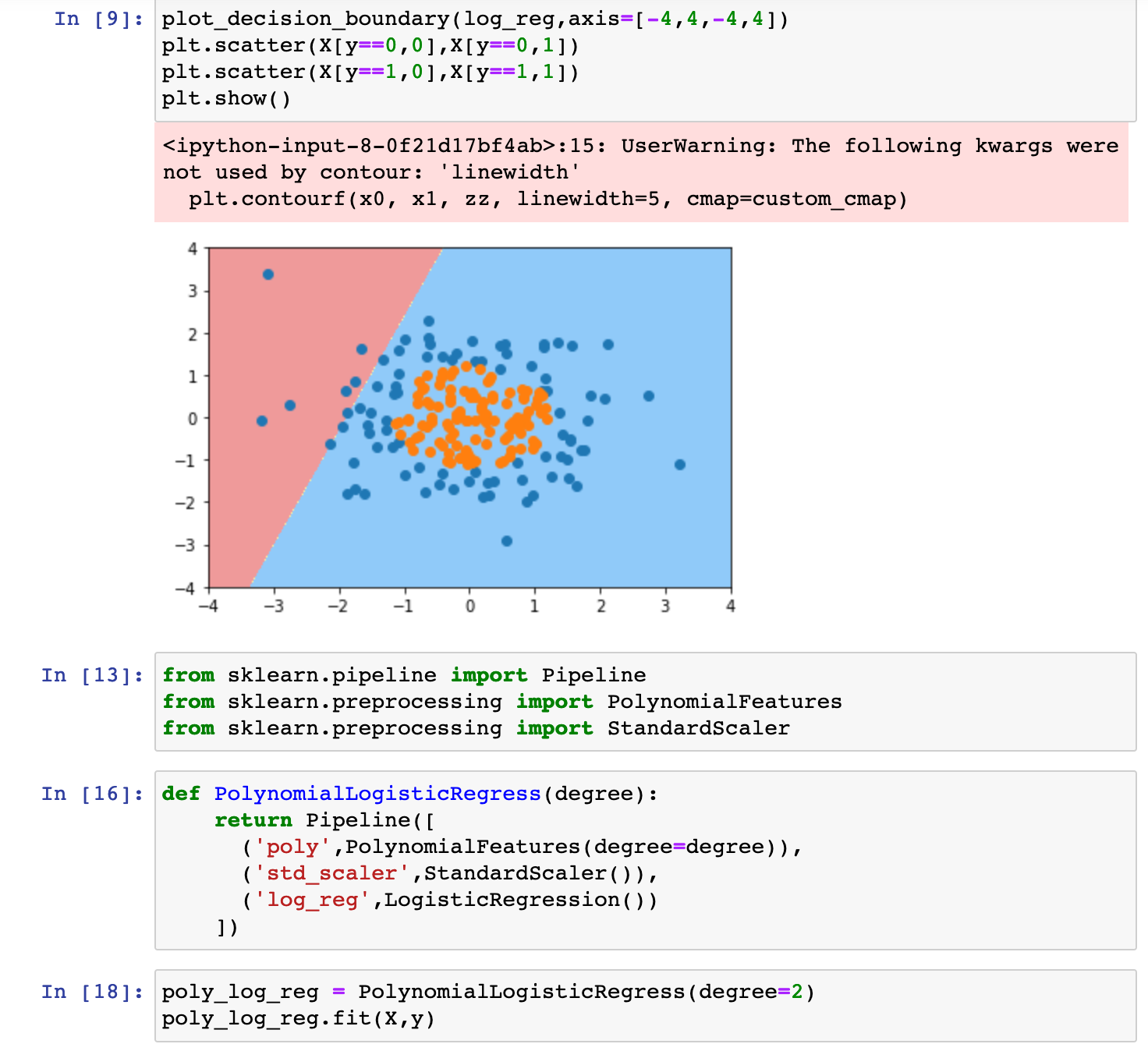
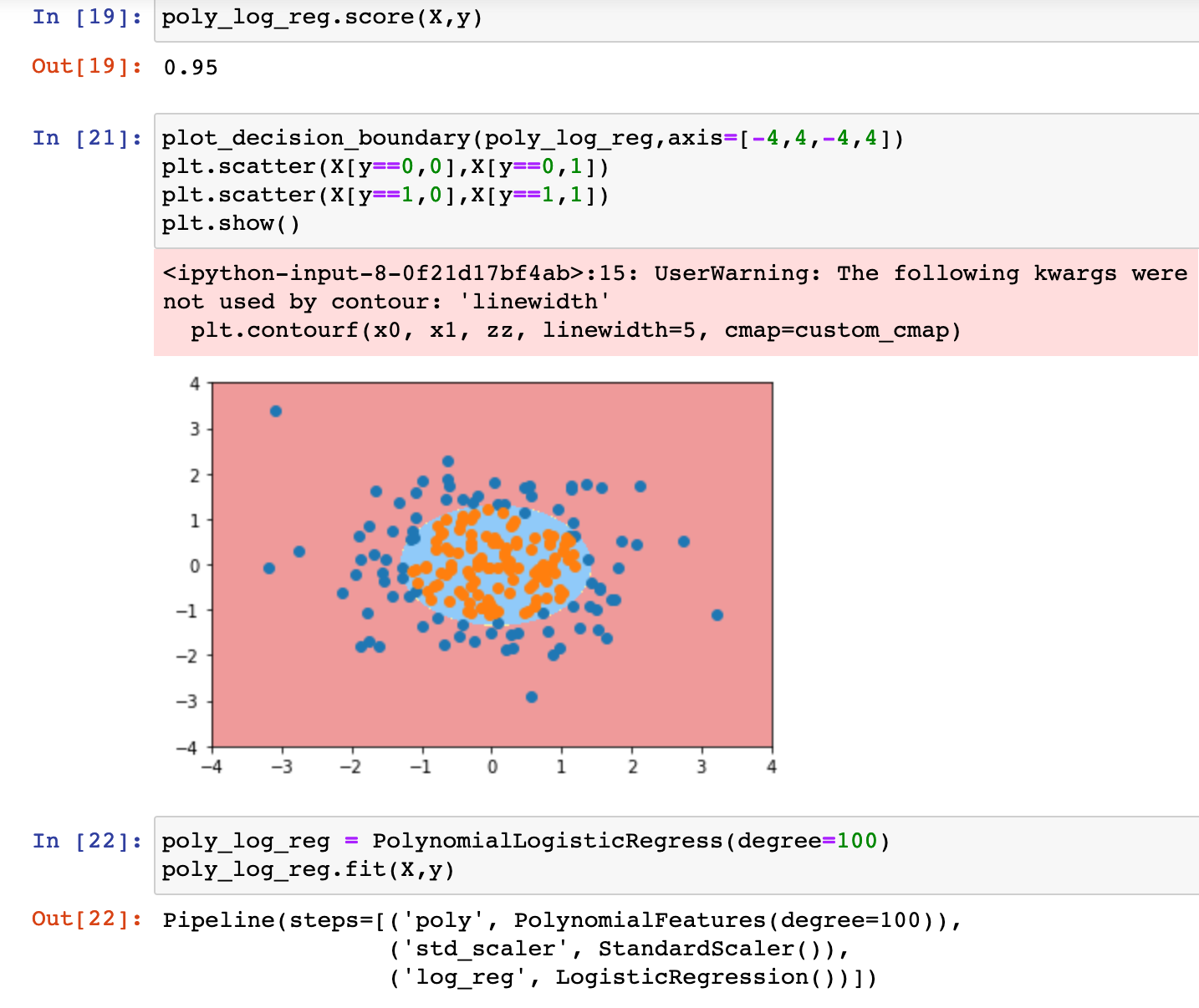
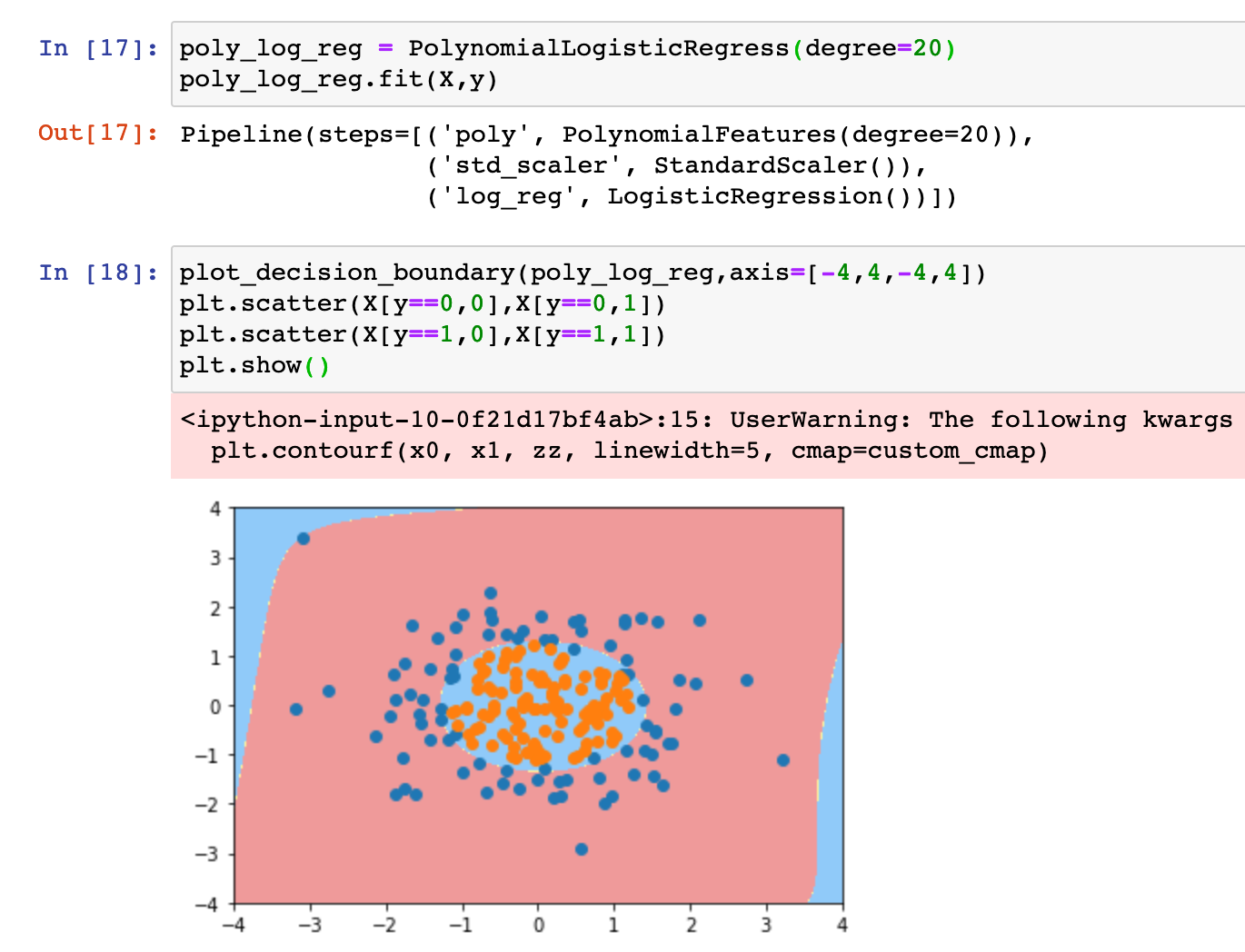
0x06 scikit-learn中的逻辑回归
对正则化的过程进行改进:
添加一个大C,用来配置正则项L的比重

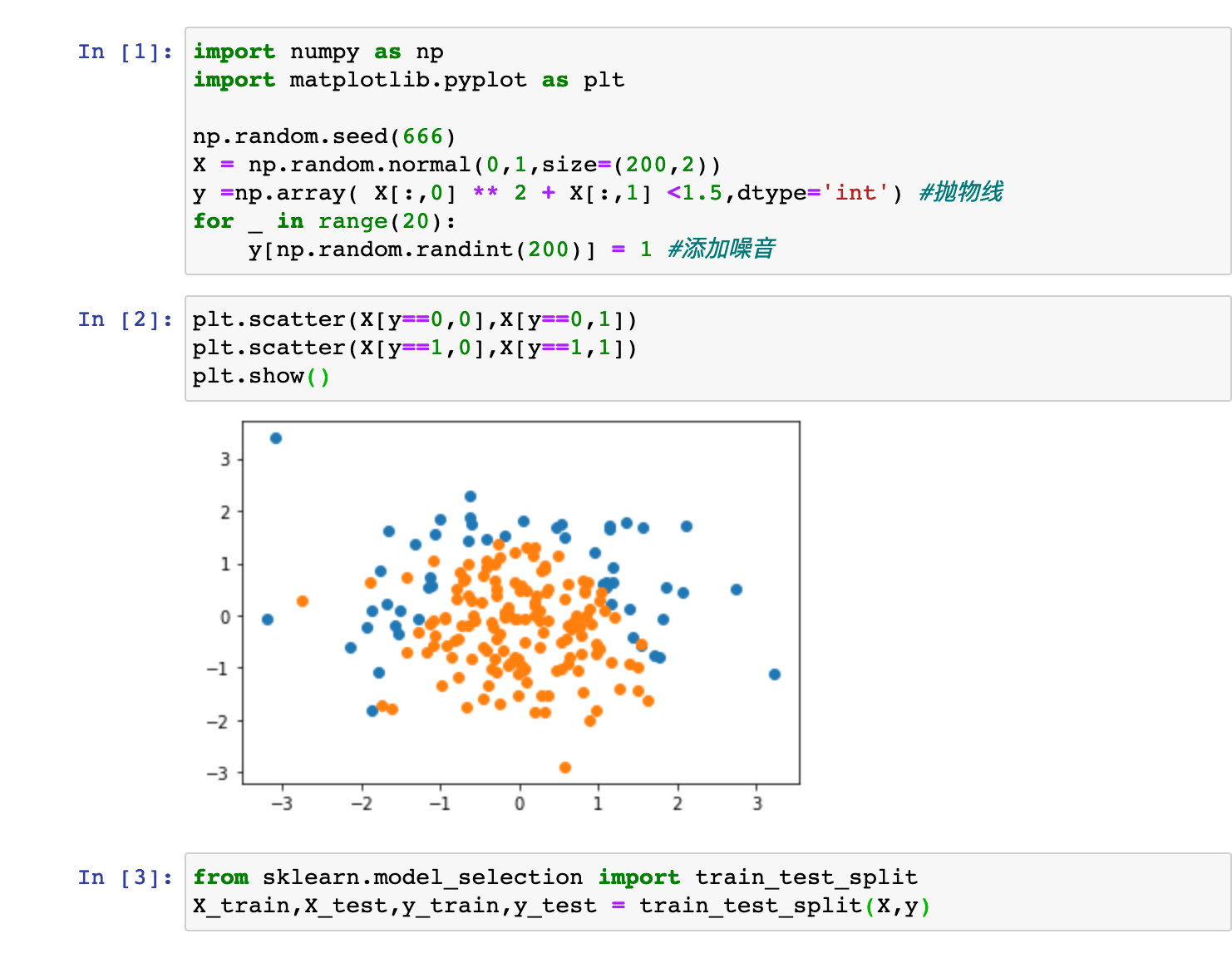
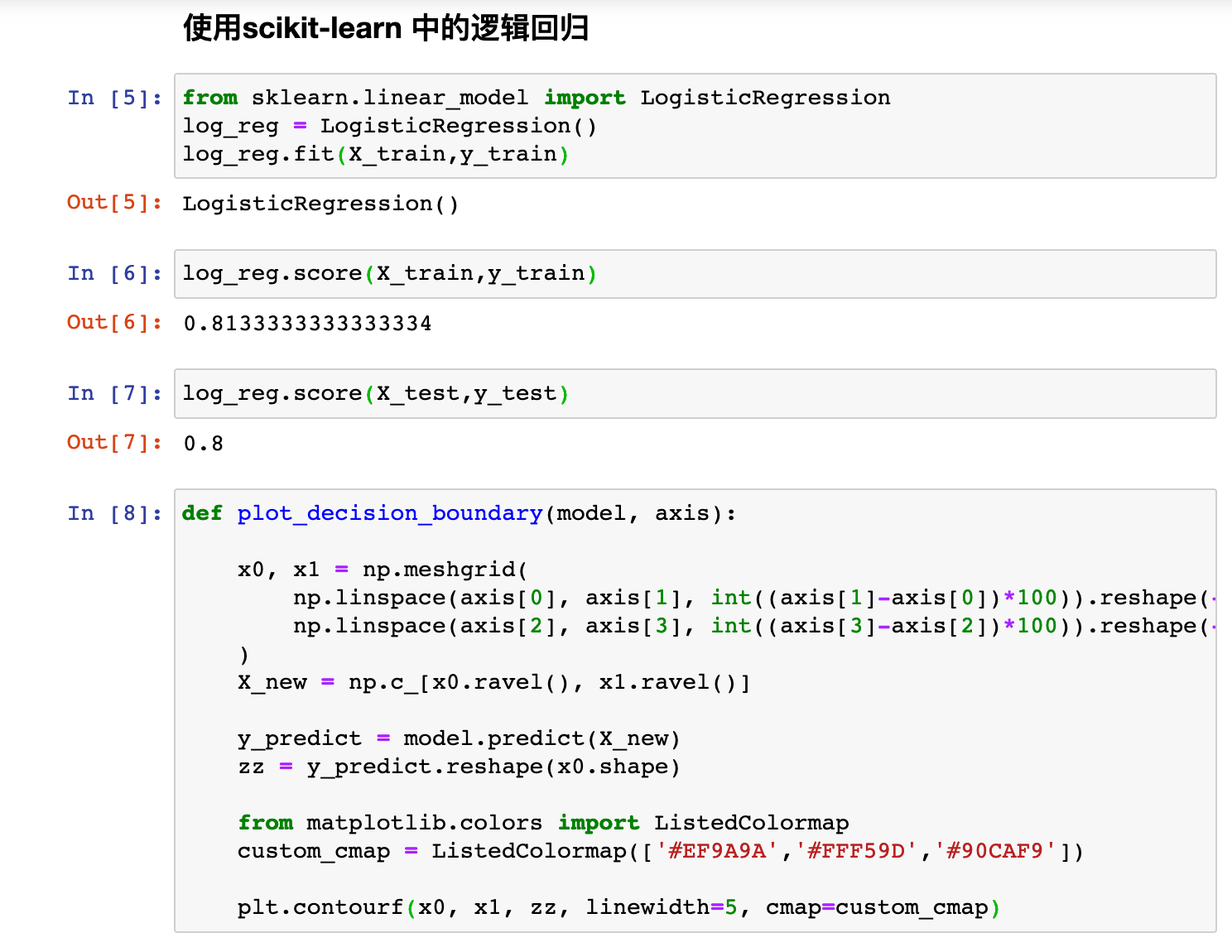
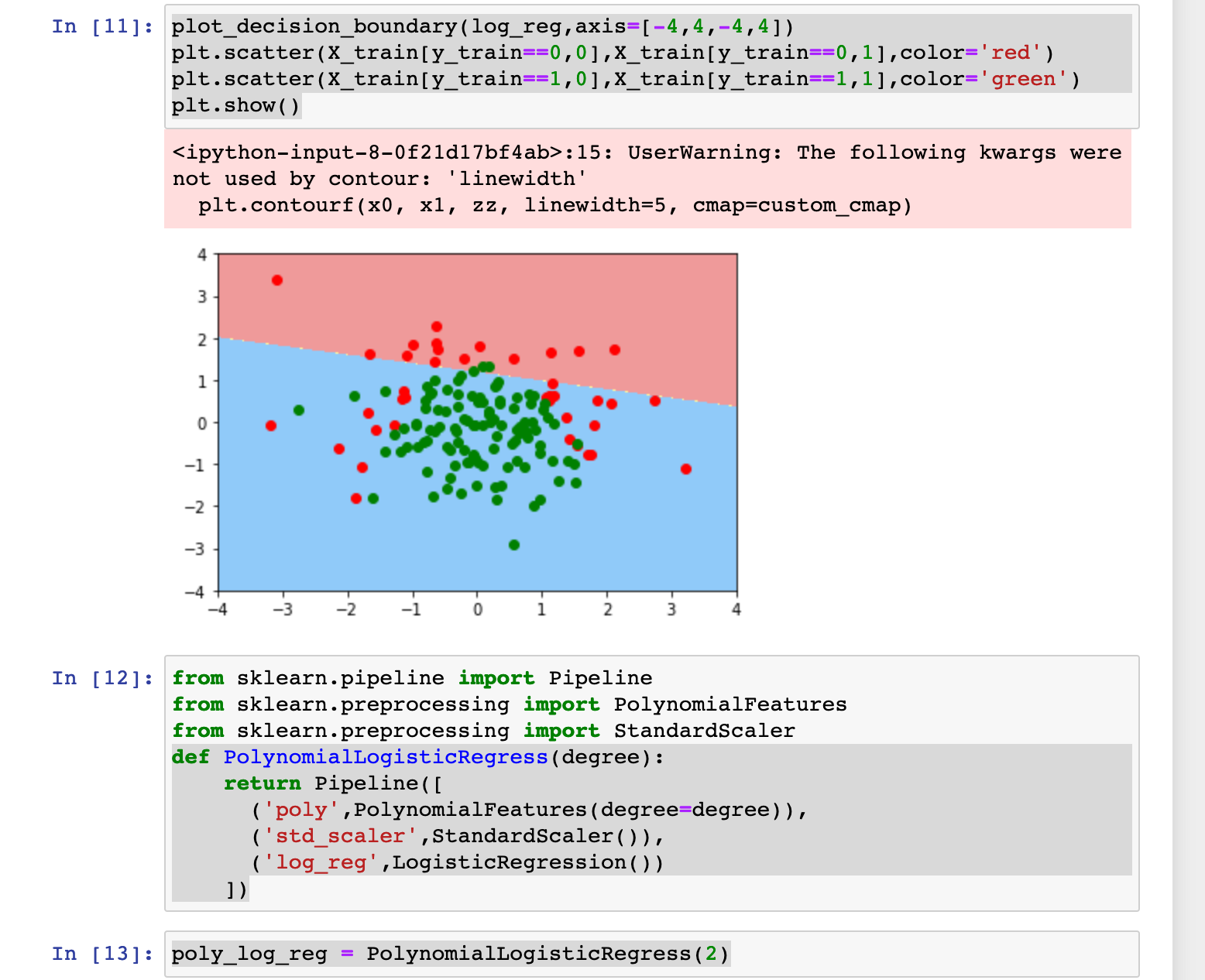
编程实践:
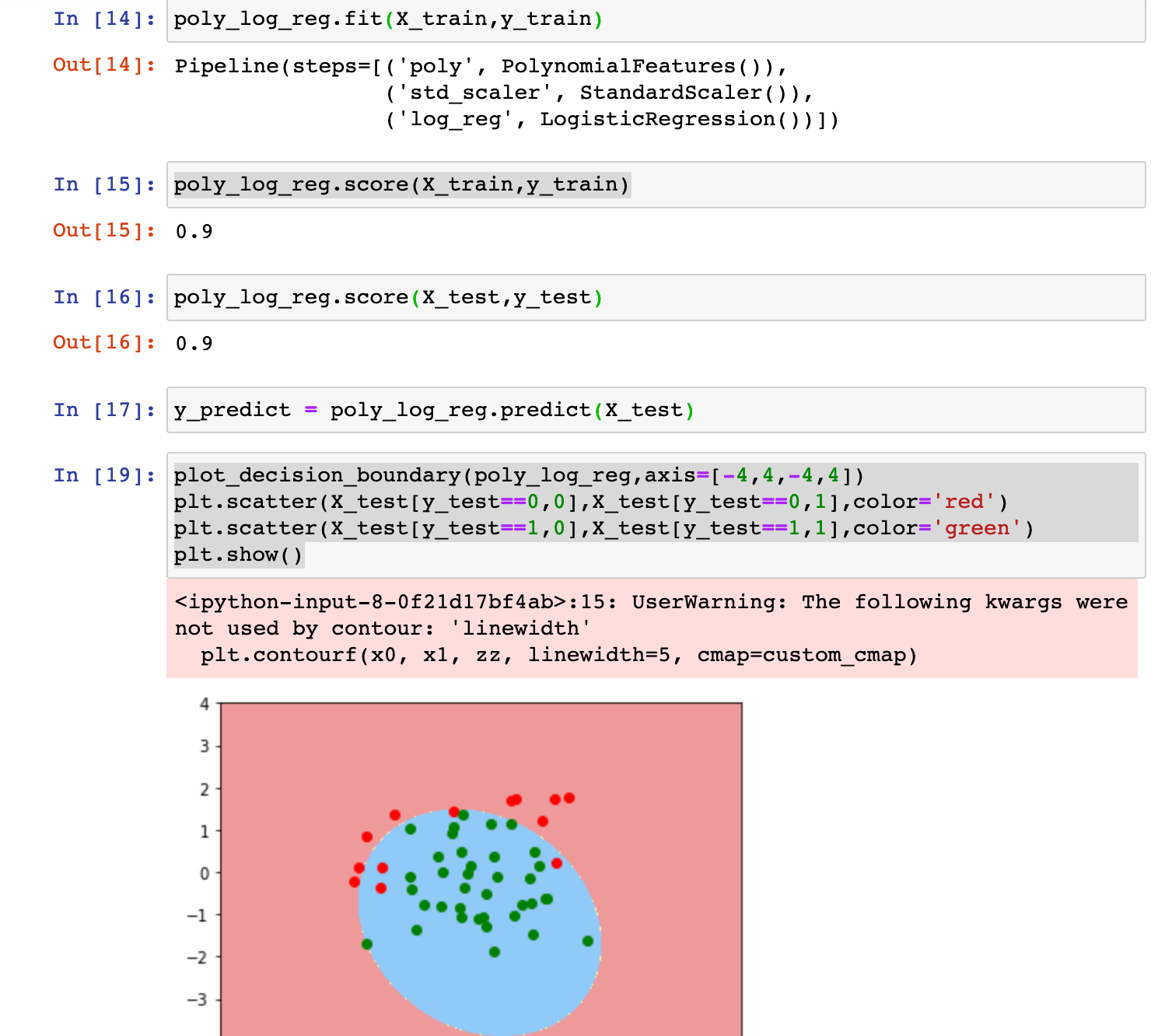
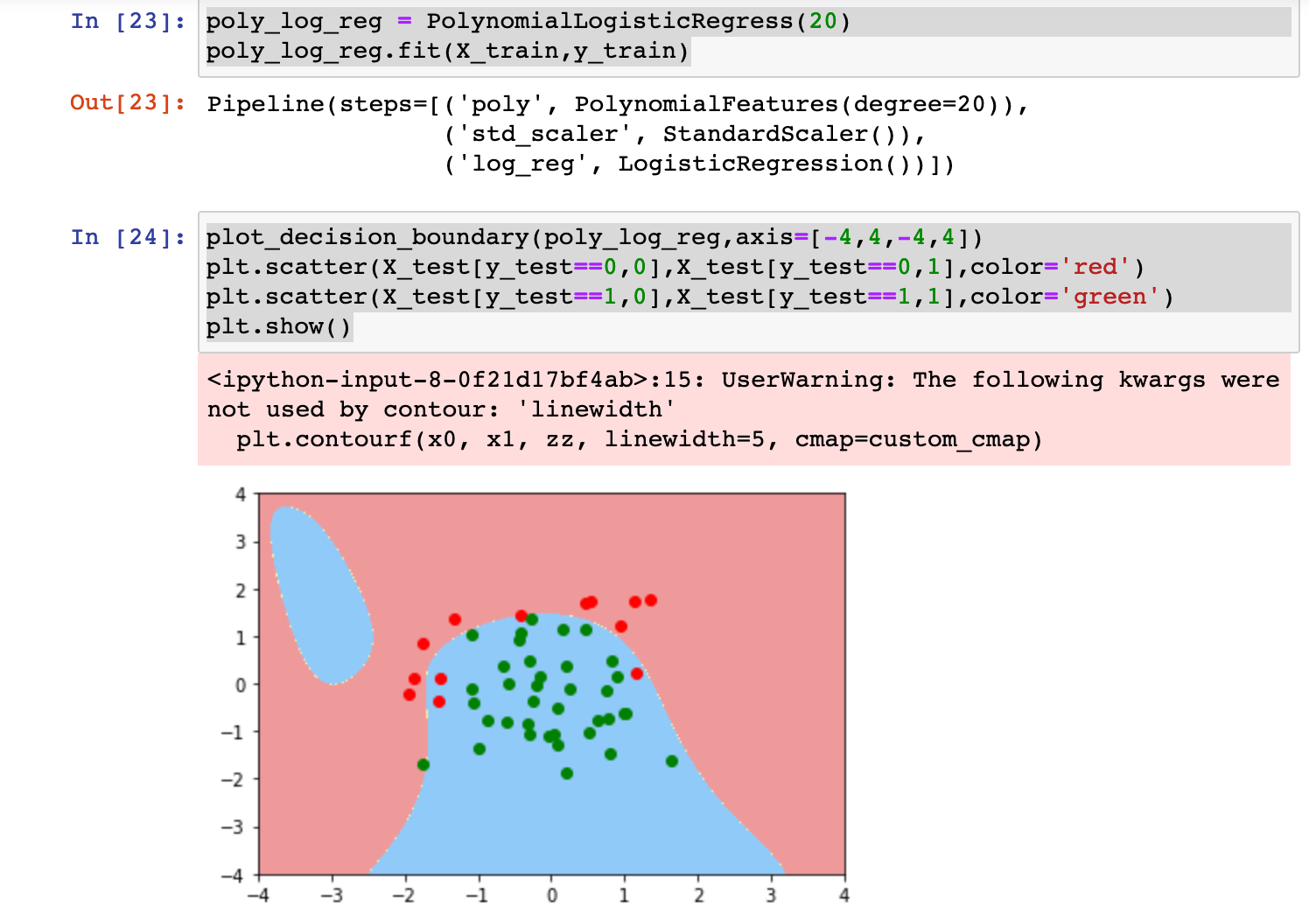
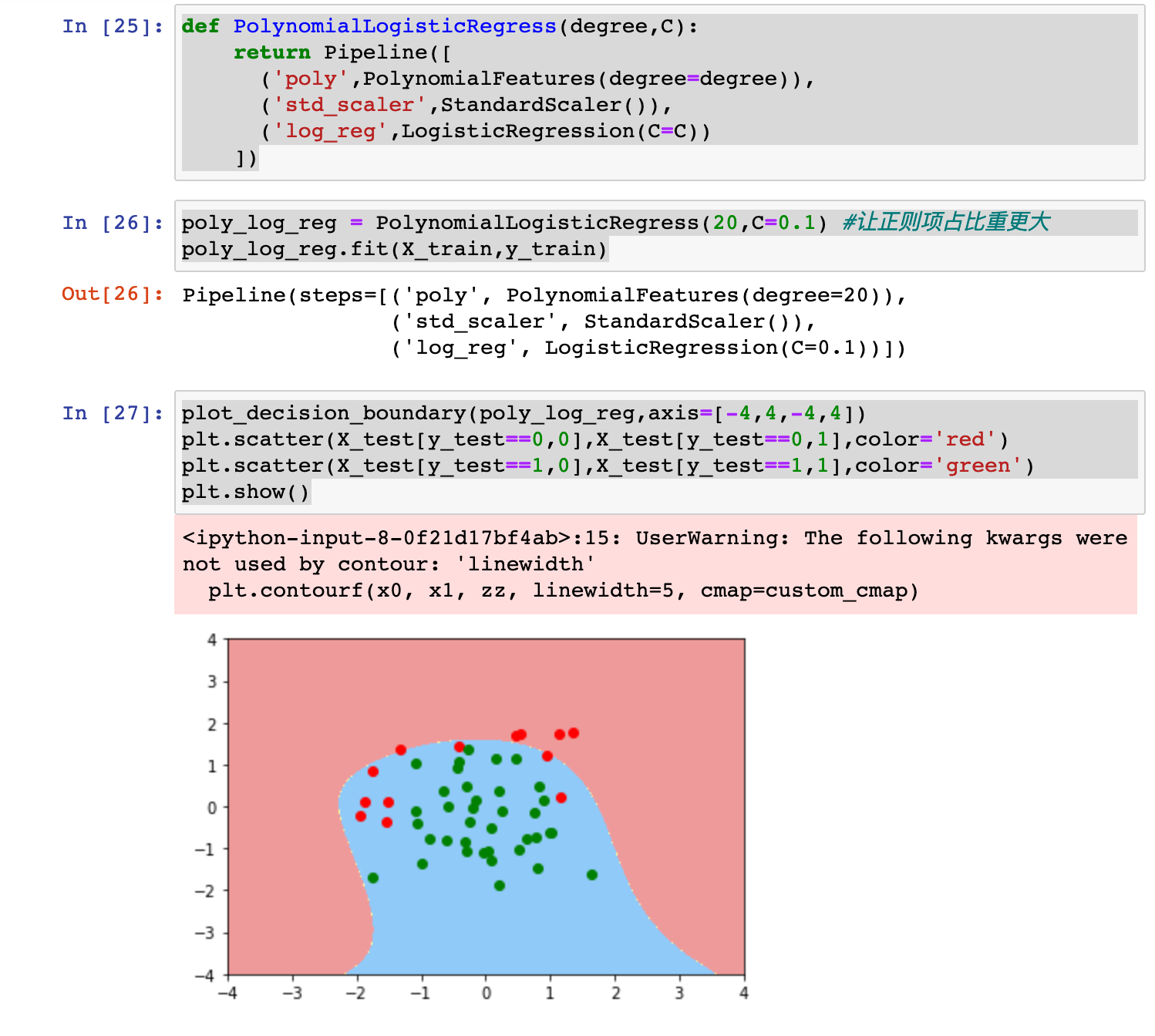

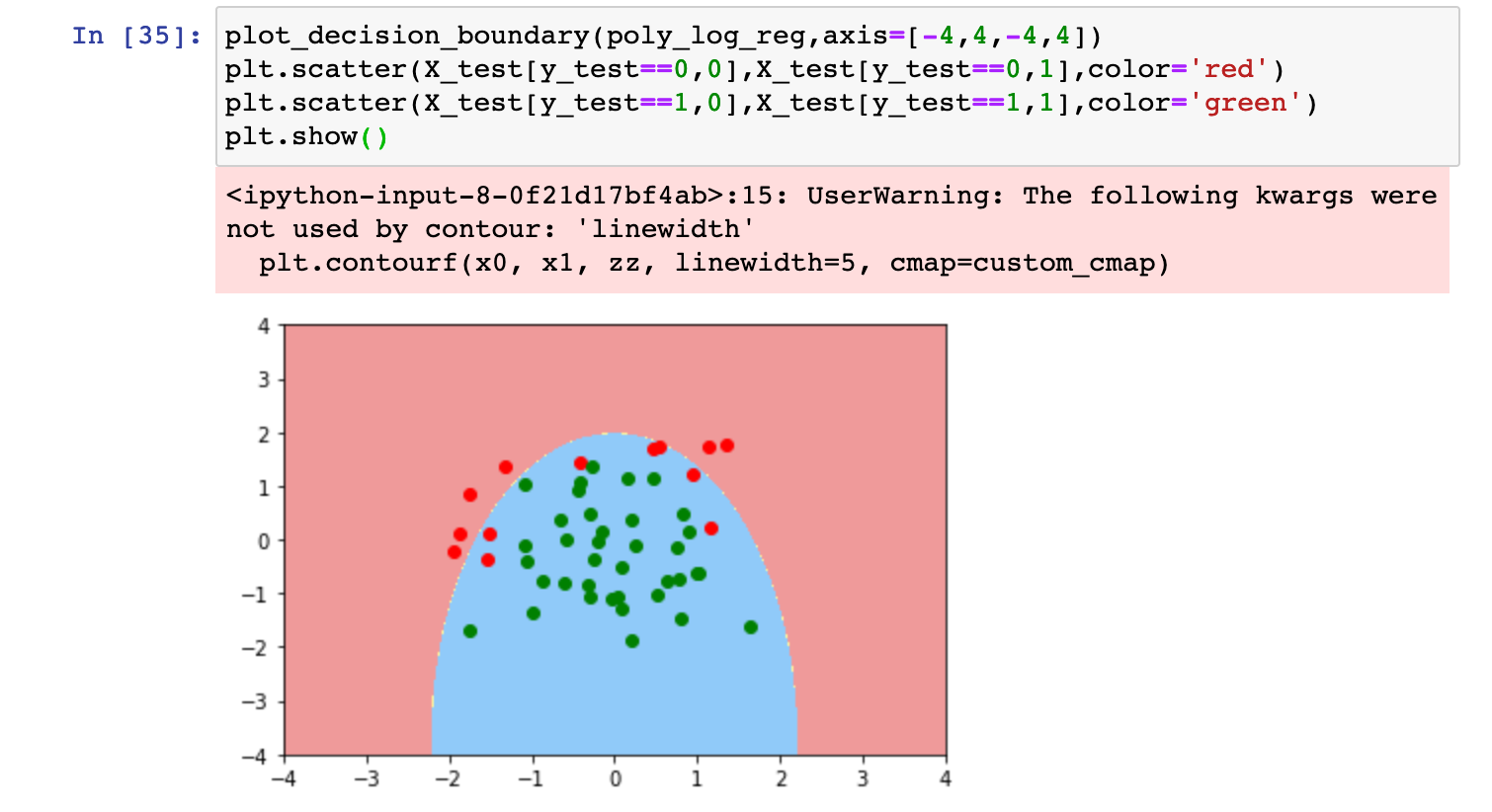
0x07 OvR与OvO
我们之前说逻辑回归只能解决二分类问题,但是有两种改造方案可以让逻辑回归解决多分类问题:
OvR 和OvO
#OvR (One vs Rest)一针对剩余
比如我们现在有一个四分类问题,我们可以将这个四分类问题转化为四个二分类问题:
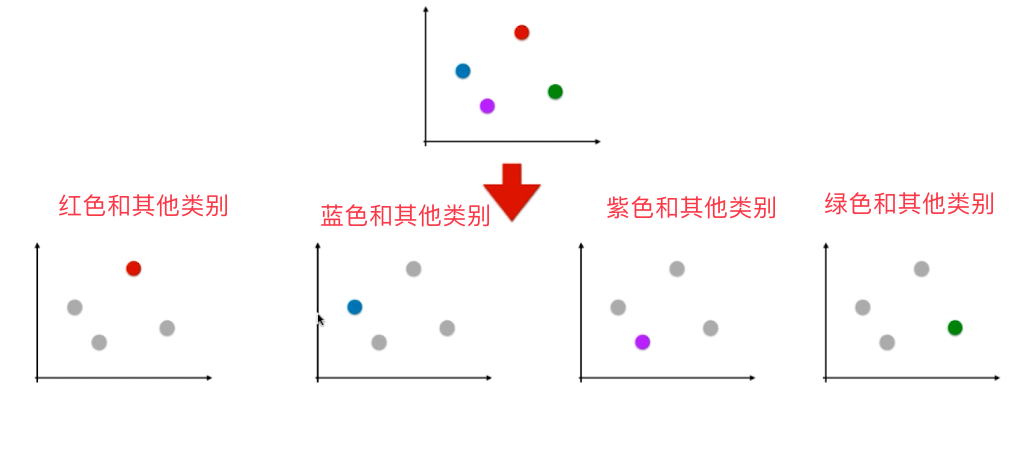
#OvO (One vs One)一对一
比如我们现在有一个四分类问题,我们从中取两个类别,直接判断新来的样本点是这两个类别中某一个的概率
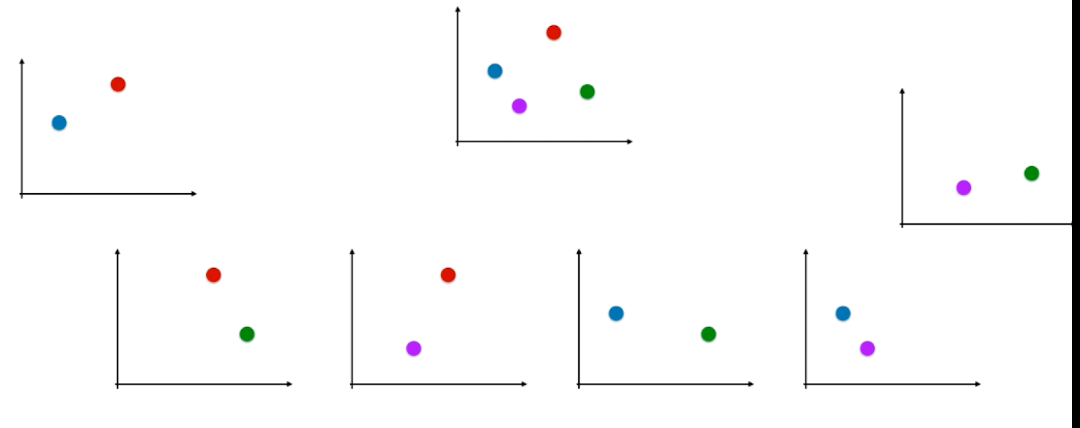
将一个四分类问题 归约为六个二分类问题。
![]()
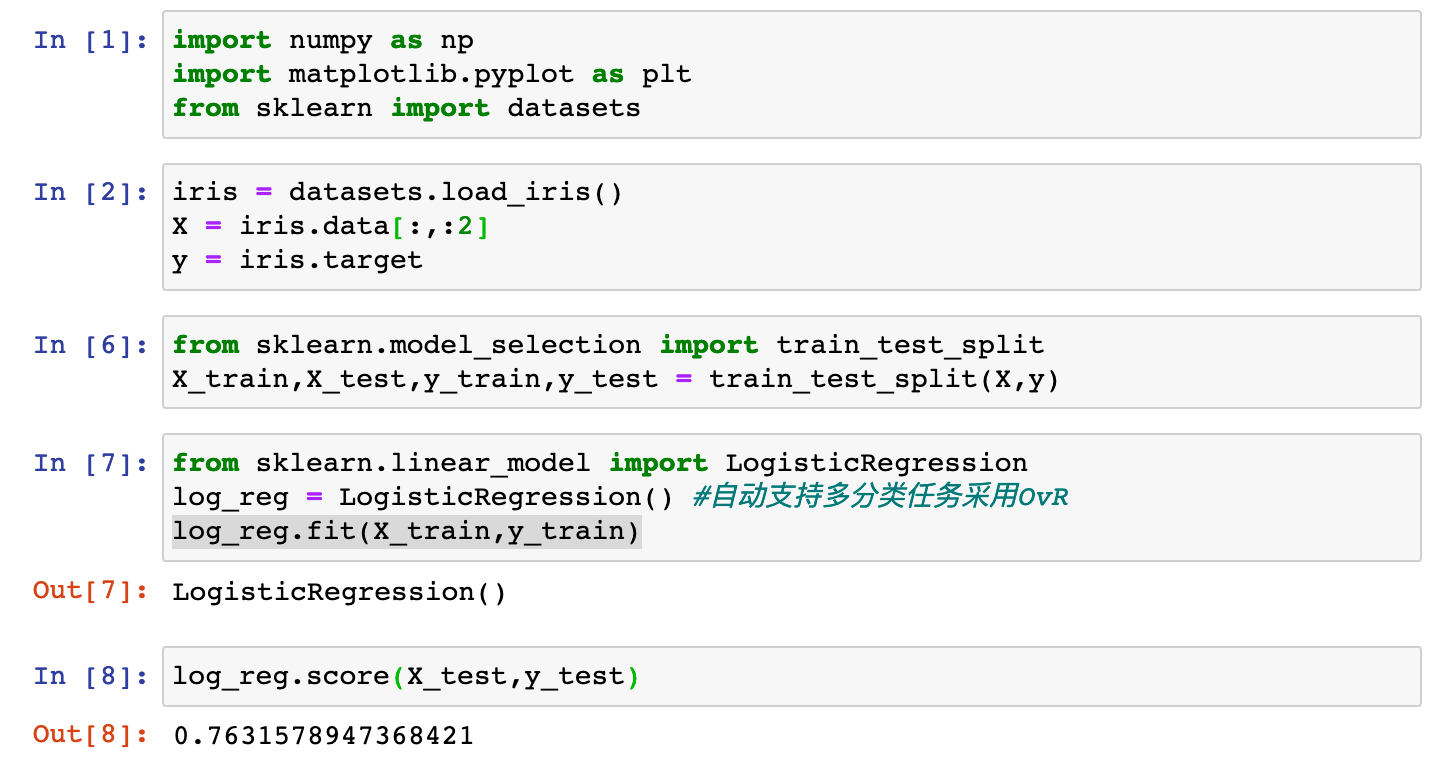
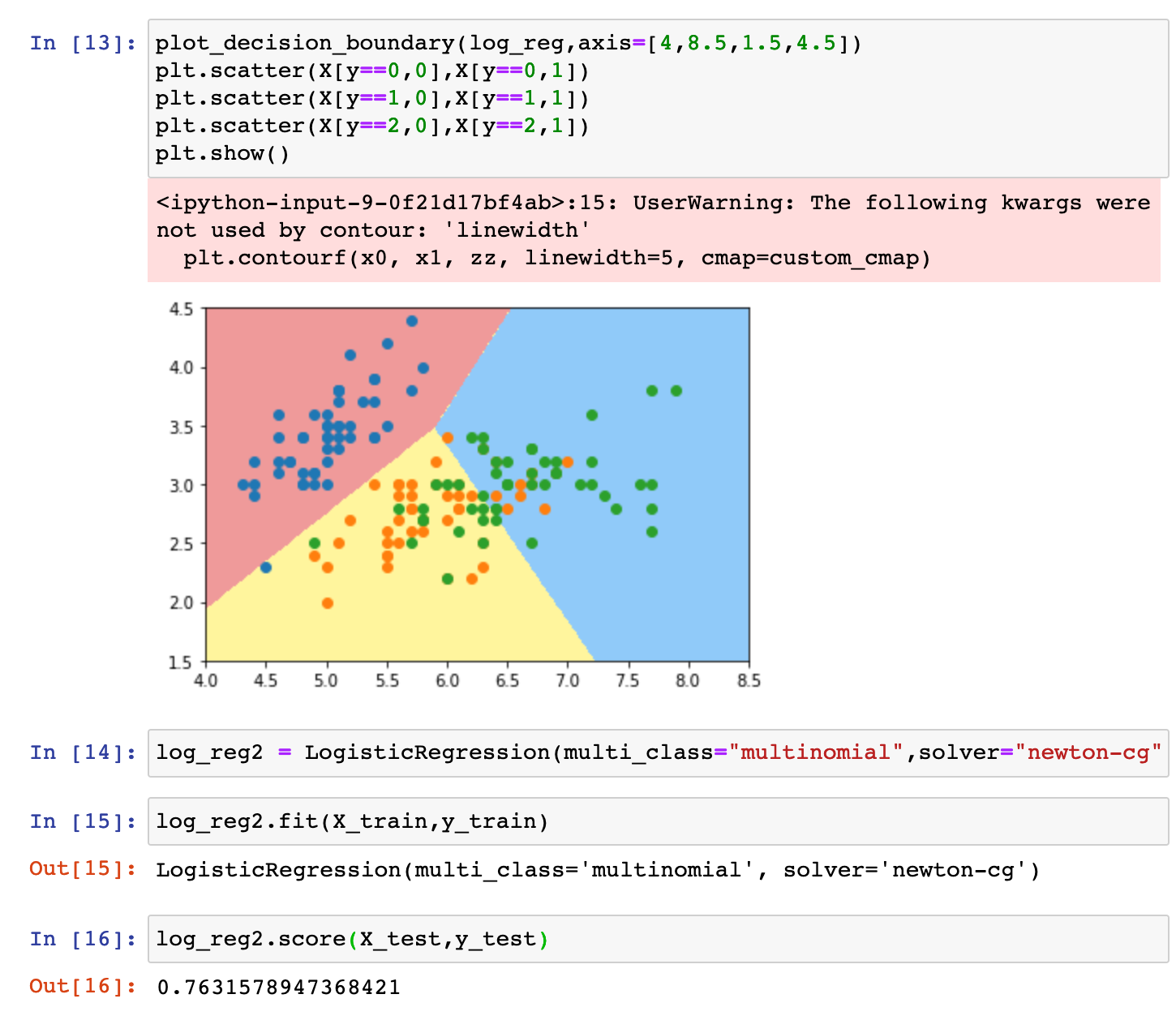
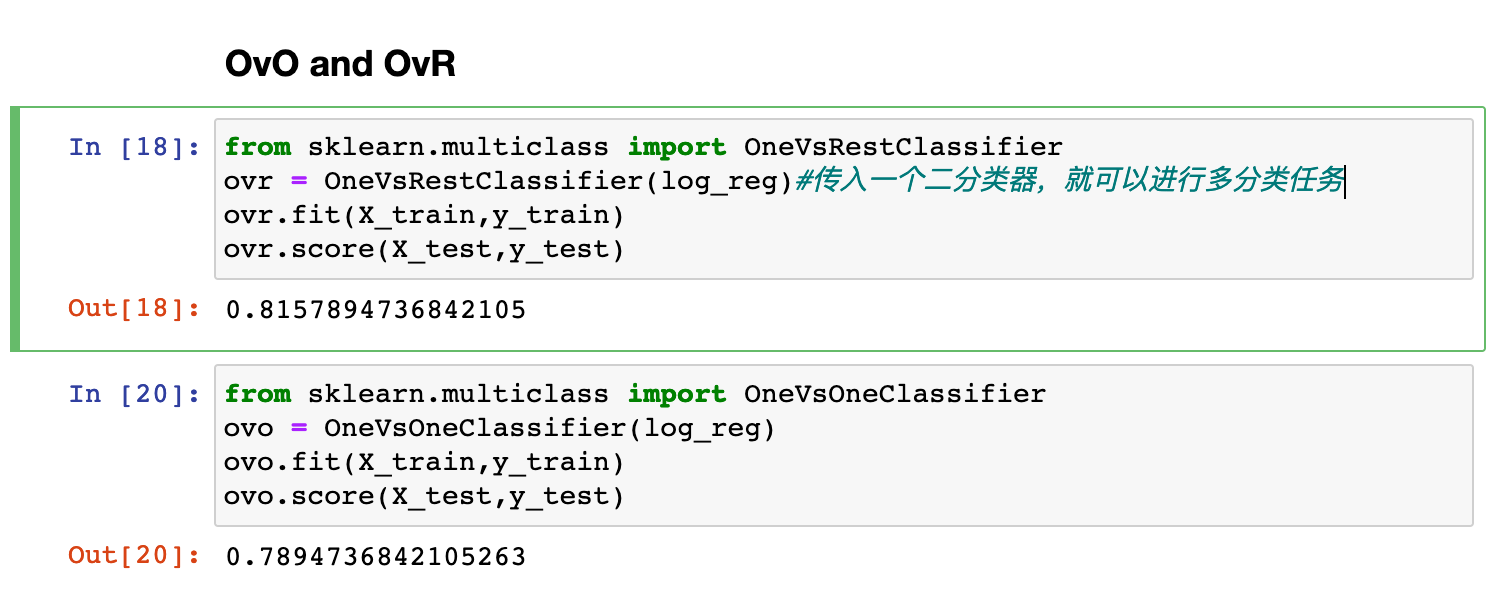
编程实践:

上一篇:IDEA中常见的英文名词简明解释
下一篇:javaweb高校运动会管理系统