【人工智能】—Admissible Heuristics可容许启发式函数

• 如何选择启发式函数
• 如何评价启发式函数
• 松弛操作
• 评价函数f(n)

如何选择启发式函数

• 对8数码问题来说：
  • h1(n)h_1(n)h1​(n) = number of misplaced tiles(错位的棋子数)
  • h2(n)h_2(n)h2​(n) = total Manhattan distance(所有棋子到其目标位置的水平竖直距离和)
    (i.e., no. of squares from desired location of each tile
  • 如下起始状态与结束状态
    
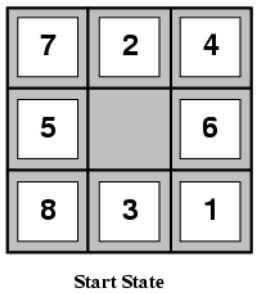
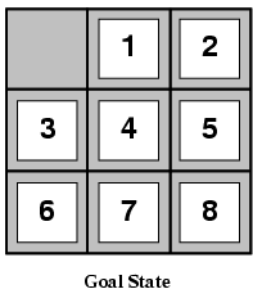
  • 在上述两个启发式函数下，对到达目标状态的估计耗散为：h1(S)=8h_1(S)= 8h1​(S)=8
    h2(S)=3+1+2+2+2+3+3+2=18h_2(S) = 3+1+2+2+2+3+3+2 = 18h2​(S)=3+1+2+2+2+3+3+2=18

如何评价启发式函数

• If h2(n)≥h1(n)h_2(n) ≥ h_1(n)h2​(n)≥h1​(n)for all n (both admissible)
• then h2h_2h2​ dominates h1h_1h1​ (dominate 统治、占优)即h2h_2h2​ 优于h1h_1h1​
• h2h_2h2​ is better for search
• 典型的搜索成本(扩展的平均节点数)：
• d=12
  • IDS = 3,644,035 nodes(迭代加深深度优先搜索)
  • A∗(h1)A^*(h_1)A∗(h1​) = 227 nodes
  • A∗(h2)A^*(h_2)A∗(h2​) = 73 nodes
• d=24
  • IDS = too many nodes
  • A∗(h1)A^*(h_1)A∗(h1​)= 39,135 nodes
  • A∗(h2)A^*(h_2)A∗(h2​) = 1,641 nodes
• 给定任何可容许的启发函数ha，hbh_a，h_bha​，hb​h(n)=max(ha(n)；hb(n))h(n)=max(h_a(n)；h_b(n))h(n)=max(ha​(n)；hb​(n))
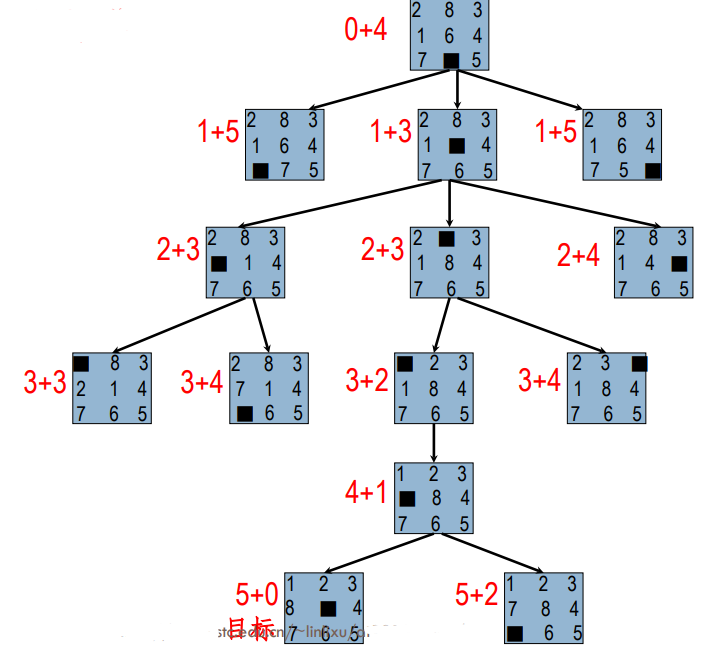
  也是可容许的并且dominatesha，hbh_a，h_bha​，hb​
• 使用 评价函数f(n)=g(n)+h(n)f(n) = g(n) +h(n)f(n)=g(n)+h(n)搜索
  • h(n)=错放数字个数
  • g(n) = 节点深度
  • 结果如下：

松弛操作

• 有些复杂问题不能像上面一样直观的得到启发函数，此时就要考虑松弛操作
• 如下移动三角至目标位置
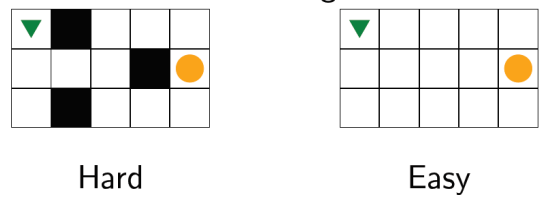
• 这里在有障碍物的情况下，很难得到一个满足要求(预估耗散永远不会大于实际耗散)启发式函数，因此在这里考虑一个更简单情况，使用更简单情况下的实际耗散作为启发式函数，这样就可以保证估计耗散不会大于实际耗散，启发式函数采用起点到终点的曼哈顿距离
  因此，这里可以将松弛操作理解为去除问题中的部分约束、限制
• 构造松弛问题
  • 原问题：一个棋子可以从方格A移动到方格B，如果A与B水平或者垂直相邻而且B是空的
  • 松弛1：一个棋子可以从方格A移动到方格B，如果A与B相邻 — h2
  • 松弛2：一个棋子可以从方格A移动到方格B，如果B是空的
  • 松弛3：一个棋子可以从方格A移动到方格B —h1
• 如果有一个可采纳启发式的集合h1,…,hm{h_1 ,…, h_m }h1​,…,hm​
  h(n)=max(h1(n),…,hm(n))h(n) = max(h_1(n),…, h_m(n))h(n)=max(h1​(n),…,hm​(n))可采纳并比成员启发式更有优势

评价函数f(n)

• h(n) — heuristic, estimate of cost from n to the closest goal
  （节点n到目标节点的最低耗散路径的耗散估计值）
• g(n) — path cost to n （初始节点到这个节点的路径损耗的总和）
• Possible evaluation functions: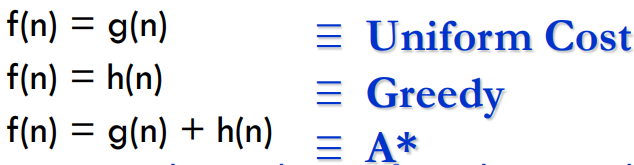估计通过节点n的解决方案路径的总成本