非线性系统的反馈线性化
仿射非线性或非仿射非线性指对输入是否是线性的。例如,系统能够写成 x′=f(x)+g(x)ux'= f(x) + g(x)ux′=f(x)+g(x)u 的形式,而不是 x′=f(x)+g(x)u2x'= f(x) + g(x)u^2x′=f(x)+g(x)u2,或者 x′=f(x,u)x'= f(x,u)x′=f(x,u) 中提不出 uuu,如果能提出一个 uuu 就是仿射非线性,否则就是非仿射非线性。
本文只涉及单输入单输出的仿射非线性系统,但有多个状态。
相对阶
对系统
x⃗′=f⃗(x⃗)+g⃗(x⃗)uy=h⃗(x⃗)\begin{aligned} & \vec{x}'= \vec{f}(\vec{x}) + \vec{g}(\vec{x})u \\ & y = \vec{h}(\vec{x}) \\ \end{aligned}x′=f(x)+g(x)uy=h(x)
设计 uuu 使输出 yyy 指数收敛。
yyy 的表达式中不含 uuu,将 yyy 求导得到
y′=∂h∂xx′=∂h∂x(f+gu)=∂h∂xf+∂h∂xguy'=\frac{\partial h}{\partial x}x' =\frac{\partial h}{\partial x}(f+gu) =\frac{\partial h}{\partial x}f+\frac{\partial h}{\partial x}gu y′=∂x∂hx′=∂x∂h(f+gu)=∂x∂hf+∂x∂hgu
如果 ∂h∂xg≠0\frac{\partial h}{\partial x}g\neq 0∂x∂hg=0,那么就能找到 y′y'y′ 和 uuu 的关系,取
u=1∂h∂xg(−∂h∂xf−ky)u=\frac{1}{\frac{\partial h}{\partial x}g}(-\frac{\partial h}{\partial x}f-ky)u=∂x∂hg1(−∂x∂hf−ky)
代入即可得到 y′=−kyy'=-kyy′=−ky,指数收敛。
如果 ∂h∂xg=0\frac{\partial h}{\partial x}g=0∂x∂hg=0,也就是 y′y'y′ 中不显含 uuu,那么继续求导
y′′=∂(∂h∂xf)∂xx′=∂(∂h∂xf)∂x(f+gu)=Lf2h+LgLfhuy''=\frac{\partial(\frac{\partial h}{\partial x}f)}{\partial x}x' =\frac{\partial(\frac{\partial h}{\partial x}f)}{\partial x}(f+gu) =L_f^2h + L_gL_fhu y′′=∂x∂(∂x∂hf)x′=∂x∂(∂x∂hf)(f+gu)=Lf2h+LgLfhu
其中
Lfh=∂h∂xf(x)Lf2h=∂(∂h∂xf)∂xf(x)LgLfh=∂(∂h∂xf)∂xg(x)y′=Lfh(x)+Lgh(x)u\begin{aligned} & L_fh=\frac{\partial h}{\partial x}f(x) \\ & L_f^2h=\frac{\partial(\frac{\partial h}{\partial x}f)}{\partial x}f(x) \\ & L_gL_fh=\frac{\partial(\frac{\partial h}{\partial x}f)}{\partial x}g(x) \\ & y'=L_fh(x)+L_gh(x)u \end{aligned}Lfh=∂x∂hf(x)Lf2h=∂x∂(∂x∂hf)f(x)LgLfh=∂x∂(∂x∂hf)g(x)y′=Lfh(x)+Lgh(x)u
Lg,LfL_g,L_fLg,Lf 称作李导数。继续下去,如果
LgLfρ−2h(x)=0,LgLfρ−1h(x)≠0L_gL_f^{\rho-2}h(x)=0,L_gL_f^{\rho-1}h(x)\neq 0LgLfρ−2h(x)=0,LgLfρ−1h(x)=0
则称系统具有相对阶 ρ\rhoρ,此时
y(ρ)=Lfρh(x)+LgLfρ−1h(x)uy(ρ−1)=Lfρ−1h(x)+LgLfρ−2h(x)u=Lfρ−1h(x)\begin{aligned} y^{(\rho)} =& L_f^\rho h(x)+L_gL_f^{\rho-1}h(x)u \\ y^{(\rho-1)} =& L_f^{\rho-1} h(x)+L_gL_f^{\rho-2}h(x)u=L_f^{\rho-1} h(x) \\ \end{aligned}y(ρ)=y(ρ−1)=Lfρh(x)+LgLfρ−1h(x)uLfρ−1h(x)+LgLfρ−2h(x)u=Lfρ−1h(x)
也就是对 yyy 求 ρ\rhoρ 阶导后才能显含 uuu。y=f(x)+g(x)uy=f(x)+g(x)uy=f(x)+g(x)u 的相对阶为 000。
微分同胚
输出稳定不一定能得出状态稳定,因此引入可逆变换,把系统内部的所有状态分成内部动态和输出动态两部分。前面相对阶的概念是输出动态,下面引入微分同胚的概念研究内部动态。
可逆变换 z=T(x)z=T(x)z=T(x) 中,z(t)z(t)z(t) 和 x(t)x(t)x(t) 都可导,雅可比行列式 ∂T(x)∂x\frac{\partial T(x)}{\partial x}∂x∂T(x) 不为0。(大概率?)也就是 xxx 和 T(x)T(x)T(x) 等价,可以互换,此时称 xxx 和 T(x)T(x)T(x) 是微分同胚(diffeomorphism)的。
取变换
[ξ1ξ2⋮ξρ]=[yy′⋮y(ρ−1)]\begin{bmatrix} \xi_1 \\ \xi_2 \\ \vdots \\ \xi_\rho \end{bmatrix} =\begin{bmatrix} y \\ y' \\ \vdots \\ y^{(\rho-1)} \end{bmatrix} ξ1ξ2⋮ξρ=yy′⋮y(ρ−1)
这里列出了 ρ\rhoρ 个状态,但 xxx 有 nnn 个状态,为了能让 xxx 和 zzz 微分同胚,需要对 zzz 再补充 n−ρn-\rhon−ρ 个状态,记作 η\etaη,即
z=T(x)=[ξη]z=T(x)=\begin{bmatrix} \xi \\ \hdashline \eta \end{bmatrix} z=T(x)=[ξη]
其中 η=ϕ(x)\eta=\phi(x)η=ϕ(x) 需要满足抵消条件
∂ϕ(x)∂xg(x)=0\frac{\partial\phi(x)}{\partial x}g(x)=0∂x∂ϕ(x)g(x)=0
此时
ddtϕ(x)=∂ϕ(x)∂x(f+gu)=∂ϕ(x)∂xf\frac{\text{d}}{\text{d}t}\phi(x) =\frac{\partial\phi(x)}{\partial x}(f+gu) =\frac{\partial\phi(x)}{\partial x}f dtdϕ(x)=∂x∂ϕ(x)(f+gu)=∂x∂ϕ(x)f
可以看出 ϕ(x)\phi(x)ϕ(x) 的导数与 uuu 无关,完全是内部动态。
(note: 可以类比前 ρ\rhoρ 个状态客观,后 n−ρn-\rhon−ρ 个状态不可观)
(note: 当 ρ=0,ρ=n,0<ρ
η′=f0(η,ξ)ξi′=ξi+1,1≤i≤ρ−1ξρ′=Lfρh(x)+LgLf(ρ−1)h(x)uy=ξ1\begin{aligned} & \eta'=f_0(\eta,\xi) \\ & \xi_i'=\xi_{i+1},1\le i\le\rho-1 \\ & \xi_\rho'=L_f^\rho h(x)+L_gL_f^{(\rho-1)}h(x)u \\ & y=\xi_1 \end{aligned}η′=f0(η,ξ)ξi′=ξi+1,1≤i≤ρ−1ξρ′=Lfρh(x)+LgLf(ρ−1)h(x)uy=ξ1
或
η′=f0(η,ξ)ξ′=Acξ+Bc[Lfρh(x)+LgLf(ρ−1)h(x)u]y=Ccξ\begin{aligned} & \eta'=f_0(\eta,\xi) \\ & \xi'=A_c\xi+B_c\left[L_f^\rho h(x)+L_gL_f^{(\rho-1)}h(x)u\right] \\ & y=C_c\xi \end{aligned}η′=f0(η,ξ)ξ′=Acξ+Bc[Lfρh(x)+LgLf(ρ−1)h(x)u]y=Ccξ
其中下面两式展开写作(以 ρ=3\rho=3ρ=3 为例)
ddt[ξ1ξ2ξ3]=[010001000][ξ1ξ2ξ3]+[001][Lfρh(x)+LgLf(ρ−1)h(x)u]y=[100][ξ1ξ2ξ3]\begin{aligned} & \frac{\text{d}}{\text{d}t}\begin{bmatrix} \xi_1 \\ \xi_2 \\ \xi_3 \end{bmatrix} =\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} \xi_1 \\ \xi_2 \\ \xi_3 \end{bmatrix} +\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\left[L_f^\rho h(x)+L_gL_f^{(\rho-1)}h(x)u\right] \\ & y=\begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} \xi_1 \\ \xi_2 \\ \xi_3 \end{bmatrix} \end{aligned}dtdξ1ξ2ξ3=000100010ξ1ξ2ξ3+001[Lfρh(x)+LgLf(ρ−1)h(x)u]y=[100]ξ1ξ2ξ3
能把仿射非线性系统转化成这种标准型就可以实现反馈线性化。
一个例子
下面举一个反馈线性化的例子,后面给出仿真证明推导过程无误。
[x˙1x˙2x˙3]=[−x12x1x2x2]+[2ex210]uy=2x3\begin{aligned} &\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{x}_3 \end{bmatrix} =\begin{bmatrix} -x_1 \\ 2x_1x_2 \\ x_2 \end{bmatrix} +\begin{bmatrix} 2\text{e}^{x_2} \\ 1 \\ 0 \end{bmatrix}u \\ & y = 2x_3 \end{aligned}x˙1x˙2x˙3=−x12x1x2x2+2ex210uy=2x3
y′=∂h∂xf+∂h∂xgu=Lfh=[002][−x12x1x2x2]+[002][2ex210]u=2x2y′′=Lf2h+LgLfhu=[020][−x12x1x2x2]+[020][2ex210]u=4x1x2+2u\begin{aligned} y' =& \frac{\partial h}{\partial x}f+\frac{\partial h}{\partial x}gu=L_fh \\ =& \begin{bmatrix} 0 & 0 & 2 \end{bmatrix} \begin{bmatrix} -x_1 \\ 2x_1x_2 \\ x_2 \end{bmatrix} +\begin{bmatrix} 0 & 0 & 2 \end{bmatrix} \begin{bmatrix} 2\text{e}^{x_2} \\ 1 \\ 0 \end{bmatrix}u \\ =& 2x_2 \\ y'' =& L_f^2h+L_gL_fhu \\ =& \begin{bmatrix} 0 & 2 & 0 \end{bmatrix} \begin{bmatrix} -x_1 \\ 2x_1x_2 \\ x_2 \end{bmatrix} +\begin{bmatrix} 0 & 2 & 0 \end{bmatrix} \begin{bmatrix} 2\text{e}^{x_2} \\ 1 \\ 0 \end{bmatrix}u \\ =& 4x_1x_2 + 2u \\ \end{aligned}y′===y′′===∂x∂hf+∂x∂hgu=Lfh[002]−x12x1x2x2+[002]2ex210u2x2Lf2h+LgLfhu[020]−x12x1x2x2+[020]2ex210u4x1x2+2u
可以看出系统相对阶为2。取 u=−2x1x2−4y′−4yu=-2x_1x_2-4y'-4yu=−2x1x2−4y′−4y,则 y′′=−4y′−4y,y(t)=(C1+C2t)e−2ty''=-4y'-4y,y(t)=(C_1+C_2t)\text{e}^{-2t}y′′=−4y′−4y,y(t)=(C1+C2t)e−2t,输出稳定。
下面设计变换查看系统内部是否稳定。定义变换
T(x)=[ξ1ξ2η]=[2x32x2ϕ(x)]\begin{aligned} T(x)=\begin{bmatrix} \xi_1 \\ \xi_2 \\ \eta \end{bmatrix} =\begin{bmatrix} 2x_3 \\ 2x_2 \\ \phi(x) \end{bmatrix} \end{aligned}T(x)=ξ1ξ2η=2x32x2ϕ(x)
其中 ϕ(x)\phi(x)ϕ(x) 需要满足抵消条件
∂ϕ(x)∂xg(x)=0∂ϕ∂x12ex2+∂ϕ∂x2=0\frac{\partial\phi(x)}{\partial x}g(x)=0 \\ \frac{\partial\phi}{\partial x_1}2\text{e}^{x_2} +\frac{\partial\phi}{\partial x_2}=0 ∂x∂ϕ(x)g(x)=0∂x1∂ϕ2ex2+∂x2∂ϕ=0
ϕ(x)\phi(x)ϕ(x) 的一个解为
ϕ(x)=x1−2ex2\phi(x)=x_1-2\text{e}^{x_2}ϕ(x)=x1−2ex2
得到可逆变换 z=T(x)z=T(x)z=T(x) 为
z1=ξ1=2x3z2=ξ2=2x2z3=η=x1−2ex2\begin{aligned} & z_1 = \xi_1 = 2x_3 \\ & z_2 = \xi_2 = 2x_2 \\ & z_3 = \eta = x_1-2\text{e}^{x_2} \\ \end{aligned}z1=ξ1=2x3z2=ξ2=2x2z3=η=x1−2ex2
可见雅可比矩阵 ∂T(x)∂x\frac{\partial T(x)}{\partial x}∂x∂T(x) 非奇异。此时需要注意的是如果取 ϕ(x)=x3\phi(x)=x_3ϕ(x)=x3 也能满足 (∂ϕ/∂x)g=0(\partial\phi/\partial x)g=0(∂ϕ/∂x)g=0 的条件,但此时 ϕ(x)\phi(x)ϕ(x) 中不包含 x1x_1x1 项导致雅可比矩阵的第一列全为0,不满足微分同胚的条件。
继续化成标准型,
η′=x1′−2ex2x2′=(−x1+2ex2u)−2ex2(2x1x2+u)=−x1−4x1x2ex2\eta'=x_1'-2\text{e}^{x_2}x_2' =(-x_1+2\text{e}^{x_2}u)-2\text{e}^{x_2}(2x_1x_2+u) =-x_1-4x_1x_2\text{e}^{x_2} η′=x1′−2ex2x2′=(−x1+2ex2u)−2ex2(2x1x2+u)=−x1−4x1x2ex2
标准型中 η′=f0(η,ξ)\eta'=f_0(\eta,\xi)η′=f0(η,ξ),所以接下来要把等号右边的 x1,x2x_1,x_2x1,x2 换成 η,ξ\eta,\xiη,ξ。将 x2=0.5ξ2,η=x1−2ex2x_2=0.5\xi_2,\eta = x_1-2\text{e}^{x_2}x2=0.5ξ2,η=x1−2ex2 代入得
η=x1−2e0.5ξ2,x1=η+2e0.5ξ2η′=−(η+2e0.5ξ2)−4(η+2e0.5ξ2)0.5ξ2e0.5ξ=−η−4ξ2eξ2−2ηξ2e0.5ξ2=f0(η,ξ)\begin{aligned} \eta =& x_1-2\text{e}^{0.5\xi_2},x_1=\eta+2\text{e}^{0.5\xi_2} \\ \eta' =& -(\eta+2\text{e}^{0.5\xi_2}) -4(\eta+2\text{e}^{0.5\xi_2})0.5\xi_2\text{e}^{0.5\xi} \\ =& -\eta-4\xi_2\text{e}^{\xi_2}-2\eta\xi_2\text{e}^{0.5\xi_2} =f_0(\eta,\xi) \\ \end{aligned}η=η′==x1−2e0.5ξ2,x1=η+2e0.5ξ2−(η+2e0.5ξ2)−4(η+2e0.5ξ2)0.5ξ2e0.5ξ−η−4ξ2eξ2−2ηξ2e0.5ξ2=f0(η,ξ)
这样就可以写成完整的标准型形式
η=−η−4ξ2eξ2−2ηξ2e0.5ξ2[ξ1′ξ2′]=[0100][ξ1ξ2]+[01](4x1x2+2u)y=[10]ξ1\begin{aligned} \eta =& -\eta-4\xi_2\text{e}^{\xi_2}-2\eta\xi_2\text{e}^{0.5\xi_2} \\ \begin{bmatrix} \xi_1' \\ \xi_2' \end{bmatrix} =& \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} \xi_1 \\ \xi_2 \end{bmatrix} +\begin{bmatrix} 0 \\ 1 \end{bmatrix}(4x_1x_2+2u) \\ y =& \begin{bmatrix} 1 & 0 \end{bmatrix} \xi_1 \end{aligned}η=[ξ1′ξ2′]=y=−η−4ξ2eξ2−2ηξ2e0.5ξ2[0010][ξ1ξ2]+[01](4x1x2+2u)[10]ξ1
最小相位系统
η′=f0(η,ξ)\eta'=f_0(\eta,\xi)η′=f0(η,ξ) 中,当 ξ=0\xi=0ξ=0 时系统是否渐进稳定,如果是就是最小相位系统。例子中,f0(η,0)=−ηf_0(\eta,0)=-\etaf0(η,0)=−η,是最小相位系统。
仿真
系统输入设计为
u=−2x1x2−4y′−4y=−2x1x2−8x2−8x3\begin{aligned} u =& -2x_1x_2-4y'-4y \\ =& -2x_1x_2-8x_2-8x_3 \end{aligned}u==−2x1x2−4y′−4y−2x1x2−8x2−8x3
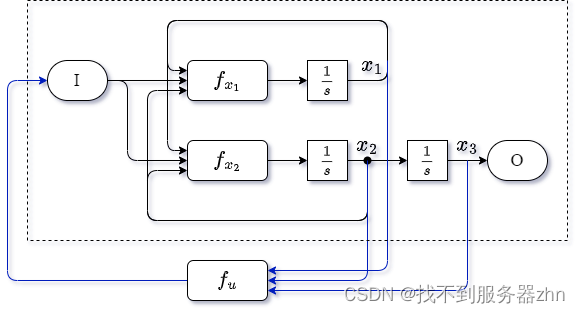
系统结构框图如图所示。
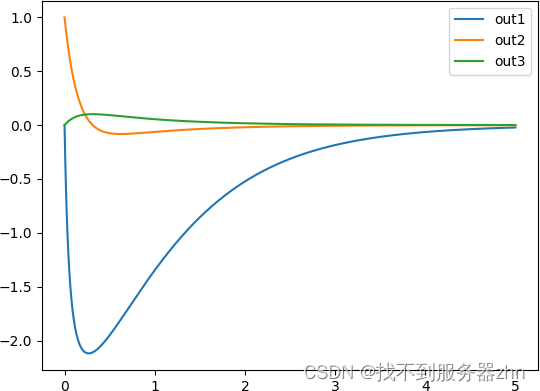
设置 x2(0)=1,x1(0)=x3(0)=0x_2(0)=1,x_1(0)=x_3(0)=0x2(0)=1,x1(0)=x3(0)=0,仿真结果如图所示。