专栏：神经网络复现目录

注意力机制

注意力机制（Attention Mechanism）是一种人工智能技术，它可以让神经网络在处理序列数据时，专注于关键信息的部分，同时忽略不重要的部分。在自然语言处理、计算机视觉、语音识别等领域，注意力机制已经得到了广泛的应用。

注意力机制的主要思想是，在对序列数据进行处理时，通过给不同位置的输入信号分配不同的权重，使得模型更加关注重要的输入。例如，在处理一句话时，注意力机制可以根据每个单词的重要性来调整模型对每个单词的注意力。这种技术可以提高模型的性能，尤其是在处理长序列数据时。

在深度学习模型中，注意力机制通常是通过添加额外的网络层实现的，这些层可以学习到如何计算权重，并将这些权重应用于输入信号。常见的注意力机制包括自注意力机制（self-attention）、多头注意力机制（multi-head attention）等。

总之，注意力机制是一种非常有用的技术，它可以帮助神经网络更好地处理序列数据，提高模型的性能。

文章目录

• 注意力机制
• 评分函数
• • 定义
  • 数学逻辑
  • 掩蔽softmax操作
  • 加性注意力
  • 缩放点积注意力

评分函数

定义

在上一节中，我们使用了高斯核的注意力汇聚函数：
f(x)=∑i=1nα(x,xi)yi=∑i=1nexp(−12(x−xi)w)2∑j=1nexp(−12(x−xi)w)2yi=∑i=1nsoftmax(−12((x−xi)w)2)yif(x)=\sum_{i=1}^n α(x,x_i)y_i \\ = \sum_{i=1}^n{\frac{exp(-\frac{1}{2}(x - x_i)w)^2} {\sum_{j=1}^n exp(-\frac{1}{2}(x - x_i)w)^2}}y_i \\ =\sum_{i=1}^nsoftmax(-\frac{1}{2}((x-x_i)w)^2)y_if(x)=i=1∑n​α(x,xi​)yi​=i=1∑n​∑j=1n​exp(−21​(x−xi​)w)2exp(−21​(x−xi​)w)2​yi​=i=1∑n​softmax(−21​((x−xi​)w)2)yi​

其中高斯核的指数部分即为评分函数，衡量一个输入序列中每个元素与当前输出元素之间的相似度得分，用于计算权重。

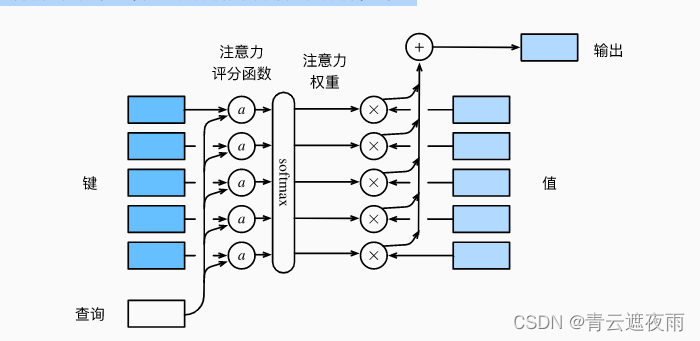
从宏观来看，上述算法可以用来实现图中的注意力机制框架。 图10.3.1说明了 如何将注意力汇聚的输出计算成为值的加权和， 其中α\alphaα表示注意力评分函数。 由于注意力权重是概率分布， 因此加权和其本质上是加权平均值。

数学逻辑

假设有一个查询qqq和m个键值对(k1,v1),....,(km,vm)(k_1,v_1),....,(k_m,v_m)(k1​,v1​),....,(km​,vm​)。注意力汇聚函数fff就被表示成值的加权和：
f(q,(k1,v1),....,(km,vm))=∑n=1mα(q,ki)vif(q,(k_1,v_1),....,(k_m,v_m))=\sum_{n=1}^m \alpha(q,k_i)v_if(q,(k1​,v1​),....,(km​,vm​))=n=1∑m​α(q,ki​)vi​
其中查询qqq和键kik_iki​的注意力权重（标量） 是通过注意力评分函数α\alphaα将两个向量映射成标量， 再经过softmax运算得到的：
α(q,ki)=softmax(a(q,ki))=exp(a(q,ki))∑j=1mexp(q,ki)\alpha(q,k_i)=softmax(a(q,k_i))=\frac{exp(a(q,k_i))}{\sum_{j=1}^m exp(q,k_i)}α(q,ki​)=softmax(a(q,ki​))=∑j=1m​exp(q,ki​)exp(a(q,ki​))​

正如上图所示，选择不同的注意力评分函数α\alphaα会导致不同的注意力汇聚操作。 本节将介绍两个流行的评分函数，稍后将用他们来实现更复杂的注意力机制。

掩蔽softmax操作

正如上面提到的，softmax操作用于输出一个概率分布作为注意力权重。 在某些情况下，并非所有的值都应该被纳入到注意力汇聚中。 例如，为了高效处理小批量数据集， 某些文本序列被填充了没有意义的特殊词元。 为了仅将有意义的词元作为值来获取注意力汇聚， 可以指定一个有效序列长度（即词元的个数）， 以便在计算softmax时过滤掉超出指定范围的位置。 下面的masked_softmax函数 实现了这样的掩蔽softmax操作（masked softmax operation）， 其中任何超出有效长度的位置都被掩蔽并置为0。

def sequence_mask(X, valid_len, value=0):maxlen = X.size(1)mask = torch.arange((maxlen), dtype=torch.float32,device=X.device)[None, :] < valid_len[:, None]X[~mask] = valuereturn X

#@save
def masked_softmax(X, valid_lens):"""通过在最后一个轴上掩蔽元素来执行softmax操作"""# X:3D张量，valid_lens:1D或2D张量if valid_lens is None:return nn.functional.softmax(X, dim=-1)else:shape = X.shapeif valid_lens.dim() == 1:valid_lens = torch.repeat_interleave(valid_lens, shape[1])else:valid_lens = valid_lens.reshape(-1)# 最后一轴上被掩蔽的元素使用一个非常大的负值替换，从而其softmax输出为0X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens,value=-1e6)return nn.functional.softmax(X.reshape(shape), dim=-1)

这个函数实现了一个 softmax 操作，并通过掩蔽一些元素来处理序列中的变长情况。下面是每个参数的解释：

X：一个三维张量，形状为（batch_size，seq_len，feat_size）。
valid_lens：一个一维或二维张量，指示每个序列的有效长度。如果是一维张量，则意味着每个序列的有效长度都相同；如果是二维张量，则意味着每个序列的有效长度不同。
如果 valid_lens 为 None，则函数将使用普通的 softmax 函数对 X 进行操作，而不考虑序列的有效长度。否则，函数将在最后一个轴上掩蔽一些元素，以使它们的 softmax 输出为 0。

为了实现这个掩蔽操作，函数首先检查 valid_lens 是否是一个一维张量。如果是，它会将 valid_lens 重复 shape[1] 次，这样每个序列的有效长度都可以用一个相同的长度来表示。如果 valid_lens 是一个二维张量，则将其重塑为一个一维张量。然后，函数使用 d2l.sequence_mask 函数将要掩蔽的元素替换为一个非常大的负值（-1e6），这样 softmax 的输出就会变成 0。

最后，函数重新将 X 重塑为其原始形状，并在最后一个轴上使用 nn.functional.softmax 函数计算 softmax。

为了演示此函数是如何工作的， 考虑由两个2×\times× 4矩阵表示的样本， 这两个样本的有效长度分别为2和3。 经过掩蔽softmax操作，超出有效长度的值都被掩蔽为0。

masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))

加性注意力

一般来说，当查询和键是不同长度的矢量时，可以使用加性注意力作为评分函数。 给定查询
和qqq键kik_iki​， 加性注意力（additive attention）的评分函数为:
a(q,k)=wv⊺tanh(Wqq+Wkk）a(q,k)=w_v^\intercal tanh(W_q q+W_k k）a(q,k)=wv⊺​tanh(Wq​q+Wk​k）
中可学习的参数是WqW_qWq​、WkW_kWk​ 和wvw_vwv​ 。将查询和键连结起来后输入到一个多层感知机（MLP）中， 感知机包含一个隐藏层，其隐藏单元数是一个超参数h。 通过使用tanhtanhtanh作为激活函数，并且禁用偏置项。

下面来实现加性注意力。

#@save
class AdditiveAttention(nn.Module):"""加性注意力"""def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):super(AdditiveAttention, self).__init__(**kwargs)self.W_k = nn.Linear(key_size, num_hiddens, bias=False)self.W_q = nn.Linear(query_size, num_hiddens, bias=False)self.w_v = nn.Linear(num_hiddens, 1, bias=False)self.dropout = nn.Dropout(dropout)def forward(self, queries, keys, values, valid_lens):queries, keys = self.W_q(queries), self.W_k(keys)# 在维度扩展后，# queries的形状：(batch_size，查询的个数，1，num_hidden)# key的形状：(batch_size，1，“键－值”对的个数，num_hiddens)# 使用广播方式进行求和features = queries.unsqueeze(2) + keys.unsqueeze(1)features = torch.tanh(features)# self.w_v仅有一个输出，因此从形状中移除最后那个维度。# scores的形状：(batch_size，查询的个数，“键-值”对的个数)scores = self.w_v(features).squeeze(-1)self.attention_weights = masked_softmax(scores, valid_lens)# values的形状：(batch_size，“键－值”对的个数，值的维度)return torch.bmm(self.dropout(self.attention_weights), values)

这段代码定义了一个名为AdditiveAttention的类，它实现了加性注意力机制。__init__函数接受四个参数：key_size，query_size，num_hiddens和dropout。

forward函数接受四个参数：queries，keys，values和valid_lens。其中，queries是一个形状为(batch_size, query_size)的张量，keys是一个形状为(batch_size, num_items, key_size)的张量，values是一个形状为(batch_size, num_items, value_size)的张量，valid_lens是一个形状为(batch_size,)的张量，其中包含每个示例中键-值对的有效长度。

在forward函数中，使用线性层将keys和queries转换为大小为num_hiddens的张量。然后使用unsqueeze(2)将queries张量扩展为(batch_size, num_queries, 1, num_hiddens)，使用unsqueeze(1)将keys张量扩展为(batch_size, 1, num_items, num_hiddens)。这些张量被加在一起，创建一个形状为(batch_size, num_queries, num_items, num_hiddens)的张量。对该张量应用tanh激活函数，得到一个形状相同的张量。

接下来，将张量传递到具有单个输出的线性层(self.w_v)中，得到一个形状为(batch_size, num_queries, num_items, 1)的张量。通过压缩最后一个维度来删除单例维度，得到一个形状为(batch_size, num_queries, num_items)的张量。

最后，使用masked_softmax函数计算注意力权重，该函数将softmax函数应用于得分张量沿着num_items维度，同时忽略每个示例之外的元素。使用注意力权重计算values张量的加权和，使用torch.bmm函数，得到一个形状为(batch_size, num_queries, value_size)的张量。

在计算加权和之前，应用dropout函数于注意力权重，并将注意力权重存储在self.attention_weights变量中，以便于调试或可视化。

下面是理解重点：

在这个代码段中， features = queries.unsqueeze(2) + keys.unsqueeze(1)是实现加性注意力的关键步骤之一。 在这里，我们将查询张量 queries 和键张量 keys 进行扩展，并在中间维度进行广播加法。 这样就创建了一个新的张量 features，其中 features[i][j][k] 表示查询张量中第 i 个查询向量和键张量中第 k 个键向量之间的相似度加上一个偏置后的结果，作为注意力机制中的相似度分数。

具体来说，queries.unsqueeze(2)将 queries 张量中的维度2扩展，也就是在中间增加了一个维度。这样，queries 的形状变成 (batch_size, 查询的个数, 1, num_hidden)。类似地，keys.unsqueeze(1)将 keys 张量中的维度1扩展，也就是在第一个维度上增加了一个维度，这样 keys 的形状变成 (batch_size, 1, 键-值对的个数, num_hidden)。

接下来，这两个张量 queries 和 keys 就可以使用广播的方式相加，也就是在维度2和1上广播。这样，得到的 features 张量的形状就是 (batch_size, 查询的个数, 键-值对的个数, num_hidden)。

最后，我们使用tanh函数对 features 进行激活，得到的张量形状不变。这一步通常被称为非线性变换或者映射。

用一个小例子来演示上面的AdditiveAttention类， 其中查询、键和值的形状为（批量大小，步数或词元序列长度，特征大小）， 实际输出为(2,1,20)、(2,10,2)和(2,10,4)。 注意力汇聚输出的形状为（批量大小，查询的步数，值的维度）。

queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
# values的小批量，两个值矩阵是相同的
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(2, 1, 1)
valid_lens = torch.tensor([2, 6])attention = AdditiveAttention(key_size=2, query_size=20, num_hiddens=8,dropout=0.1)
attention.eval()
attention(queries, keys, values, valid_lens)

缩放点积注意力

使用点积可以得到计算效率更高的评分函数， 但是点积操作要求查询和键具有相同的长度ddd。 假设查询和键的所有元素都是独立的随机变量， 并且都满足零均值和单位方差， 那么两个向量的点积的均值为000，方差为ddd。 为确保无论向量长度如何， 点积的方差在不考虑向量长度的情况下仍然是1， 我们再将点积除以d\sqrt{d}d​， 则缩放点积注意力（scaled dot-product attention）评分函数为：

a(q,k)=q⊺k/da(q,k)=q^\intercal k/\sqrt{d}a(q,k)=q⊺k/d​

在实践中，我们通常从小批量的角度来考虑提高效率， 例如基于n个查询和m个键－值对计算注意力， 其中查询和键的长度为d，值的长度为v。 查询Q∈\in∈Rn×dR^{n\times d}Rn×d、 键K∈\in∈Rm×dR^{m\times d}Rm×d和值V∈\in∈Rm×vR^{m\times v}Rm×v的缩放点积注意力是：
softmax(QK⊺d)Vsoftmax(\frac{QK^{\intercal}}{\sqrt{d}})Vsoftmax(d​QK⊺​)V
下面的缩放点积注意力的实现使用了暂退法进行模型正则化。

#@save
class DotProductAttention(nn.Module):"""缩放点积注意力"""def __init__(self, dropout, **kwargs):super(DotProductAttention, self).__init__(**kwargs)self.dropout = nn.Dropout(dropout)# queries的形状：(batch_size，查询的个数，d)# keys的形状：(batch_size，“键－值”对的个数，d)# values的形状：(batch_size，“键－值”对的个数，值的维度)# valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)def forward(self, queries, keys, values, valid_lens=None):d = queries.shape[-1]# 设置transpose_b=True为了交换keys的最后两个维度scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)self.attention_weights = masked_softmax(scores, valid_lens)return torch.bmm(self.dropout(self.attention_weights), values)

为了演示上述的DotProductAttention类， 我们使用与先前加性注意力例子中相同的键、值和有效长度。 对于点积操作，我们令查询的特征维度与键的特征维度大小相同。

queries = torch.normal(0, 1, (2, 1, 2))
attention = DotProductAttention(dropout=0.5)
attention.eval()
attention(queries, keys, values, valid_lens)