LeetCode 123 买卖股票的最佳时机III

题目链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/

思路：

二维数组

• dp数组的含义

总共有五种操作：

• 不操作

• 第一次持有该股票

• 第一次不持有该股票

• 第二次持有该股票

• 第二次不持有该股票

dp[i][1]代表在第i天第一次持有该股票时的最大现金

dp[i][2]代表在第i天第一次不持有该股票时的最大现金

dp[i][3]代表在第i天第二次持有该股票时的最大现金

dp[i][4]代表在第i天第二次不持有该股票时的最大现金

• 递推公式

因为本题是最多二次买卖，所以有不发生买卖，仅买卖一次，买卖两次的三种情况

第i天第一次持有该股票有两种情况：1、第i-1天时就持有了。2、在第i天时第一次买入股票

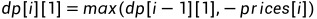
第i天第一次不持有该股票有两种情况：1、第i-1天时就不持有了。2、在第i天时第一次卖出股票

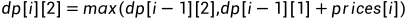
同理可推出后续的递推公式：

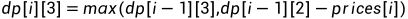
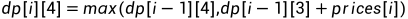
• 初始化

第0天没有操作，这个最容易想到，就是0，即：dp[0][0] = 0;

第0天做第一次买入的操作，dp[0][1] = -prices[0];

第0天做第一次卖出的操作，这个初始值应该是多少呢？

此时还没有买入，怎么就卖出呢？ 其实可以理解当天买入，当天卖出，所以dp[0][2] = 0;

第0天第二次买入操作，初始值应该是多少呢？

第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。

所以第二次买入操作，初始化为：dp[0][3] = -prices[0];

同理第二次卖出初始化dp[0][4] = 0;

• 遍历顺序

由递推公式可知，第i天时的最大金额和第i-1天的状态有关，所以必然是从前往后遍历。

三维数组

• dp数组的含义

dp[1][i][0]代表在第i天第一次持有该股票时的最大现金

dp[1][i][1]代表在第i天第一次不持有该股票时的最大现金

dp[2][i][0]代表在第i天第二次持有该股票时的最大现金

dp[2][i][1]代表在第i天第二次不持有该股票时的最大现金

• 递推公式

因为本题是最多二次买卖，所以有不发生买卖，仅买卖一次，买卖两次的三种情况

第i天第一次持有该股票有两种情况：1、第i-1天时就持有了。2、在第i天时第一次买入股票

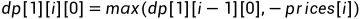
第i天第一次不持有该股票有两种情况：1、第i-1天时就不持有了。2、在第i天时第一次卖出股票

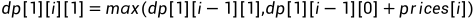
同理可推出后续的递推公式：

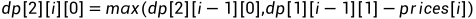
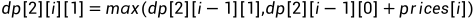
• 初始化

第0天没有操作，这个最容易想到，就是0，即：dp[0][0][0] = 0;

第0天做第一次买入的操作，dp[1][0][0] = -prices[0];

第0天做第一次卖出的操作，这个初始值应该是多少呢？

此时还没有买入，怎么就卖出呢？ 其实可以理解当天买入，当天卖出，所以dp[1][0][1] = 0;

第0天第二次买入操作，初始值应该是多少呢？

第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。

所以第二次买入操作，初始化为：dp[2][0][0] = -prices[0];

同理第二次卖出初始化dp[2][0][1] = 0;

• 遍历顺序

由递推公式可知，第i天时的最大金额和第i-1天的状态有关，所以必然是从前往后遍历。

代码：

• 二维数组

class Solution {
public:int maxProfit(vector& prices) {vector>dp(prices.size(), vector(5, 0));dp[0][1] = -prices[0];dp[0][3] = -prices[0];for(int i = 1; i < prices.size(); i++){dp[i][1] = max(dp[i - 1][1], -prices[i]);dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);}return max(dp[prices.size() - 1][2], dp[prices.size() - 1][4]);}
};

• 三维数组

class Solution {
public:int maxProfit(vector& prices) {if(prices.size() == 1)  return 0;vector>>dp(3, vector>(prices.size(), vector(2, 0)));dp[1][0][0] = -prices[0];dp[2][0][0] = -prices[0];for(int i = 1; i < prices.size(); i++){dp[1][i][0] = max(dp[1][i - 1][0], -prices[i]);dp[1][i][1] = max(dp[1][i - 1][1], dp[1][i - 1][0] + prices[i]);dp[2][i][0] = max(dp[2][i - 1][0], dp[1][i - 1][1] - prices[i]);dp[2][i][1] = max(dp[2][i - 1][1], dp[2][i - 1][0] + prices[i]);}return max(dp[1][prices.size() - 1][1], dp[2][prices.size() - 1][1]);}
};

总结

在第0天第二次买入的初始化中初始化错误，写出了三维数组的代码。

LeetCode 188 买卖股票的最佳时机IV

题目链接：https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/

思路：

本题是123.买卖股票的最佳时机III的进阶版，最多有k次交易。

• dp数组的含义

总共有2*k+1种操作：

• 不操作

• 第一次持有该股票

• 第一次不持有该股票

• 第二次持有该股票

• 第二次不持有该股票

• ...

dp[i][1]代表在第i天第一次持有该股票时的最大现金

dp[i][2]代表在第i天第一次不持有该股票时的最大现金

dp[i][3]代表在第i天第二次持有该股票时的最大现金

dp[i][4]代表在第i天第二次不持有该股票时的最大现金

...

• 递推公式

因为本题是最多k次买卖，

第i天第一次持有该股票有两种情况：1、第i-1天时就持有了。2、在第i天时第一次买入股票

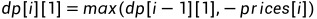
第i天第一次不持有该股票有两种情况：1、第i-1天时就不持有了。2、在第i天时第一次卖出股票

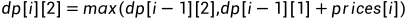
后续的递推公式：

...

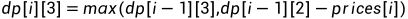
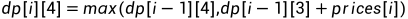
可以发现奇数是买入，偶数是卖出（除0外）

所以整体的递推公式为：

for (int j = 0; j < 2 * k - 1; j += 2) {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}

• 初始化

第0天没有操作，这个最容易想到，就是0，即：dp[0][0] = 0;

第0天做第一次买入的操作，dp[0][1] = -prices[0];

第0天做第一次卖出的操作，这个初始值应该是多少呢？

此时还没有买入，怎么就卖出呢？ 其实可以理解当天买入，当天卖出，所以dp[0][2] = 0;

第0天第二次买入操作，初始值应该是多少呢？

第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。

所以第二次买入操作，初始化为：dp[0][3] = -prices[0];

同理第二次卖出初始化dp[0][4] = 0;

所以，只要是奇数都是-prices[0]

for(int i = 1; i < num; i += 2)
{dp[0][i] = -prices[0]; }

• 遍历顺序

由递推公式可知，第i天时的最大金额和第i-1天的状态有关，所以必然是从前往后遍历。

代码：

class Solution {
public:int maxProfit(int k, vector& prices) {if(prices.empty() || prices.size() == 1)    return 0;int num = 1 + 2 * k;vector>dp(prices.size(), vector(num, 0));for(int i = 1; i < num; i += 2){dp[0][i] = -prices[0]; }for(int i = 1; i < prices.size(); i++){for (int j = 0; j < num - 1; j += 2) {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);}}  return dp[prices.size() - 1][num - 1];}
};

总结

是前一道题的进阶版，相对简单。

今日总结：

要注意初始化。