fwdiary(2) dp2
1.传纸条
AcWing 275. 传纸条 - AcWing
走两条路,走一条最大的再走一条次最大的显然不是合起来最大的,那么只能考虑同时走,同时走就需要记录两条路线的坐标,那么有4维。考虑走了k步,那么就另一维就可以由k推出,降为3维。
2.I区域
276. I-区域 - AcWing题库
经典维度,前i行,选了j个。分析题目特性,可能还需要第i行选择的区间l,r,因为先扩张后缩短,再加两维表示左右端是否进入缩短阶段。
记录方案:用pre表示是从哪个状态转移过来的。每次遍历到j==k时就记录一次最大值和当前状态。
#include
#include
#include
using namespace std;const int N =16;int f[N][N*N][N][N][2][2];//最后两维状态表示 当前左右端处于扩张或缩短
struct S{int i, j, l, r, x, y;
}pre[N][N * N][N][N][2][2], t;int n,m,k;
int a[N][N];
int ans;int cost(int i,int l,int r)
{return a[i][r]-a[i][l-1];
}void print(S x){if(x.j == 0) return;print(pre[x.i][x.j][x.l][x.r][x.x][x.y]);for(int i = x.l; i <= x.r; i++) printf("%d %d\n", x.i, i);
}int main()
{cin>>n>>m>>k;for(int i = 1; i <= n; i++)for(int j = 1; j <= m; j++)scanf("%d", &a[i][j]), a[i][j] += a[i][j - 1];for(int i = 1; i <= n; i++){for(int j = 1; j <= k; j++){for(int l = 1; l <= m; l++){for(int r = l; r <= m; r++){if(j < r - l + 1) continue;//x = 0, y = 0;for(int l1 = l; l1 <= r; l1++){for(int r1 = l1; r1 <= r; r1++){int &v = f[i][j][l][r][0][0], val = f[i - 1][j - (r - l + 1)][l1][r1][0][0] + cost(i, l, r);if(v < val) {v = val, pre[i][j][l][r][0][0] = (S){i - 1, j - (r - l + 1), l1, r1, 0, 0};}}}//x = 0, y = 1;for(int l1 = l; l1 <= r; l1++){for(int r1 = r; r1 <= m; r1++){for(int y1 = 0; y1 < 2; y1++) {int &v = f[i][j][l][r][0][1], val = f[i - 1][j - (r - l + 1)][l1][r1][0][y1] + cost(i, l, r);if(v < val) {v = val, pre[i][j][l][r][0][1] = (S){i - 1, j - (r - l + 1), l1, r1, 0, y1};}}}}// x = 1, y = 0;for(int l1 = 1; l1 <= l; l1++){for(int r1 = l; r1 <= r; r1++){for(int x1 = 0; x1 < 2; x1++) {int &v = f[i][j][l][r][1][0], val = f[i - 1][j - (r - l + 1)][l1][r1][x1][0] + cost(i, l, r);if(v < val) {v = val, pre[i][j][l][r][1][0] = (S){i - 1, j - (r - l + 1), l1, r1, x1, 0};} }}}// x = 1, y = 1;for(int l1 = 1; l1 <= l; l1++){for(int r1 = r; r1 <= m; r1++){for(int x1 = 0; x1 < 2; x1++) {for(int y1 = 0; y1 < 2; y1++) {int &v = f[i][j][l][r][1][1], val = f[i - 1][j - (r - l + 1)][l1][r1][x1][y1] + cost(i, l, r);if(v < val) {v = val, pre[i][j][l][r][1][1] = (S){i - 1, j - (r - l + 1), l1, r1, x1, y1};}}}}}if(j == k){for(int x = 0; x < 2; x++) {for(int y = 0; y < 2; y++) {if(ans < f[i][j][l][r][x][y]) {ans = f[i][j][l][r][x][y], t = (S){i, j, l, r, x, y};}}}}}}}}printf("Oil : %d\n",ans);print(t);return 0;} 3.饼干
277. 饼干 - AcWing题库
经典状态表示前i个人,分了j个饼干。
首先由排序不等式,贪婪度大的孩子分得的饼干一定更多。
因此f包含的集合是:前i个人,分了j个饼干,并且饼干数递减的方案。
接下来需要划分集合,如果以最后一个人分得的饼干数为划分,则不知道之前有多少人比该人分得的饼干多。因此考虑900. 整数划分 - AcWing题库
类似的划分。即有k个人分得的饼干是1。(相对的1)
状态表示:分得0个,则等于所有人减1个饼干,直到最少的饼干数是1.所以方案数可以等价于i个人分得j-i个饼干的方案数。所以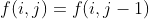 .
.
分得k个,![f[i][j]=min(f[i][j],f[i-k][j-k]+(s[i]-s[i-k])*(i-k))](/uploadfile/202506/4b62b8a13ef0.gif)
处理一个疑问:如何知道i-k的结尾不是1。答案:分得的饼干1是一个相对量,i-k处的饼干数一定大于1。
求方案,从结尾倒着求,还需要记录偏移量h。如果出现结尾0个1的情况,则h++
#include
#include
#include
using namespace std;const int N =31,M=5010;
typedef pair PII;int n,m;
PII g[N];
int s[N];
int f[N][M];
int ans[N];int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>g[i].first;g[i].second=i;}sort(g+1,g+n+1);reverse(g+1,g+n+1);for(int i=1;i<=n;i++) s[i]=s[i-1]+g[i].first;memset(f,0x3f,sizeof f);f[0][0]=0;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){if(j>=i) f[i][j]=f[i][j-i];for(int k=1;k<=i&&k<=j;k++)f[i][j]=min(f[i][j],f[i-k][j-k]+(s[i]-s[i-k])*(i-k));}cout<=i&&f[i][j]==f[i][j-i]) j-=i,h++;else{for(int k=1;k<=i&&k<=j;k++)if(f[i][j]==f[i-k][j-k]+(s[i]-s[i-k])*(i-k)){for(int u=i;u>i-k;u--)ans[g[u].second]=1+h;i-=k,j-=k;break;}}}for(int i=1;i<=n;i++) cout< 4.陪审团
280. 陪审团 - AcWing题库
要求,d+p最大,差值最小。从n个里面选m个。
其实就是背包问题的套路。因此状态表示:前i个选,选不超过j个,差值为v的d+p最大的方案。
首先给差值v加上一个偏移量使得v一定大于0
求最大值,初始化为负无穷,f[0][0][base]=0;
状态划分,选与不选。如果选了![f[i][j][k] = max(f[i][j][k], f[i - 1][j - 1][t] + p[i] + d[i]);](/uploadfile/202506/08f5f4f0d535.gif)
求目标方案:base+v,base-v开始搜,如果搜到其中一个不为0,则证明找到答案,取此时base+v,base-v中d+p最大的状态。
接着从末尾开始搜具体方案。
#include
#include
#include
using namespace std;const int N =210,M=810,base=400;
//转变为01背包问题,求前i个人选j个 差值是m的最大总分方案int f[N][21][M];
int p[N],d[N];
int ans[N];
int n,m;int main()
{int T=1;while(scanf("%d%d", &n, &m), n || m){for(int i=1;i<=n;i++) cin>>p[i]>>d[i];memset(f,-0x3f,sizeof f);f[0][0][base]=0;for (int i = 1; i <= n; i ++ )for (int j = 0; j <= m; j ++ )for (int k = 0; k < M; k ++ ){f[i][j][k] = f[i - 1][j][k];int t = k - (p[i] - d[i]);if (t < 0 || t >= M) continue;if (j < 1) continue;f[i][j][k] = max(f[i][j][k], f[i - 1][j - 1][t] + p[i] + d[i]);}int v=0;while(f[n][m][base-v]<0&&f[n][m][base+v]<0) v++;if(f[n][m][base-v]>f[n][m][base+v]) v=base-v;else v=base+v;int cnt=0;int i=n,j=m,k=v;while(j){if(f[i][j][k]==f[i-1][j][k]) i--;else{ans[cnt++]=i; k-=(p[i]-d[i]);j--;i--;}}int sp = 0, sd = 0;for (int i = 0; i < cnt; i ++ ){sp += p[ans[i]];sd += d[ans[i]];}printf("Jury #%d\n", T ++ );printf("Best jury has value %d for prosecution and value %d for defence:\n", sp, sd);sort(ans, ans + cnt);for (int i = 0; i < cnt; i ++ ) printf(" %d", ans[i]);puts("\n");}
} 树形dp
5.多边形
283. 多边形 - AcWing题库
显然是个区间dp了,再发现是个环形,所以倍增一下。
求最大值,注意有个乘号运算,因此最大值不一定有两个区间的最大值运算得来,因此状态还需要记录最小值。
所以状态表示:区间i到j,多加一维状态0 1 表示最大值和最小值。
状态转移:

#include
#include
#include using namespace std;const int N = 55, INF = 0x3f3f3f3f;
int q[N*2], f[N*2][N*2][2];
char op[N*2];int n;int get(int a, int b, char ch){if(ch == 'x') return a * b;else return a + b;
}int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>op[i]>>q[i];op[i+n]=op[i];q[i+n]=q[i];}for(int i=1;i<=2*n;i++)for(int j=i;j<=2*n;j++)if(i==j) f[i][j][0]=f[i][j][1]=q[i];else f[i][j][0]=-INF,f[i][j][1]=INF;for(int len=2;len<=n;len++)for(int i=1;i+len-1<=2*n;i++){int l=i,r=i+len-1;for(int k=l;k 6.选课
题意:选某门课必须选先修课。每门课有个学分,目标是选m门课的方案中学分最多的。
没有先修课,则父节点为0,因此0是根节点,最终答案要把0选上,所以实际上是m+1个结点。
状态表示应该是以u为根的子树,选择j门课,学分最多的方案。
状态转移:遍历所有子树,注意遍历时最多只能选择m-1门课,因为第m门课要选根节点。每个子树里面实际上有以子树为根,选择1~m门课的方案。因此是个01背包问题。emm实际上整体看起来又有点像分组背包问题。
最后再选择根节点。
#include
#include
#include
using namespace std;const int N =310;int f[N][N];
int n,m;
int w[N];int h[N],e[N],ne[N],idx;void add(int a,int b)
{e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}void dfs(int u)
{for(int i=h[u];~i;i=ne[i]){int j=e[i];dfs(j);for(int k=m-1;k>=0;k--)for(int s=1;s<=k;s++)f[u][k]=max(f[u][k],f[u][k-s]+f[j][s]);}for(int i=m;i;i--) f[u][i]=f[u][i-1]+w[u];f[u][0]=0;return ;
}int main()
{cin>>n>>m;memset(h,-1,sizeof h);for(int i=1;i<=n;i++){int fa;cin>>fa>>w[i];add(fa,i);}m++;dfs(0);cout< 状压
7.蒙德里安的梦想
只能说很经典。
状态表示一般都是覆盖前i列,在第i列的状态。
这题稍有改动,但是不难想,状态表示为覆盖前i-1列,伸出在第i列的状态j。
枚举横条摆放方案,剩下的竖条只能一种方案填入。因此答案就等价于横条摆放方案。
状态转移:第i行伸出到j,第i-1行伸出到i行k。j|k不能有奇数个连续空位。j&k必须0
#include
#include
#include
#include using namespace std;typedef long long LL;const int N = 12, M = 1 << N;int n, m;
LL f[N][M];
vector state[M];
bool st[M];int main()
{while(cin>>n>>m,n||m){for(int i=0;i<1<>j&1) {if(cnt&1){is_valid=false;break;}cnt=0;}else cnt++;}if(cnt&1) is_valid=false;st[i]=is_valid;}for(int i=0;i<1< 8.炮兵
一行的摆放会影响后面两行。一次状态表示需要记录两行数据,与前第三行的状态作为划分。
设i行为a,i-1行为b,i-2行为c。本题求摆放个数,因此多加一维状态记录摆放数
a&b a&c b&c 都为0。 每一行也有约束
地图给状态的限制。这个数据处理方法要记一下。
状压dp的经典处理:先遍历,求出满足单行约数的状态。求出状态i能转移去的状态,或者能转移到状态i的状态。 循环时遍历对应状态即可。不过这道题没用到,,
#include
#include
#include
#include
using namespace std;const int N =110,M=1<<11;
int f[2][M][M];//摆放前i列,第i行状态b,第i-1行a, 用第i-2行c划分
int n,m;
int cnt[M];
vector state;
int g[N];int count(int state)
{int res=0;for(int i=0;i>i&1;return res;
}bool check(int state)//检测单论一行的状态合不合法
{for(int i=0;i>i&1)&&((state>>i+1&1)|(state>>i+2&1))) return false;return true;
}int main()
{cin>>n>>m;for(int i=1;i<=n;i++)for(int j=0;j>c;if(c=='H') g[i]+=1< 唉 鼠鼠还是做不出困难题,中等题看运气。哭了
上一篇:常用的DOS命令
下一篇:无刷直流电机介绍及单片机控制实例