【题目描述】

七段码 HUSTOJ 题目导出文件

[蓝桥杯2020] 第十一届蓝桥杯第二次省赛—填空题E题

七段码

小蓝要用七段码数码管来表示一种特殊的文字。

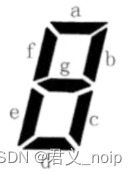
上图给出了七段码数码管的一个图示，数码管中一共有 7 段可以发光的二
极管，分别标记为 a, b, c, d, e, f, g。
小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符的表达时，要求所有发光的二极管是连成一片的。
例如：b 发光，其他二极管不发光可以用来表达一种字符。
例如：c 发光，其他二极管不发光可以用来表达一种字符。这种方案与上一行的方案可以用来表示不同的字符，尽管看上去比较相似。
例如：a, b, c, d, e 发光，f, g 不发光可以用来表达一种字符。
例如：b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光的二极管没有连成一片。请问，小蓝可以用七段码数码管表达多少种不同的字符？

【题目考点】

1. 深搜（子集树）

2. 图论 连通图（并查集，深搜）

【解题思路】

七段数码管中每个管是一个顶点，相邻的管之间有一条边，建立无向图：

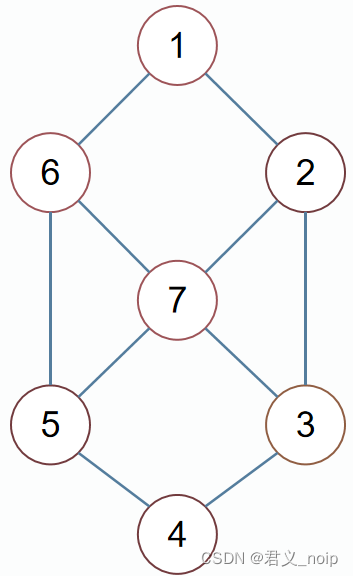
一些数码管亮，相当于在图中选择一些顶点，让这些顶点对应的数码管亮起，其它数码管不亮。要求选择的数码管连成一片，也就是选择的顶点和选择顶点之间的边构成的子图必须是连通图。
选择的顶点是所有顶点的子集，通过深搜子集树遍历每种可能的选择顶点的方案。
对于每种选择顶点的方案，判断选择的顶点，及选择顶点之间的边构成的子图是不是连通图。
判断一个图是否是连通图，可以使用并查集，也可以使用深搜的方法。

【题解代码】

答案：80

解法1：邻接矩阵 并查集判断连通图

#include
using namespace std;
#define N 10
int fa[N], ans;
int edge[N][N];
bool sel[N];//sel[i]：管i亮了 
void init(int n)
{for(int i = 1; i <= n; ++i)fa[i] = i;
}
int find(int x)
{if(fa[x] == x)return x;elsereturn fa[x] = find(fa[x]);
}
void merge(int x, int y)
{fa[find(x)] = find(y);
}
void addEdge(int u, int v)
{edge[u][v] = edge[v][u] = 1;
}
void initGraph()
{addEdge(1, 2);addEdge(2, 3);addEdge(3, 4);addEdge(4, 5);addEdge(5, 6);addEdge(6, 1);addEdge(6, 7);addEdge(5, 7);addEdge(2, 7);addEdge(3, 7);
}
bool check()//判断是否是连通图 
{init(7);int ct = 0;for(int i = 1; i <= 7; ++i)for(int j = 1; j <= 7; ++j)if(edge[i][j] && sel[i] && sel[j])merge(i, j);for(int i = 1; i <= 7; ++i)if(fa[i] == i && sel[i])//管i亮着且是根结点 ct++;return ct == 1;
}
void dfs(int k)//管k是否亮
{if(k > 7){if(check())ans++;return;}dfs(k+1);sel[k] = true;dfs(k+1);sel[k] = false; 
} 
int main()
{init(7);initGraph();dfs(1);cout << ans;return 0;
} 

解法2：邻接表 深搜判断连通图

#include
using namespace std;
#define N 10
int ans;
vector edge[N];
bool vis[N], sel[N];//sel[i]：管i亮了 
void addEdge(int u, int v)
{edge[u].push_back(v);edge[v].push_back(u);
}
void initGraph()
{addEdge(1, 2);addEdge(2, 3);addEdge(3, 4);addEdge(4, 5);addEdge(5, 6);addEdge(6, 1);addEdge(6, 7);addEdge(5, 7);addEdge(2, 7);addEdge(3, 7);
}
void dfsGraph(int u)//对图做深搜
{for(int v : edge[u]){if(sel[v] && vis[v] == false)//注意只能访问已选择的顶点{vis[v] = true;dfsGraph(v);}}
}
bool check()//判断是否是连通图 
{memset(vis, 0, sizeof(vis));int ct = 0;//连通分量个数 for(int v = 1; v <= 7; ++v){if(sel[v] && vis[v] == false){ct++;//连通分量个数增加1 vis[v] = true;dfsGraph(v);}}return ct == 1;//如果连通分量个数不为1，则不是连通图 
}
void dfs(int k)//管k是否亮
{if(k > 7){if(check())ans++;return;}dfs(k+1);sel[k] = true;dfs(k+1);sel[k] = false; 
} 
int main()
{initGraph();dfs(1);cout << ans;return 0;
}