这节总结一下优先队列的常用实现方法。

一、基本概念

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （largest-in，first-out）的行为特征。

抽象数据类型：

优先队列的接口同前面讲到的队列的接口一样，是其基于泛型的API接口代码如下：

public interface Queue {//队列是否为空boolean isEmpty();//队列的大小int size();//入队void enQueue(E element);//出队E deQueue();
}

二、基于数组实现的优先队列

实现优先队列最简的方法就是基于前面讲到的基于数组的栈的代码，只需对插入或删除操作作相应的更改即可。

1、基于有序数组的实现

在栈的代码的插入方法中添加代码，将所有较大的元素向右移动一格，以保证数组有序（和插入排序相同），这里我们可以使用二分查找的方法来找出元素应插入的位置，然后再移动元素。这样最大元素，总是在数组的最右边，其删除操作和栈的实现中一样。

代码：

/*** 基于有序数组的实现的优先队列* @author Alent* @param */
public class PriorityQueue> implements Queue{private E[] elements;private int size=0;@SuppressWarnings("unchecked")public PriorityQueue() {elements = (E[])new Comparable[1]; }@Override public int size() {return size;}@Override public boolean isEmpty() {return size == 0;}@Overridepublic void enQueue(E element) {if(size == elements.length) {resizingArray(2*size);//若数组已满将长度加倍}elements[size++] = element;insertSort(elements);}@Overridepublic E deQueue() {E element = elements[--size];elements[size] = null;     //注意：避免对象游离if(size > 0 && size == elements.length/4) {resizingArray(elements.length/2);//小于数组1/4,将数组减半}return element;}//插入排序，由于前面n-1个元素是有序的，这里只插入最后一个元素public void insertSort(E[] a) {int N = size -1; //最后一个元素是size-1，不是a.length-1if(N == 0) return;int num = binaryFind(a, a[N], 0, N-1);E temp = a[N];//num后的元素向后移动for (int j = N; j > num; j--) {a[j] = a[j-1];}a[num] = temp;}//找出元素应在数组中插入的位置public int binaryFind(E[] a, E temp, int down, int up) {if(upa.length || down<0) {System.out.println("下标错误");}if(temp.compareTo(a[down]) < 0) return down;if(temp.compareTo(a[up]) > 0) return up+1;int mid = (up-down)/2 + down;if(temp.compareTo(a[mid]) == 0) {return mid + 1;}else if(temp.compareTo(a[mid])<0) {up = mid-1;}else if(temp.compareTo(a[mid])>0) {down = mid+1;}return binaryFind(a,temp,down,up);}//交换两个元素public void swap(E[] a,int i,int j) {E temp = a[i];a[i] = a[j];a[j] = temp;}//调整数组大小public void resizingArray(int num) {@SuppressWarnings("unchecked")E[] temp = (E[])new Comparable[num];for(int i=0;itemp[i] = elements[i];}elements = temp;}public static void main(String[] args) {int[] a = {4,2,1,3,8,new Integer(5),7,6};//测试数组PriorityQueue pq = new PriorityQueue();System.out.print("入栈顺序：");for(int i=0;iSystem.out.print(a[i]+" ");pq.enQueue(a[i]);}System.out.println();System.out.print("出栈顺序数组实现：");while(!pq.isEmpty()) {System.out.println(pq.deQueue());}}
}

2、基于无序数组的实现

同样，我们一个可以在删除方法中修改，在删除方法中添加一段类似于选择排序内循环的代码，每次删除时先找出数组中的最大元素，然后与最右边元素进行交换，然后在删除元素。

代码：

@Override
public void enQueue(E element) {if(size == elements.length) {resizingArray(2*size);//若数组已满将长度加倍}elements[size++] = element;
}@Override
public E deQueue() {swapMax(elements);E element = elements[--size];elements[size] = null;     //注意：避免对象游离if(size > 0 && size == elements.length/4) {resizingArray(elements.length/2);//小于数组1/4,将数组减半}return element;
}public void swapMax(E[] a) {int max = size -1;for(int i=0;iif(larger(a[i],a[max])) max = i;}swap(a, size-1, max);
}//比较两个元素大小
public boolean larger(E a1, E a2) {return a1.compareTo(a2)>0;
}

三、基于堆实现的优先队列

基本概念：

当一个二叉树的每个结点都大于等于它的两个子结点时，我们称它是堆有序的。根结点是堆有序的二叉树的最大结点。

二叉堆是一组能够用堆有序的完全二叉树排序的元素，并在数组中按照层级存储。

一棵堆有序的完全二叉树

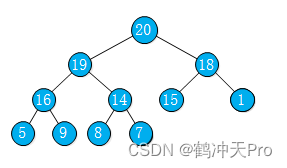
为了操作方便，这是我们使用一个数组，来表示一个堆。我们不使用数组的第一个元素，具体实现在《数据结构与算法（四），树》中有提及，这里就不说了。

1、堆的有序化

当我们将元素插入到堆（数组的末尾）中时，插入的元素可能比它的父结点要大，堆的有序状态被打破。我们需要交换它和它的父节点来修堆，直到堆重新变为有序状态。其操作如下图：

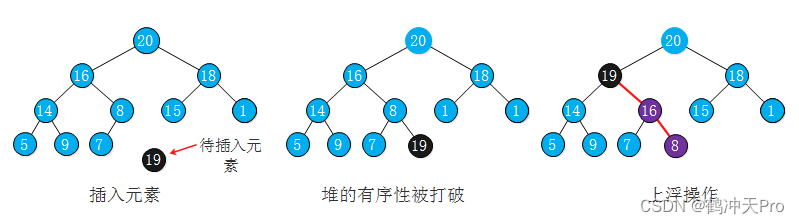
代码如下：

//上浮操作
private void swim(int k) {while(k > 1 && less(k/2, k)) {swap(k/2, k);k = k/2;}}private boolean less(int i, int j) {return elements[i].compareTo(elements[j]) < 0;
}//交换两个元素
public void swap(int i,int j) {E temp = elements[i];elements[i] = elements[j];elements[j] = temp;
}

同样的，当我们从堆中删除根结点并将它的最后一个元素放到顶端时，堆的有序性被打破，我们需要将它与它的两个子结点种的较大者进行交换，以恢复堆的有序性，其操作流程如下图：

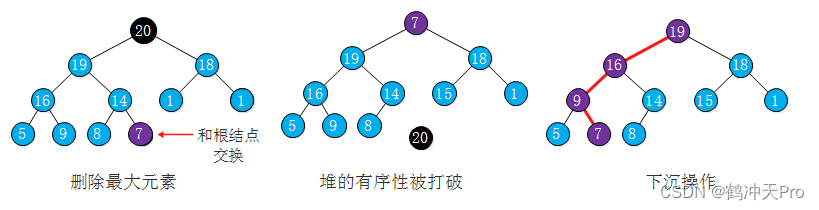
其代码如下：

//下沉操作
private void sink(int k) {while(2*k <= size) {int j = 2*k;if(j < size && less(j, j+1))j++;if(!less(k,j))break;swap(k,j);k = j;}
}

2、基于堆实现的优先队列

基于堆的优先队列的实现代码如下：

/*** 基于堆的优先队列* @author Alent*/
public class MaxPQ> implements Queue{private E[] elements;private int size=0;@SuppressWarnings("unchecked")public MaxPQ(int capacity) {elements = (E[])new Comparable[capacity + 1]; }@Override public int size() {return size;}@Override public boolean isEmpty() {return size == 0;}@Overridepublic void enQueue(E element) {elements[++size] = element;swim(size);}//上浮private void swim(int k) {while(k > 1 && less(k/2, k)) {swap(k/2, k);k = k/2;}}private boolean less(int i, int j) {return elements[i].compareTo(elements[j]) < 0;}@Overridepublic E deQueue() {E result = elements[1];swap(1, size--);elements[size + 1] = null;sink(1);return result;}//下沉private void sink(int k) {while(2*k <= size) {int j = 2*k;if(j < size && less(j, j+1))j++;if(!less(k,j))break;swap(k,j);k = j;}}//交换两个元素public void swap(int i,int j) {E temp = elements[i];elements[i] = elements[j];elements[j] = temp;}
}

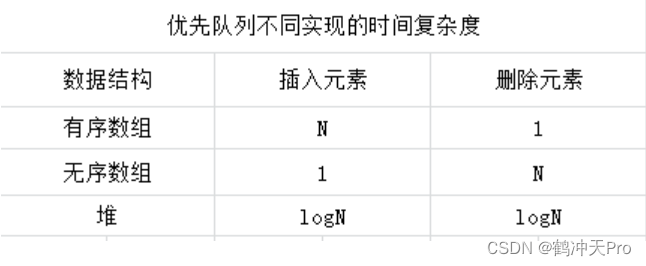
三种实现方法的时间复杂度比较：

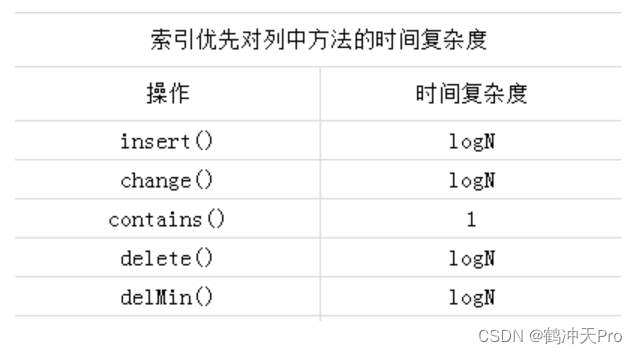
四、索引优先队列

索引优先队列，它用一个索引数组保存了某个元素在优先队列中的位置，使得我们能够引用已经进入优先队列中的元素。最在些应用中，通常是很有必要的，如：有向图的Dijkstra算法中就使用了索引优先队列，来返回最小边的索引。

其实现方法为：

使用elements[]数组来保存队列中的元素，pq[]数组用来保存elements中元素的索引，在添加一个数组qp[]来保存pq[]的逆序——qp[i]的值是i在pq[]中的位置（即 pq[qp[i]] = i）。若i不在队列中，则令qp[i] = -1。辅助函数less()、swap()、sink()、swim()和前面优先队列中的一样。

索引优先队列的代码实现：

/*** 基于堆实现的索引优先队列*/
public class IndexMinPQ>{private int[] pq; //索引二叉堆private int[] qp; // 保存逆序：pq[qp[i]] = i;private E[] elements; //元素private int size = 0;@SuppressWarnings("unchecked")public IndexMinPQ(int capacity) {elements = (E[]) new Comparable[capacity + 1];pq = new int[capacity + 1];qp = new int[capacity + 1];for (int i = 0; i <= capacity; i++) {qp[i] = -1;}}public boolean isEmpty() {return size == 0;}//删除最小元素，并返回索引public int delMin() {int index = pq[1];swap(1, size--);sink(1);elements[pq[size + 1]] = null;qp[pq[size + 1]] = -1;return index;}//删除索引k及其元素public void delete(int k) {int index = qp[k];swap(index, size--);swim(index);sink(index);elements[k] = null;qp[k] = -1;}//插入元素，将它和索引k关联public void insert(int k, E element) {size++;qp[k] = size;pq[size] = k;elements[k] = element;swim(size);}//改变索引k关联的元素public void change(int k, E element) {elements[k] = element;swim(qp[k]);sink(qp[k]);}//是否包含索引kpublic boolean contains(int k) {return qp[k] != -1;}//下沉private void sink(int k) {while (2 * k <= size) {int j = 2 * k;if (j < size && less(j, j + 1))j++;if (!less(k, j))break;swap(k, j);k = j;}}//上浮private void swim(int k) {while (k > 1 && less(k / 2, k)) {swap(k, k / 2);k = k / 2;}}private boolean less(int i, int j) {return elements[pq[i]].compareTo(elements[pq[j]]) > 0;}//交换两元素private void swap(int i, int j) {int swap = pq[i];pq[i] = pq[j];pq[j] = swap;qp[pq[i]] = i;qp[pq[j]] = j;}
}

索引优先队列的时间复杂度：