推荐系统-基于领域的协同过滤算法选择(一文足矣)
1、基于用户的协同过滤算法(UserCF)
1.1、 基本思想
该算法主要用于计算两个用户之间的相似度,这里的相似度指的是两个用户之间的兴趣相似度。假设存在用户u和用户v,N(u)和N(v)分别是他们曾经有过正反馈的物品的集合,那么可以通过Jaccard相似系数公式来计算u和v的相似度:
Wuv=∣N(u)⋂N(v)∣∣N(u)⋃N(v)∣\ W_{uv} = \frac{\left\rvert N(u) \bigcap N(v) \right\lvert}{\left\rvert N(u) \bigcup N(v) \right\lvert} Wuv=∣N(u)⋃N(v)∣∣N(u)⋂N(v)∣
或通过余弦相似度来计算他们之间的相似度:
Wuv=∣N(u)⋂N(v)∣∣N(u)∣∣N(v)∣W_{uv} = \frac{\left\rvert N(u) \bigcap N(v) \right\lvert}{\sqrt{\left\rvert N(u) \right\lvert \left\rvert N(v) \right\lvert}} Wuv=∣N(u)∣∣N(v)∣∣N(u)⋂N(v)∣
例如:假设用户U1对物品 {a, b, d}有过行为记录,用户U2对物品{a,c,f}有过行为记录,那么通过余弦相似度来计算U1和U2之间的相似度为:
wAB=∣{a,b,d}⋂{a,c,f}∣∣{a,b,d}∣∣{a,c,f}∣w_{AB} = \frac{\left\rvert \{a,b,d\} \bigcap \{a,c,f\} \right\lvert}{\sqrt{\left\rvert \{a,b,d\} \right\lvert \left\rvert \{a,c,f\} \right\lvert}} wAB=∣{a,b,d}∣∣{a,c,f}∣∣{a,b,d}⋂{a,c,f}∣
=∣1∣∣3∣∣3∣=\frac{\left\rvert 1 \right\lvert}{\sqrt{\left\rvert 3 \right\lvert \left\rvert 3 \right\lvert}} =∣3∣∣3∣∣1∣
=13= \frac{1}{3} =31
1.2、计算效率提高
以上方法需要计算两两用户之间的相似度,复杂度为 O(∣U∣2)O(\left\rvert U \right\lvert^2)O(∣U∣2)。当用户数量很多时,此方法非常耗时,特别是当大量用户之间相关性较低时(即∣N(u)⋂N(v)∣\left\rvert N(u) \bigcap N(v) \right\lvert∣N(u)⋂N(v)∣为0时),对这些用户的计算是完全不需要的。因此,我们只需先判断∣N(u)⋂N(v)∣\left\rvert N(u) \bigcap N(v) \right\lvert∣N(u)⋂N(v)∣是否为0,然后为非零的用户之间计算相似度即可。
AabdBacfCacdDbd(1.1)\begin{matrix} A & a & b & d \\ B & a & c & f \\ C & a & c & d \\ D & b & d \end{matrix} \tag{1.1} ABCDaaabbccddfd(1.1)
对于矩阵(1.1)^{(1.1)}(1.1),首先建立从物品到用户之间的二维倒排表,每一个物品都在该表中占据一行。对于表的每一行,首个元素是一个物品,如果某用户u对该物品产生过行为记录,则将u加入到该行中。对于每一行的用户列表,其内的用户两两之间都存在着相似性。
aABCbADcBCdACDfB(1.2)\begin{matrix} a & A & B & C \\ b & A & D \\ c & B & C \\ d & A & C & D \\ f & B \end{matrix} \tag{1.2} abcdfAABABBDCCCD(1.2)
然后,建立∣U∣×∣U∣\left\rvert U \right\lvert \times \left\rvert U \right\lvert∣U∣×∣U∣的稀疏矩阵C,如果用户u和用户v同时在倒排表的k行中都出现过,那说明u和v共同对这k个物品产生过行为记录,即C[u][v]= k,初始化时C的各个元素均为0。
ABCDA0000B0000C0000D0000\begin{array}{c|lcr} & \text{A} & \text{B} & \text{C} & \text{D} & \\ \hline A & 0 & 0 & 0 & 0 \\ B & 0 & 0 & 0 & 0 \\ C & 0 & 0 & 0 & 0 \\ D & 0 & 0 & 0 & 0 \\ \end{array} ABCDA0000B0000C0000D0000
遍历二维倒排表(1.2)^{(1.2)}(1.2)的每一行中的用户列表,对其中的任意两个用户u和v,将C[u][v]和C[v][u]加1。这样,遍历完成之后,C[u][v]的值就等于:
ABCDA0122B1020C2201D2010(1.3)\begin{array}{c|lcr} & \text{A} & \text{B} & \text{C} & \text{D} & \\ \hline A & 0 & 1 & 2 & 2 \\ B & 1 & 0 & 2 & 0 \\ C & 2 & 2 & 0 & 1 \\ D & 2 & 0 & 1 & 0 \\ \end{array} \tag{1.3} ABCDA0122B1020C2201D2010(1.3)
可见,矩阵(1.3)^{(1.3)}(1.3)是一个对称矩阵。在计算出了所有用户两两之间的相似度之后,利用UserCF算法会向用户推荐与他兴趣最相近的k个用户最喜欢的物品,如下公式度量了用户u对物品i的感兴趣程度:
p(u,i)=∑v∈S(u,k)⋂N(i)wuvrvip(u,i) = \sum_{v \in S(u,k) \bigcap N(i)}{w_{uv}r_{vi}} p(u,i)=v∈S(u,k)⋂N(i)∑wuvrvi
其中,S(u,k)S(u,k)S(u,k)包含与用户u兴趣最相近的k的用户列表,N(i)是对物品i有过行为的用户列表,wuvw_{uv}wuv是用户u与用户v的兴趣相似度,rvir_{vi}rvi代表用户v对物品i的喜欢程度(由于此处使用的是单一行为的隐反馈数据,因此所有的rvir_{vi}rvi=1)。
1.3、算法参数说明
参数k是UserCF算法的最重要参数,它对推荐算法的各种指标都会产生一系列影响:
- 精度(准确率和召回率):准确率和召回率与参数k并不呈线性关系,但是选择合适的k对于获得推荐系统高的精度比较重要;
- 流行度:当k越大,则UserCF推荐的物品就越热门;
- 覆盖率:当k越大,流行度就越大,相反,覆盖率会相应地越小。
1.4 改进UserCF-IIF 算法
首先,以飞天茅台为例,如果两个用户都曾经买过“飞天茅台”,这丝毫不能说明他们兴趣相似, 因为绝大多数中国人过春节时都买过“飞天茅台”。但如果两个用户都买过“茅乡酒”,那可以认为他们的兴趣比较相似,因为只有买“茅乡酒”的人才会买飞天茅台。换句话说,两个用户对冷门物品采取过同样的行为更能说明他们兴趣的相似度。
因此,John S. Breese在论文1中提出了 如下公式(UserCF-IIF),根据用户行为计算用户的兴趣相似度:
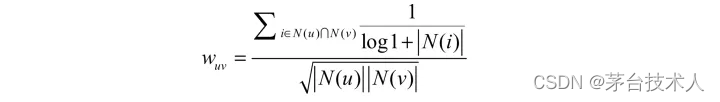

UserCF-IIF在各项性能上略优于UserCF,这说明在计算用户兴趣相似度时考虑物品的流行度对提升推荐结果的质量确实有帮助。
基于用户的协同过滤算法的天然缺点:
- 随着网站的用户数目越来越大,计算用户兴趣相似度矩阵将越来越困难,其运算时间复杂度和空间复杂度的增长和用户数的增长近似于平方关系;
- 基于用户的协同过滤很难对推荐结果作出解释。
2、基于物品的协同过滤算法(ItemCF)
2.1、基本思想
该算法向用户推荐与他们之前喜欢的物品相似的其他物品。例如,如果你购买过"茅乡酒”,会向你推荐“飞天茅台”。
ItemCF算法通过计算用户的历史行为记录,来计算物品之间的相似度,如果喜欢物品A的用户大多数也喜欢物品B,那么认为物品A与物品B具有一定的相似度,这就很容易为推荐结果做出合理的解释。
假设,N(A)和N(B)分别是喜欢物品A和物品B的用户数量, ∣N(A)⋂N(B)∣\left\rvert N(A) \bigcap N(B) \right\lvert∣N(A)⋂N(B)∣是既喜欢A又喜欢B的用户的数量,那么物品A和物品B的相似度为(喜欢A的用户中有多少人也喜欢B):
wAB=∣N(A)⋂N(B)∣∣N(A)∣(2.1)w_{AB} = \frac{\left\rvert N(A) \bigcap N(B) \right\lvert}{\left\rvert N(A) \right\lvert} \tag{2.1} wAB=∣N(A)∣∣N(A)⋂N(B)∣(2.1)
公式存在热物品问题:如果B是个很热门的商品,那么将会接近于1(因为喜欢A的人都喜欢B),这会造成任何其他物品与某个热门物品都很相似。因此,我们对公式作一些修改,加上一个惩罚物品B的权重因子,得到了公式:
wAB=∣N(A)⋂N(B)∣∣N(A)∣∣N(B)∣(2.2)w_{AB} = \frac{\left\rvert N(A) \bigcap N(B) \right\lvert}{\sqrt{\left\rvert N(A) \right\lvert \left\rvert N(B) \right\lvert}} \tag{2.2} wAB=∣N(A)∣∣N(B)∣∣N(A)⋂N(B)∣(2.2)
2.2、计算过程
假设物品的全集是I,首先建立一个∣I∣×∣I∣\left\rvert I \right\lvert \times \left\rvert I \right\lvert∣I∣×∣I∣的全零矩阵C(2.3)^{(2.3)}(2.3)
abcdfa00000b00000c00000d00000f00000(2.3)\begin{array}{c|lcr} & \text{a} & \text{b} & \text{c} & \text{d} & \text{f} \\ \hline a & 0 & 0 & 0 & 0 & 0 \\ b & 0 & 0 & 0 & 0 & 0 \\ c & 0 & 0 & 0 & 0 & 0 \\ d & 0 & 0 & 0 & 0 & 0 \\ f & 0 & 0 & 0 & 0 & 0 \\ \end{array} \tag{2.3} abcdfa00000b00000c00000d00000f00000(2.3)
得到(2.4)^{(2.4)}(2.4)中的用户-物品兴趣列表:
AabdBacfCacdDbd(2.4)\begin{matrix} A & a & b & d \\ B & a & c & f \\ C & a & c & d \\ D & b & d \end{matrix} \tag{2.4} ABCDaaabbccddfd(2.4)
如果物品对(x,y)(x, y)(x,y)出现某个用户的兴趣列表中,则将C[y][x]和C[x][y]都加1,如此遍历(2.4)^{(2.4)}(2.4)之后,得到了最终的相似矩阵C:
abcdfa01221b10020c20011d22100f10100(2.5)\begin{array}{c|lcr} & \text{a} & \text{b} & \text{c} & \text{d} & \text{f} \\ \hline a & 0 & 1 & 2 & 2 & 1 \\ b & 1 & 0 & 0 & 2 & 0 \\ c & 2 & 0 & 0 & 1 & 1 \\ d & 2 & 2 & 1 & 0 & 0 \\ f & 1 & 0 & 1 & 0 & 0 \\ \end{array} \tag{2.5} abcdfa01221b10020c20011d22100f10100(2.5)
在得到两两物品之间的相似度后,ItemCF通过公式(2.6)^{(2.6)}(2.6)来计算用户u对物品i的兴趣。
假设N(u)是用户喜欢的物品集合,S(i,K)是与物品i最相似的K个物品的集合,wijw_{ij}wij是物品i与物品j的相似度,rujr_{uj}ruj是用户u对物品j的兴趣(对于隐反馈数据集,如果用户u对物品j产生过行为,则可令rujr_{uj}ruj=1),puip_{ui}pui是用户u对物品i的兴趣,那么:
pui=∑j∈N(u)⋂S(i,k)wijruj(2.6)p_{ui} = \sum_{j \in N(u) \bigcap S(i,k)}{w_{ij} r_{uj}} \tag{2.6} pui=j∈N(u)⋂S(i,k)∑wijruj(2.6)
2.3、算法参数说明
参数K是ItemCF算法的最重要参数,它对推荐算法的各种指标都会产生一些列的影响:
- 精度(准确率和召回率):准确率和召回率与参数k并不呈正相关或者负相关,但是选择合适的K对于获得推荐系统高的精度比较重要;
- 流行度:随着K的增大,推荐结果的流行度会逐渐提高,但是当K增加到一定的程度,流行度就不会再有明显变化;
- 覆盖率:当K越大,覆盖率会相应地降低。
2.4、改进ItemCF-IUF算法
用户活跃度对物品相似度的影响:在ItemCF中,两个物品之间能产生相似度是因为它们共同出现在了多个用户的兴趣物品列表中,因此用户会对其兴趣列表中的两两物品的相似度产生贡献。但是,不同的用户的贡献是不相同的。
例如,图书馆管理员买了京东上90%的图书,但绝大部分都不是他的兴趣;而一个文艺青年买了5本小说,但都是他的兴趣。所以,图书管理员对他所买的书的两两相似度,要远远小于文艺青年。
因此,活跃的用户,相比起不活跃的用户而言,对物品之间相似度的贡献更小。John S. Breese在论文中提出了IUF(Inverse User Frequence)的概念。假设N(u)是用户u喜欢的物品列表,那么用户u的IUF参数为:
1log(1+∣N(u)∣)(2.7)\frac{1}{log(1+\left\rvert N(u) \right\lvert)} \tag{2.7} log(1+∣N(u)∣)1(2.7)
增加了IUF参数的物品相似度公式为:
wAB=∑u∈N(A)⋂N(B)1log(1+∣N(U)∣)∣N(A)∣∣N(B)∣(2.8)w_{AB} = \frac{\sum_{u \in N(A) \bigcap N(B)}{\frac{1}{log(1+\left\rvert N(U) \right\lvert)}}} {\sqrt{\left\rvert N(A) \right\lvert \left\rvert N(B) \right\lvert}} \tag{2.8} wAB=∣N(A)∣∣N(B)∣∑u∈N(A)⋂N(B)log(1+∣N(U)∣)1(2.8)
算法(2.8)^{(2.8)}(2.8)记为 ItemCF-IUF。实际上,对于过于活跃的用户,例如上面的图书管理员,一般直接忽略其兴趣物品列表,不将其纳入到相似度计算的数据集中。
2.5、物品相似度的归一化处理
Karypis在论文中提到:在ItemCF中,如果将相似度矩阵按照最大值进行归一化处理(将最大值设为1行不行?),那么可以提高推荐的准确率:
wij′=wijmaxjwijw_{ij}^{'} = \frac{w_{ij}}{\max_{j}{w_{ij}}} wij′=maxjwijwij
除了提高推荐结果的准确率外,归一化还能够提高推荐结果的覆盖率和多样性。
举例
假设有两类物品A和B,A类物品之间的相似度为0.5,B类物品之间的相似度为0.6,A类物品和B类物品之间的相似度为0.2。在这种情况下,如果某用户喜欢5个A类物品和5个B类物品,那么ItemCF算法会向该用户推荐B类物品,因为B类物品之间的相似度比较大。对相似度进行归一化处理后,A类物品之间的相似度变成了1,B类物品之间的相似度也是1,在这种情况下,如果用户喜欢5个A类物品和5个B类物品,那么系统向他推荐的A类物品和B类物品的数量应该是大致相等的。
什么样的品类其类内物品之间的相似度较高,什么样的品类其类内物品之间的相似度较低?
一般来说,越是热门的类,其类内物品的相似度越大,如果不进行归一化,那么就会倾向于推荐热门类里的物品,造成推荐的覆盖率低。
2.6、ItemCF算法的缺陷
上面提到越是热门的品类,其品类内物品的相似度越大。除此之外,不同领域的最热门物品之间的相似度往往也是很高。
举例
老一辈人喜欢看新闻联播,不看其他新闻节目。他们在看完新闻联播后,立刻换台去看中央8套的国产电视剧,其他电视剧(如偶像剧)几乎不看。那么,通过ItemCF算法得到的数据,我们很容易认为新闻联播与黄金时段的电视剧的相似度很高,而新闻联播与其他新闻节目(如广州时政要闻)的相似度很低,这显然是不合理的。
对于这类问题,仅仅靠用户数据是不能解决的,必须引入物品的内容数据。这超出了协同过滤的范围。
3、UserCF VS ItemCFU
UserCF和ItemCF算法在实际场景中的应用:
| 公司 | 算法 | 用途 |
|---|---|---|
| Digg | UserCF | 个性化网络文章推荐 |
| GroupLens | UserCF | 个性化新闻推荐 |
| NetFlix | ItemCF | 电影推荐 |
| Amazon | ItemCF | 购物推荐 |
为什么新闻推荐使用UserCF算法,而购物网站使用ItemCF算法?
UserCF算法的推荐结果着重于反映那些与目标用户兴趣相似的小群体的热点,而ItemCF算法的推荐结果着重于维护目标用户的历史兴趣。换句话说,UserCF的推荐更加社会化,而ItemCF的推荐更加个性化。
3.1、UserCF与ItemCF算法的比较
| 类比 | UseCF | ItemCF |
|---|---|---|
| 性能 | 适合于用户数量较小的场景,如果用户很多,则计算用户之间相似度矩阵的代价很大 | 适用于物品数量明显小于用户数量的场景,如果物品很多,则计算物品之间相似度矩阵的代价很大 |
| 领域 | 时效性较强,用户个性化兴趣不太明显的领域 | 适长尾物品丰富,用户个性化需求强烈的领域 |
| 实时性 | 用户的新行为不一定导致推荐结果的立即变化 | 适用户的新行为一定会导致推荐结果的实时变化 |
| 冷启动 | 当新用户对很少量的物品产生行为后,不能立即对他进行推荐,因为用户相似度表一般是每隔一段时间离线计算的。当新物品上线后,一旦有某个用户对该物品产生行为,就可以将该物品推荐给与该用户相似的其他用户 | 新用户只要对一个物品产生行为,就可以向他推荐与该物品相似的其他物品必须在更新了物品相似度表(离线)之后,才能将新的物品推荐给其他用户 |
| 推荐理由 | 很难提供令用户信服的推荐解释 | 利用用户的历史行为来作为推荐理由,容易令用户信服 |